持续运行下机械加工制造的综合误差控制技术研究

赵 岩

(河南工业职业技术学院机械工程学院，河南 南阳 473000)

机械加工方法是使用机械对材料进行切、磨、削等加工的方法，它是产品革新的一种重要手段。经济全球化对制造企业的响应能力和产品质量提出了更高的要求，需要企业不断地提高产品的加工质量和生产效率，并且降低废品率和加工成本，因此企业对相关技术的研发给予了高度的重视，例如加工制造过程的监控和保障技术的研究开发[1-2]。在机械加工制造过程中，只有将制造误差降到最低，才能在最大程度上提高制造精度，继而推进企业的快速发展[3]。

文献[4]在分析国内外磨削加工误差与补偿问题时，提出一种轮廓误差分析和补偿策略，针对的是X轴和C轴两轴联动的凸轮轴数控磨削的轮廓误差。文献[5]针对零件加工精度原位检测系统的检测精度问题，对残余误差的回归进行建模和补偿，完成对曲面零件测点法矢方向检测数据的二次补偿。但以上方法在机械持续运行的环境下无法对加工过程中的误差进行有效控制。

为此，本文提出持续运行下机械加工制造的综合误差控制技术，引入数据融合技术以及线性插补技术，完成对机械加工制造综合误差的有效控制。

1 持续运行下机械加工制造误差计算过程

1.1 约束条件建立

在机械加工制造过程中，平稳运行情况下的机械加工精度为一固定值[6]，而当运行情况发生变化时，其加工精度会发生变化，加工精度误差的变化规律完全符合离散分布函数特性，则持续运行下加工精度的误差Er可以表达为：

(1)

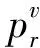
在机械生产过程中，每一个生产周期内都需要对加工的精度及加工的时间进行误差控制，此误差直接由加工任务的性质决定[7-8]。持续运行加工过程中，生产周期产生的误差主要有两个来源：一是任务加工形成的误差，二是辅助生产设备产生的误差。任务加工形成的误差主要是由于在加工前和加工过程中机床、夹具、刀具和工件所组成的工艺系统存在很多的误差因素造成的；辅助生产造成的误差主要是由生产辅助系统造成的。用时间维分析模型可以分析持续运行下两种误差，则该模型可表示为：

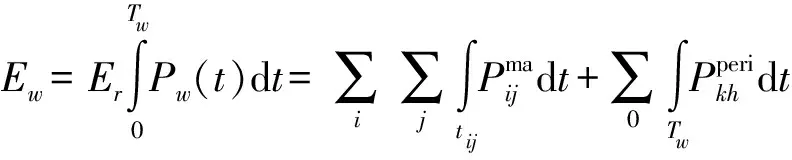
(2)

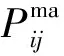
(3)

(4)

式中：Nmin为持续运行情况下机床主轴运行中可通过的最小转速；D为刀具直径，vc为铣削速度，fz为每齿进给量;vmin为持续运行情况下机床允许的最低进给速度;z为机械设备耗能参数。

1.2 持续运行下机械加工制造误差数值计算

在持续运行下，除电机外，机床的其他设备也存在持续运行造成误差的风险，需要考虑持续运行下机械加工制造的主轴电机及进给轴产生的误差[11]。在忽略电机种类的情况下，只考虑电机工作原理，电机产生误差Pm公式如下：

(5)

式中：PCu,PFe分别为铜材料及铁材料配比误差；Pad为机械误差；Pmec为附加载荷误差；Ek为电动机转子的精度。

对于传动系统的第i节传动环节而言，产生的加工误差是由用于持续传动的主轴电机造成的，而造成主轴电机加工误差产生的原因是持续运行下机械温度过高。第i个进给电机的误差Pi公式如下：

(6)

其中：

(7)

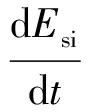
2 持续运行下机械加工制造误差综合控制技术

2.1 机械加工制造误差评估

考虑到约束因素，对持续运行下机械加工制造误差进行计算，为保障机械顺利运行，对该计算结果进行评估，持续运行下的机械加工制造设备安装了若干个进给电机[12-13]，设置进给电机数量为m，其进给电机误差Cfeed为：

(8)

式中：tfsi为开始运行时间；tfei为结束运行时间。

在持续运行下机械加工制造过程中产生的误差重点与相关材料配比有关，从主轴电机到刀具/工件的选择类型可知，主设备误差Cspindle能够进一步分为维持主设备运行的传动模块误差Cm和用于工件材料类型选取的误差Cc。

(9)

式中：Pm为维持主设备运行的传动模块产生的功率;Pc为切削功率;tms和tme分别为主设备开始运行时间及运行终止时间;tcs和tce分别为附加设备开始运行时间及运行结束时间。换刀电机误差与接受换刀的刀具转台架构产生的误差Ctool可以表示为：

Ctool=Ptool·ttool

(10)

式中：Ptool为换刀电机的功率；ttool为转台旋转的时间。

(11)

式中：pos0为转台初始位置；posa为刀具摆放位置；numpos为转台刀架数量；ntool为转台转速。

持续运行的机械加工中机床设备误差为整体误差总和，机床设备误差总和Ctotal评估结果可表示为：

Ctotal=Cspindlem+Cfeed+Ctool+Ccool+Cfix

(12)

式中：Cspindlem为主轴电机误差评估值；Ccool为冷却泵电机误差评估值；Cfix为基础误差评估值。

综上所述，若Ctotal≥1，则误差计算结果合格；若Ctotal<1，则误差计算结果不合格，需要根据误差偏离数值，对计算结果进行补偿。

2.2 持续运行下机械加工制造综合误差控制技术

本文以评估持续运行下机械加工制造误差计算结果为基础，通过线性插补技术，获取误差的偏离数值，引入数据融合技术，根据误差偏离数值对误差评估结果进行补偿，实现对持续运行下机械加工制造综合误差的控制。

1)线性插补技术。

持续运行下机械加工制造过程中误差和刀具路径、各轴进给时间及进给速度有关，可通过伺服差值来管制，其中插补位置与进给速度存在线性变化关系，其变化曲线如图1所示。

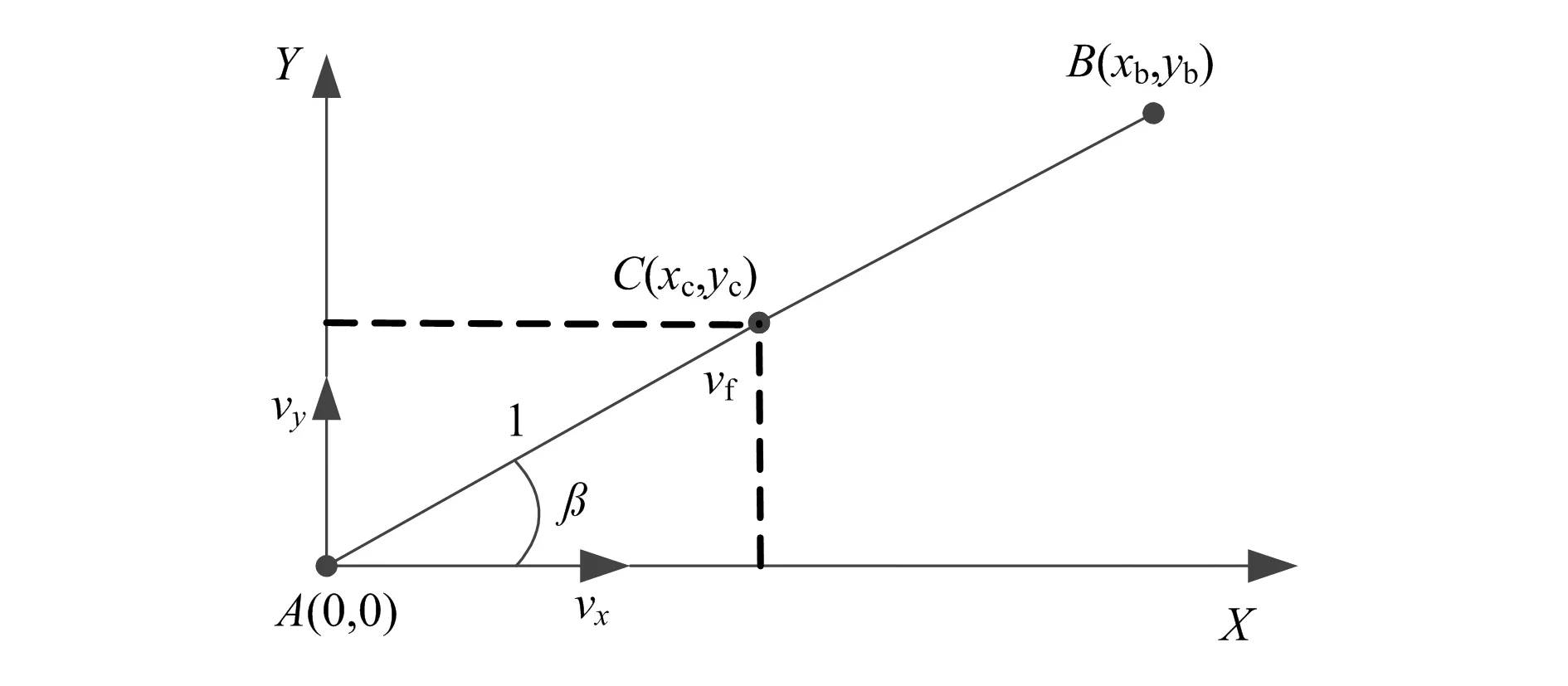
图1 插补位置与速度之间变化曲线

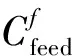
(13)

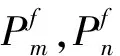
(14)

式中：pservo,pfan分别为伺服系统和电机的误差；(ts-tf)为在整个机械加工制造过程中设备的运行时间。

持续运行下单个机械加工制造设备产生的误差eg公式如下：

(15)

式中：C1为单个设备误差；G为持续运行期间特定时间周期内的有效误差。持续运行下机械加工制造设备整体误差与生产所需误差量、辅助生产设备误差量、附属设备误差量有关，各误差量要以实际情况为准，整体误差偏离数值C计算式为：

(16)

式中：n为误差种类数量；ej为第j种误差；Pj为第j种误差折算量。

2)数据融合技术。

通过数据融合技术，对C进行补偿[14]，并将其与补偿有关的参数，一起输入到数据融合过程设定的参数界面。本文主要针对丝杠和主轴产生的误差进行融合补偿。研究表明，多元回归模型能够较好地描述机械数据融合过程，数据融合过程曲线如图2所示。

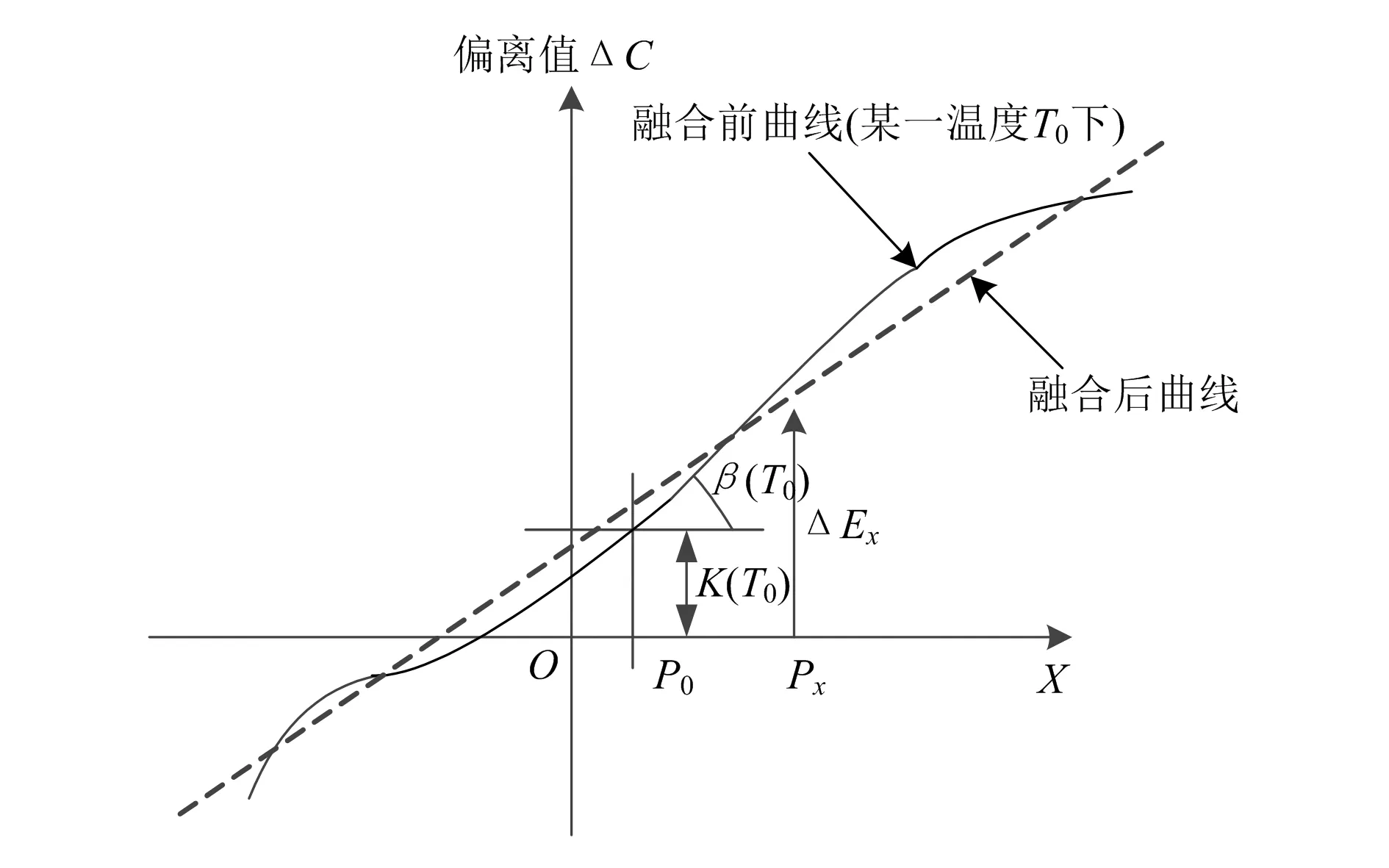
图2 数据融合过程曲线图

图2中，在某一误差下，机械数据融合为一条直线，误差随补偿点坐标Px和融合参考点坐标P0的间隔转变而发生改变。对偏离值进行融合补偿，即对拟合直线误差实施补偿[15]。由此得到数据融合结果Comp为：

Comp=-K(T0)-tan[β(T0)]×(Px-P0)

(17)

式中：K(T0)为数据融合偏置值；tan[β(T0)]为数据融合误差补偿系数。

综上所述，给出基于数据融合的机械加工制造综合误差控制流程，如图3所示。

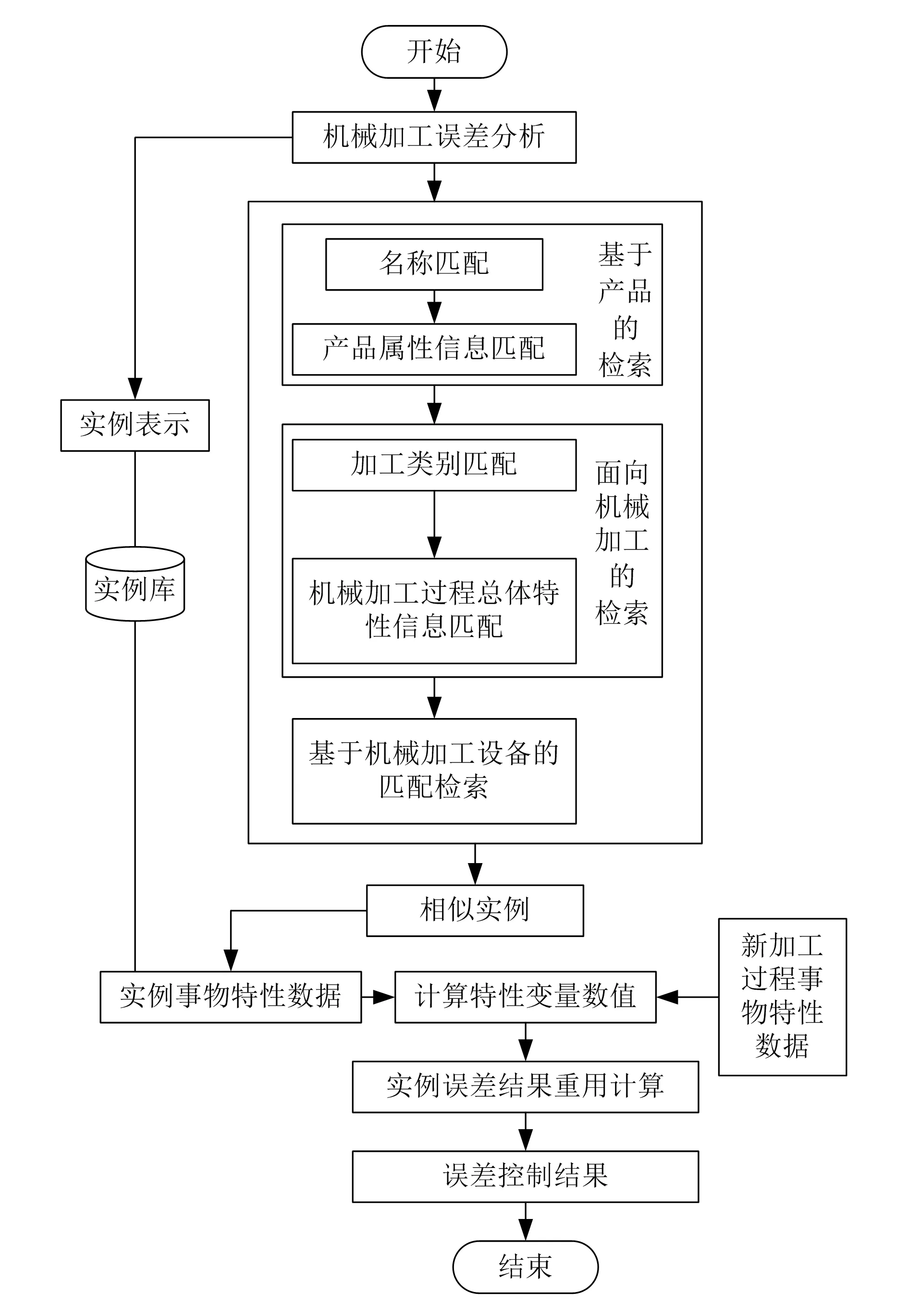
图3 机械加工制造综合误差控制流程图

3 实验结果分析

为了证明所提技术的有效性，下面进行实验验证。实验以C6150/HK卧式车床为对象，实验参数见表1。

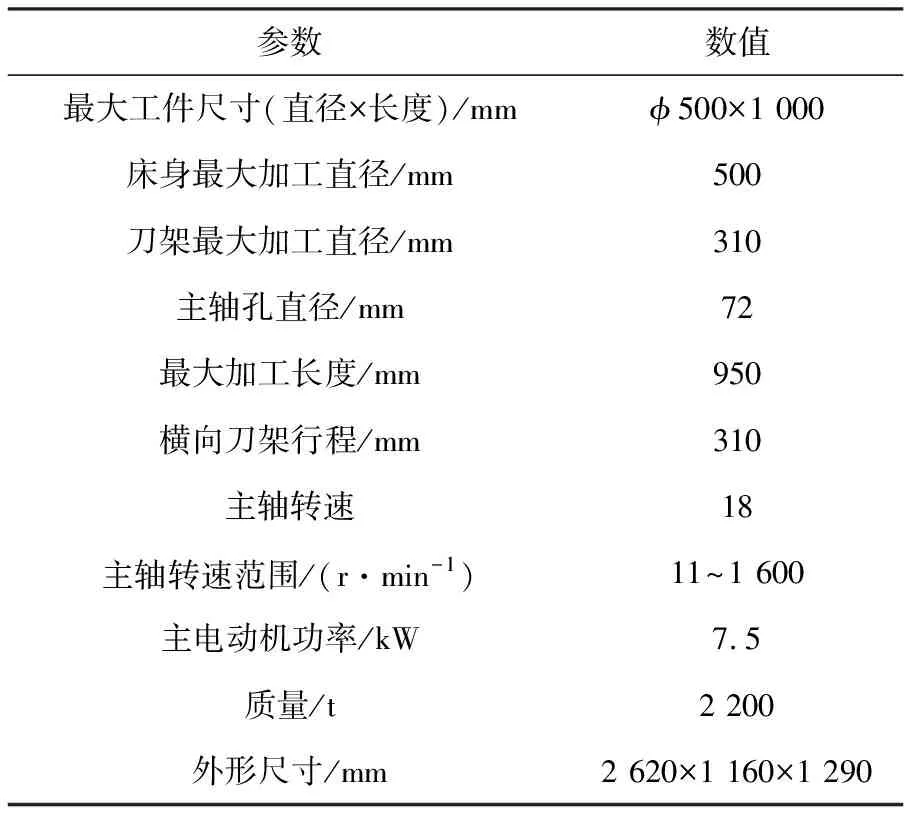
表1 C6150/HK卧式车床实验参数

具体实验步骤如下：

1)在机床上安装应变片扭矩传感器；

2)根据扭矩变化，确定机床的切削力以及转速；

3)根据机床的切削力和转速，得到机械误差Pad;

4)确定Pad与切削时间的关系，验证所提方法的可应用性，如图4所示。

5)验证综合误差控制的准确性。

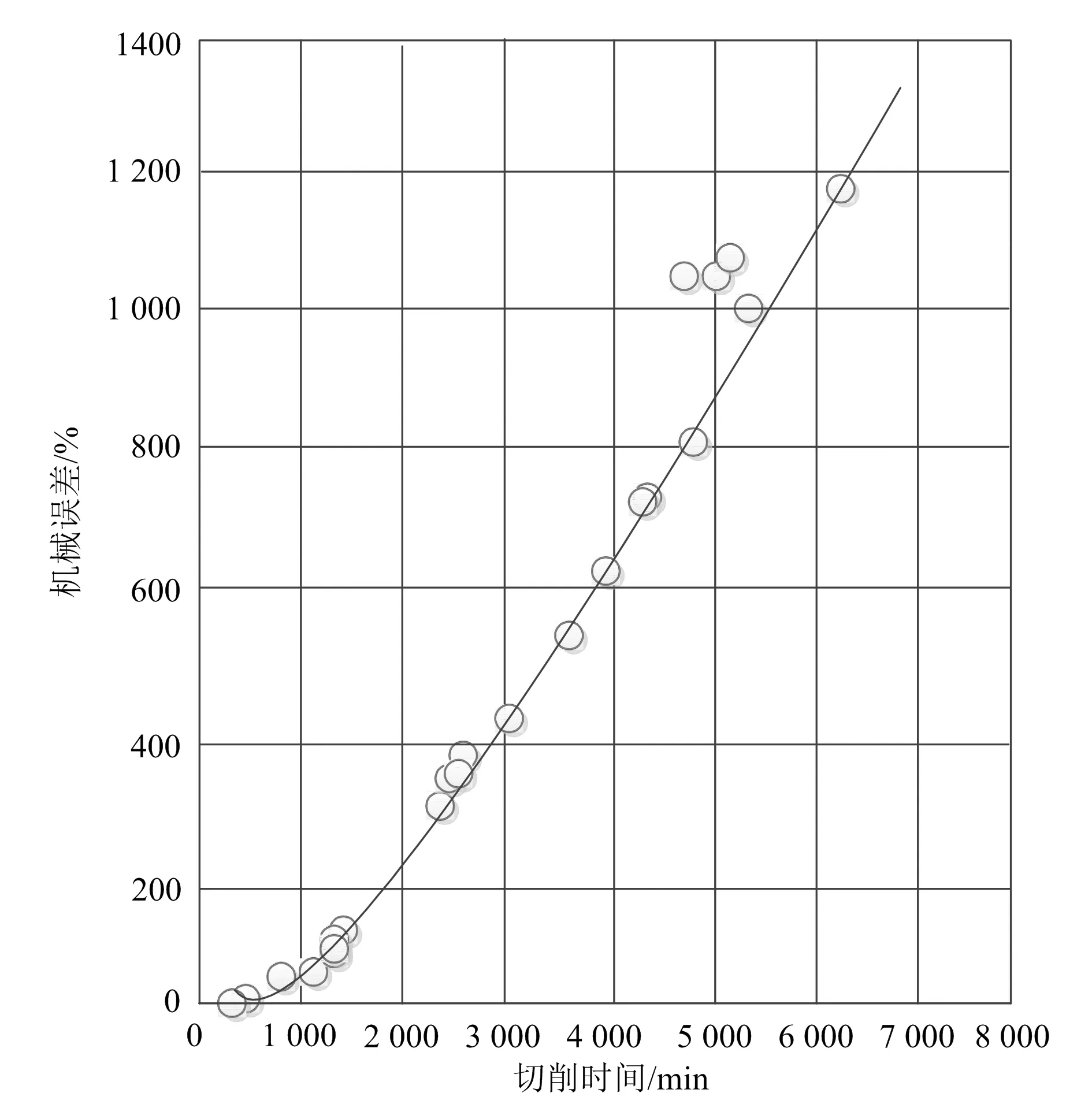
图4 机械误差与切削时间之间关系曲线

图4中的圆圈表示实验得到的机械误差值。由图可知，机械误差为切削时间的二次函数拟合，机械误差系数α是切削时间的一元函数拟合系数，Pc为切削功率，对于机械加工制造过程而言，可得如下函数关系：

(18)

α=1.0×10-5×Pc+0.099

(19)

由式(18)、(19)可知，机械误差与切削时间为函数关系，说明本文所提的综合误差控制技术可提高误差的预测精度，进一步说明该技术具有可应用性。

为了验证所提技术的效果，采用该技术对C6150/HK卧式车床的切削误差进行验证分析。该切割设备的有效切割行程较高，横向的有效切割行程为750mm，纵向的有效切割行程为360mm，最大回转直径为180mm，在切割过程中切割行程会产生一定误差，因此需记录设备的切割误差，实验对比结果如图5所示。

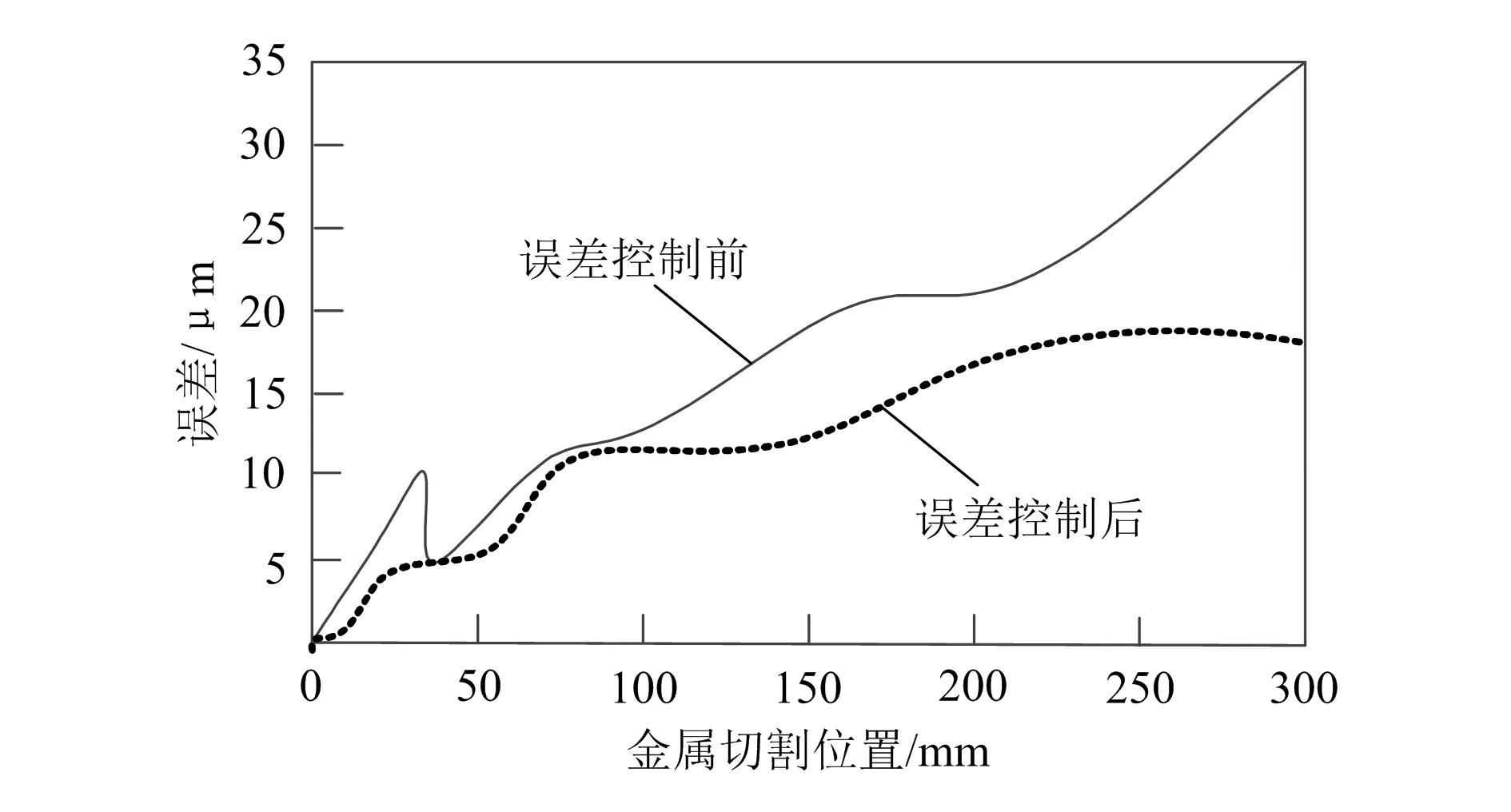
图5 误差控制前后设备切割误差

由图5可以明显看出，利用C6150/HK卧式车床进行金属切割时，切割结果存在误差，传统的设备运行过程中切割误差最高可达35μm，这样的误差值无法满足市场金属零件的精度要求。实验中切割误差最高值为8μm，这说明应用综合误差控制技术能够有效控制设备运行过程中的金属切割误差，验证了持续运行下机械加工制造的综合误差控制的有效性。

4 结束语

本文针对传统机械加工制造过程中的误差控制不够准确的问题，在持续运行环境下，提出一种机械加工制造的综合误差控制技术。通过计算机械加工制造误差数值，结合线性插补技术，计算出误差结果与评估结果之间的偏离数值，并对其进行补偿，完成机械加工制造的综合误差控制。利用C6150/HK卧式车床进行实验，实验结果验证了该技术具有较高的机械加工误差控制精度，有效提高了机械加工效率。