Gumbel分布的参数估计方法探讨
2018-09-21丁咏梅刘丽珺
丁咏梅,刘丽珺,雷 晴
(武汉科技大学 理学院,湖北 武汉 430080)
自然界中的各种非人为灾害通常会采用极值理论去探讨.极值理论的核心就是根据极端事件的极值分布的尾部来建立模型并分析事件的变动特征和预测事件的风险.
极值理论最早追溯到了20世纪早期,冯·博特凯维兹于1922年通过对正态分布的样本极差的研究提出极值问题.此后,Dodd等陆续地展开了极值理论研究.1928年,Fisher提出极值分布的三大类型.1958年,Gumbel出版了著作《Statistics of Extremes》,奠定极值理论的基础[1].近年来,Gumbel分布广泛应用于气象等领域,可有效预测最大降雨量等未知信息.再现期预测的精准度则取决于其参数估计方法的优劣,于是Ahsanullah在1990年和1991年基于记录数据导出了Gumbel分布中位置参数和尺度参数的最大似然估计量和最小方差无偏估计量[2-3].Hong等[4]研究了大样本量时的广义最小二乘法拟合方法及其与其他拟合方法的相比性能在效率、偏差和均方根误差方面的评估.国内,利用Gumbel分布对极端情况变换特征进行研究并运用了PWM,结果表现出较高的拟合优度[5-6].曹兵等[7]在研究设计波高的时候也得出了相似的结论.翟宇梅等[8]运用蒙特卡洛方法选出估计误差最小的经验分布函数从而提出了最优线性矩估计法,认为选择合适的经验分布函数可以提高参数估计的精度.对Gumbel分布进行参数估计时,分别对比不同的估计方法后认为极大似然估计具有较优的稳定表现[9-12].针对我国极端降水量拟合Gumbel分布,发现相比其他参数估计方法,采用L-矩估计法对极端降水量进行拟合优度有着显著的提高[13-15].张延年等[16]采用Gumbel分布对国内最大风速值进行分析和参数估计,发现耿贝尔法比矩法拟合效果好.肖翔等[17]运用比较法和微分法对最小二乘估计量的有效性进行了证明.
基于已有的国内外关于Gumbel分布的参数的估计问题,比较了当前的3种参数估计方法,认为当样本容量较大时,采用MLE能得到更优的结果.考虑到数据的可得性,选择“SpatialExtreme”包中的“rainfall”数据集,对瑞士3个站点的47年极值数据,选择最大似然估计(MLE)、矩法估计(ME)、最小二乘估计(OLS)进行估计分析,并使用优化指标对样本估计值的结果进行比较评价.
1 参数估计
Gumbel分布函数
(1)
式中:μ是位置参数,β>0是尺度参数.不同的位置参数和尺度参数下的Gumbel概率密度函数图像如图1所示.

图1 不同位置参数和尺度参数下的Gumbel概率密度
1.1 矩估计(ME)
Gumbel分布参数的矩估计为:
(2)

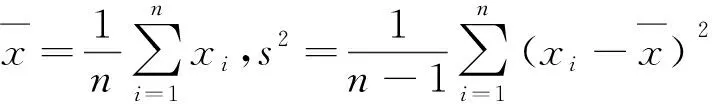
(3)
且估计量的方差
(4)
式中:γ为欧拉常数,ρs=1.139 6,ρk=5.4分别是Gumbel分布的偏度和峰度系数.化简后有
(5)
1.2 最小二乘估计(OLS)
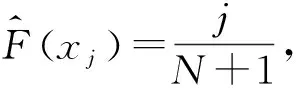
(6)
以残差平方和最小为标准,求u和β的参数估计即实际上即求y与x的回归直线,所以Gumbel分布参数的最小二乘估计量为
(7)
且有
(8)
(9)
由文献[17]可知,该估计具有有效性.易知Gumbel的最小二乘估计具有线性、无偏性及有效性.
1.3 极大似然估计法(MLE)
Gumbel分布对应的概率密度函数
(10)
其中δ>0,-∞ (11) 得似然方程 (12) 由∂lnL/∂θi=0(θ1=β,θ2=u)确定的θi即为极大似然法的估计量.为加快收敛,在设置合适初值的情况下用牛顿迭代法求解. 考虑到数据的可获取性,基于R软件,选择程序包“SpatialExtremes”中数据集“rainfall”中名称为rain的数据,该数据是瑞士的79个不同站点的连续47年的降雨量资料.基于该研究对象,选取了前3个站点连续47的降雨量数据进行分析,简单的统计特征如表1所示. 由站点1的连续47年降雨量数据,基于R语言,得到站点1降雨量所相应的Gumbel分布的3种估计下的结果,如表2所示. 表1 3个站点的统计特征 表2 站点1在3种参数估计方法下的估计结果 类似地,基于R语言,得到站点2降雨量所相应的Gumbel分布的3种参数估计下的结果,如表3所示. 表3 站点2在3种参数估计方法下的估计结果 对于站点2的降雨量分布,得到类似于站点1的统计结果.为了证实在极值分布中,最大似然估计和矩法估计优于最小二乘,选择了站点3作为验证.得到站点3降雨量所相应的Gumbel分布的3种估计办法下的参数估计,如表4所示. 表4 站点3在3种参数估计方法下的估计结果 分位数-分位数图(QQ图)是用于检验数据集的分布假设的有效性的探索性工具,其基本思想是基于所讨论的分布来计算每个数据点的理论预期值,并将变量的有序值与特定理论分布的分位数进行比较,如果数据确实遵循假设分布,即数据确实来自于理论分布,则QQ图上的点将大致落在一条直线上. 本研究分别作出了3站点的降雨量数据在3种参数估计方法下的残差QQ图(图2~图10). 图2 站点1的MLE估计下的残差QQ图 图3 站点1的OLS估计下的残差QQ图 图4 站点1的ME估计下的残差QQ图 图5 站点2的MLE估计下的残差QQ图 图6 站点2的OLS估计下的残差QQ图 图7 站点2的ME估计下的残差QQ图 图8 站点3的MLE估计下的残差QQ图 图9 站点3的OLS估计下的残差QQ图 图10 站点3的ME估计下的残差QQ图 由QQ图可知,OLS对Gumbel分布的估计并不尽如人意.相比之下,ME和MLE下的残差QQ图上的点基本分布在直线附近,效果比较好,特别是ME下的残差QQ图的前一部分的点基本与直线处于重合的状态,显示了非常良好的效果.综合这3个站点的分析结果,在对Gumbel参数的估计中,可以说矩估计和极大似然估计的效果是比较好的,且ME是最优的.而OLS的估计效果可能会因为样本的不同而表现出差异,相比较之下OLS不是最优选择. 作为三大极值分布之一的Gumbel分布,其参数估计在实际应用中具有重要意义.研究通过对Gumbel分布及其参数估计方法的理论分析以及结合了R软件中程序包“SpatialExtremes”中数据集“rainfall”中名称为rain的数据的实证研究,比较了3个站点的适应值函数大小和残差QQ图,不论是从适应值函数的角度,还是从残差QQ图的角度,较最小二乘法,极大似然估计法和矩估计都表现良好.另外,其他还有例如概率加权法、分位数法等参数估计法有待进一步的研究,因此不排除对于Gumbel分布的参数估计还有更加有效的方法的可能性.2 数据来源及其特征分析





3 模型诊断
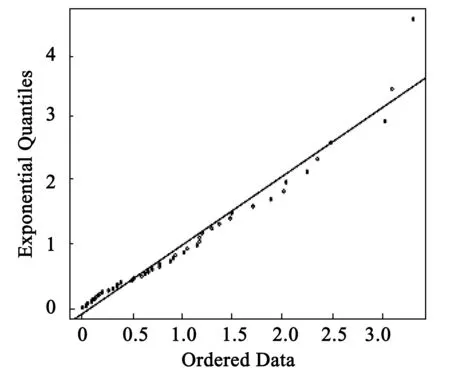
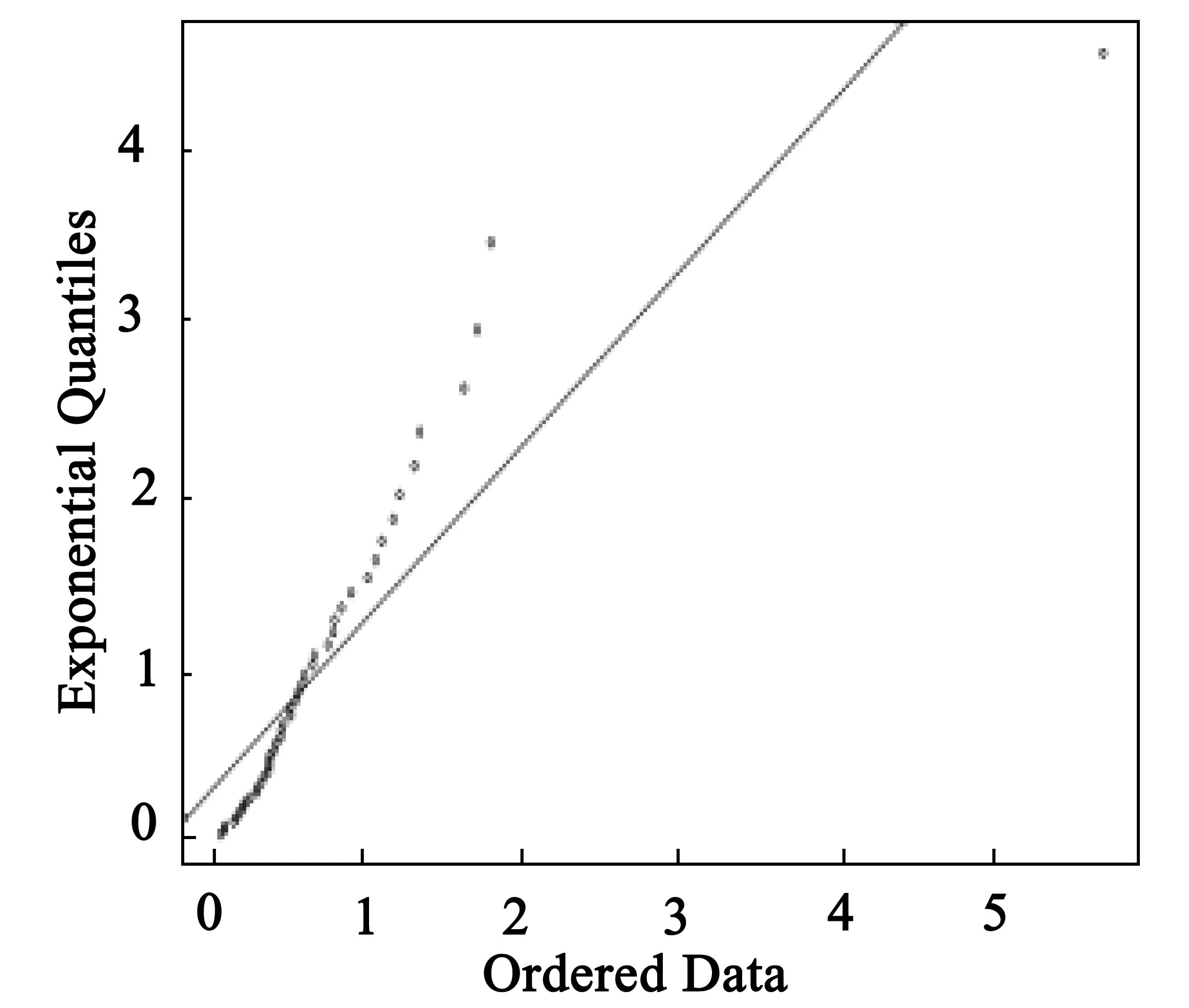

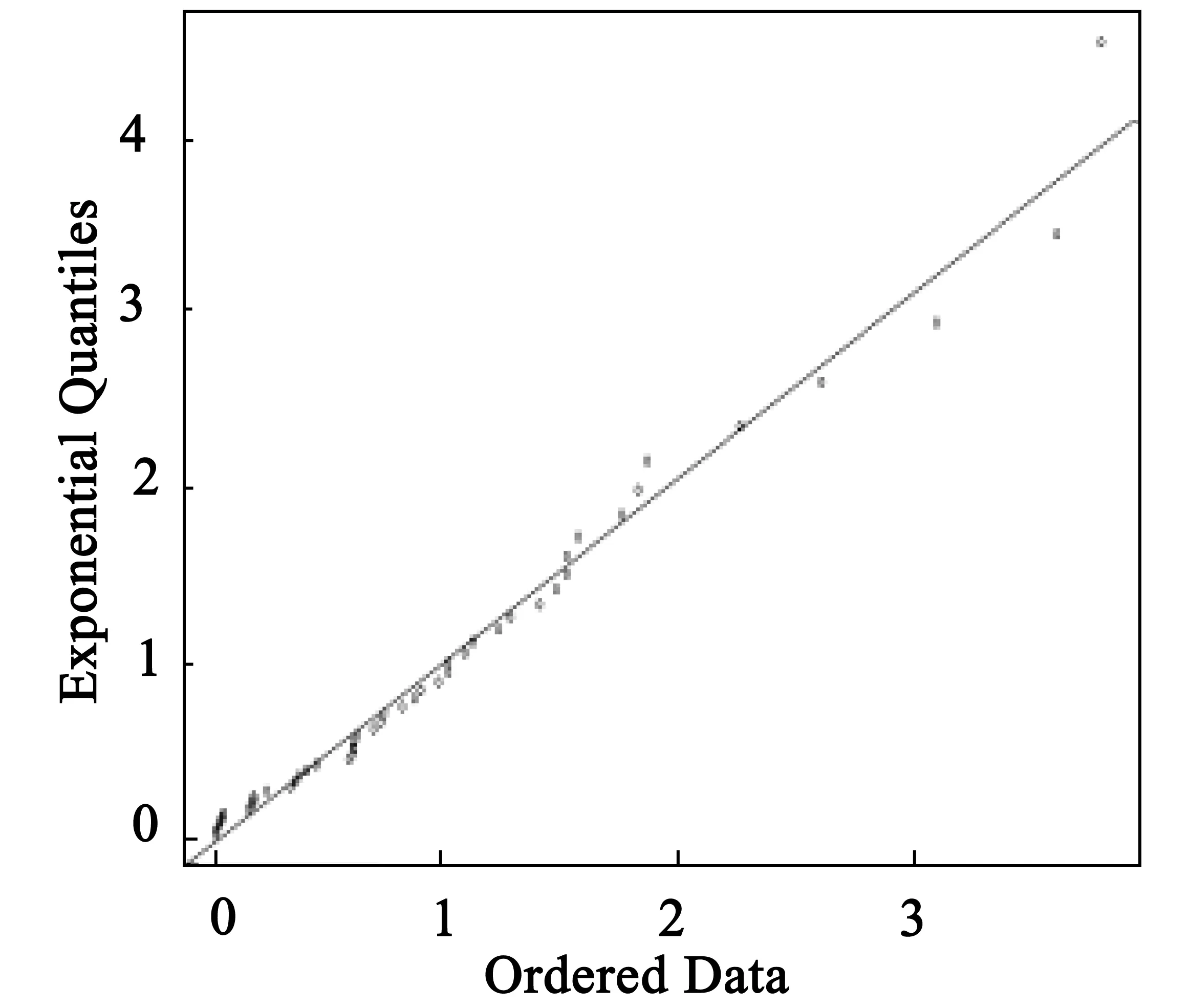
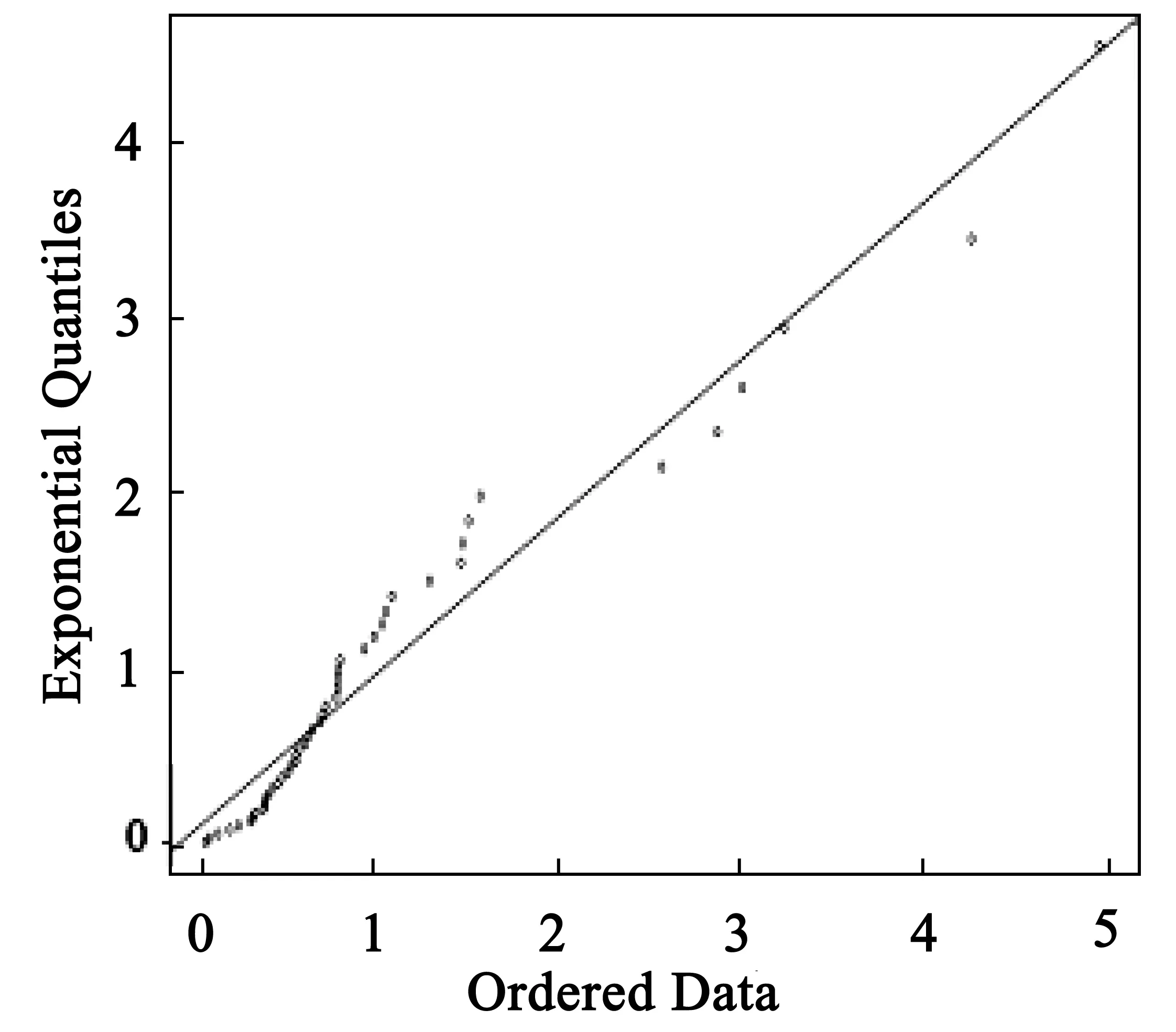
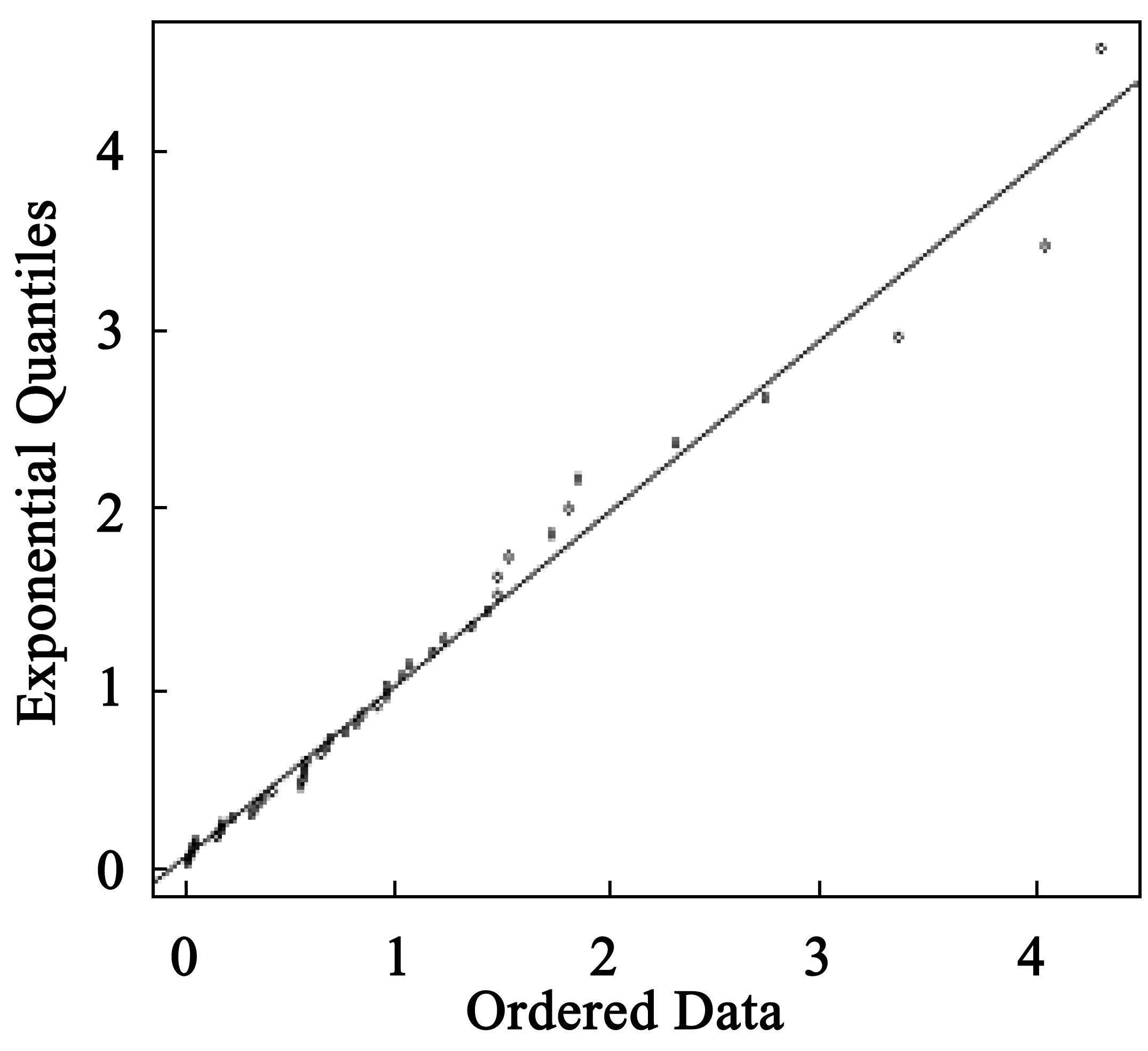
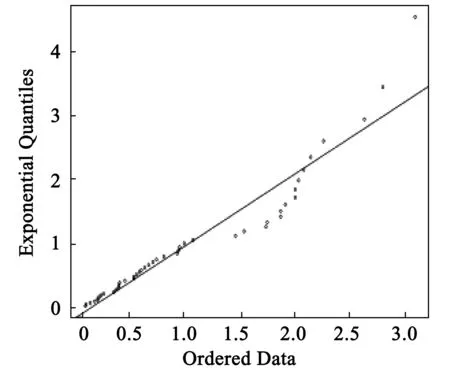
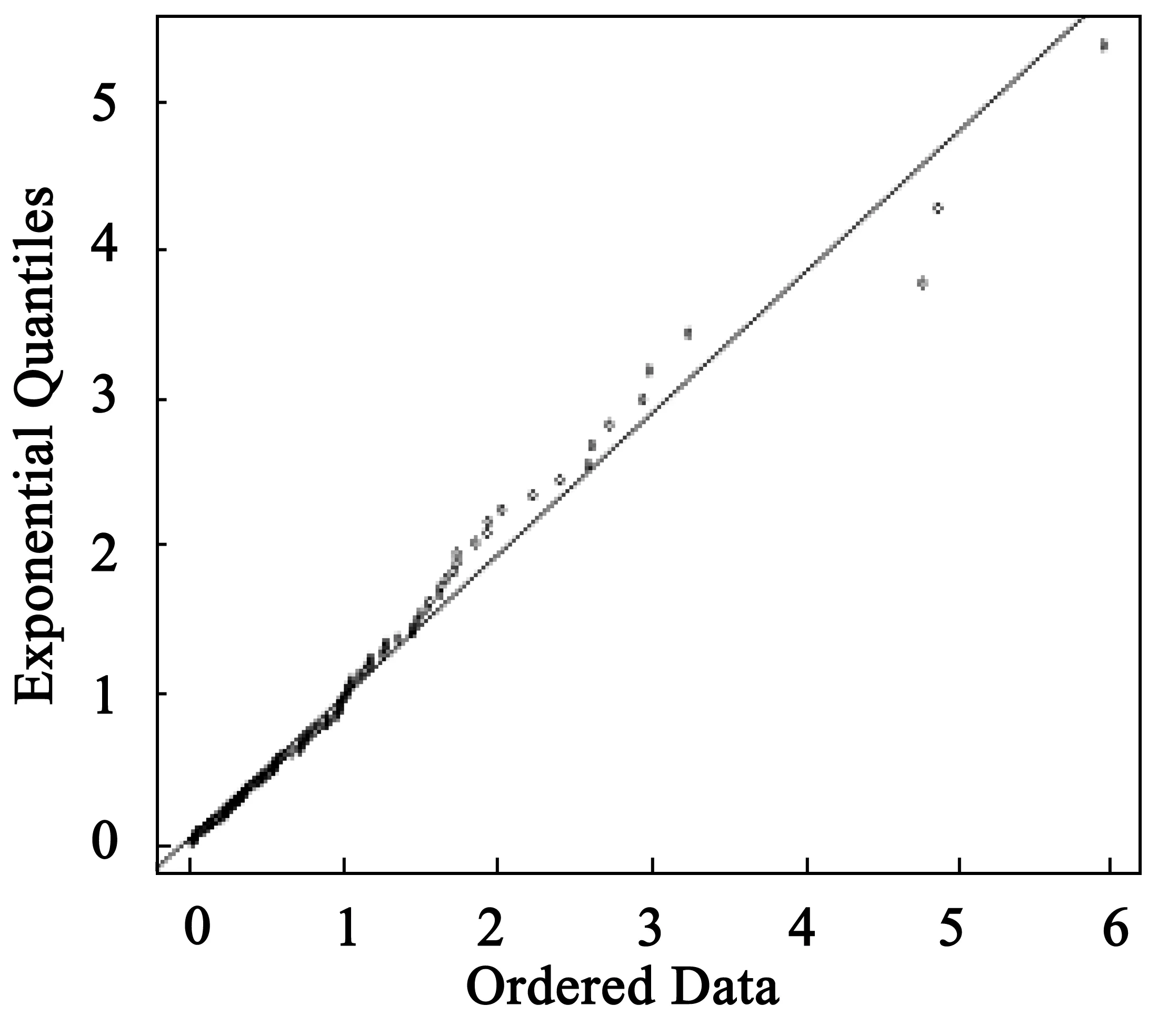
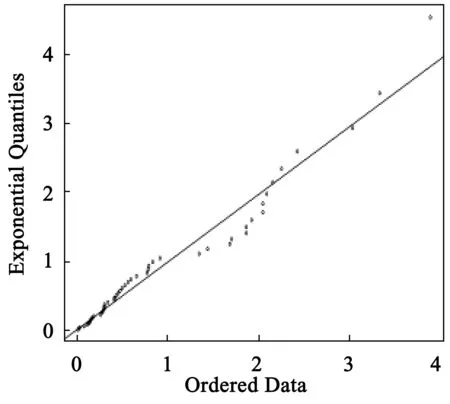
4 结语
