基于改进FCM的锤式破碎机铸造锤头质量分析

王洪平,宋良美

(湖北工业大学 机械工程学院，湖北 武汉 430068)

锤式破碎机具有结构简单、工作可靠、生产效率高等优点，在冶金、建材、矿山、交通等领域得到了广泛应用.锤头是锤式破碎机核心部件之一，它的质量直接关系到机器工作效率和使用寿命.锤头也是易损件，消耗量大，更换频繁，是主要的生产成本.锤式破碎机锤头材料常采用高铬铸铁，铸造方法一般为重力铸造和压力铸造.由于锤头结构相对比较简单，铸造工艺也不复杂，因此，生产的厂家较多，产品质量参差不齐.分析锤式破碎机锤头的质量，对指导用户购买质量优良的产品，促进生产商提高产品质量，提高设备的生产效率，延长零件的使用寿命，降低生产成本等具有重要的意义.模糊聚类算法(fuzzy clustering means，FCM)是将聚类理论与模糊理论相融合而形成的一种聚类算法.该算法通过考查样本间的相互关系，分析其隶属度，对类与类之间有交叉的数据集进行聚类[1-2].它不仅能够对样本进行分类，而且能够更加直观地分析分类结果背后的详细信息，具有良好的收敛性，是一种有效的柔性划分，广泛应用于各种领域[3-6].本文采用改进的FCM分析锤式破碎机锤头，使其质量分析进一步细化，以满足实际需要.

1 确定评价指标

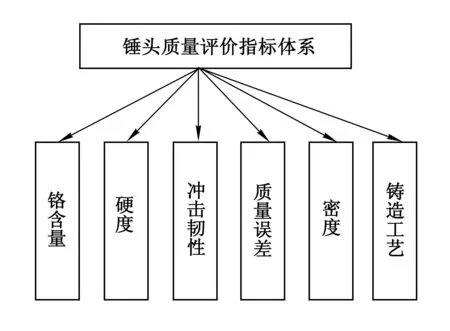
图1 高铬铸铁锤头质量评价指标体系

锤式破碎机锤头总体要求是要有稳定的工作性能和一定的使用寿命.锤头是破碎物料的主要零件，因此，耐磨和抗冲击是锤头质量的主要体现.高铬铸铁的耐磨性主要与铬的含量有关，在一定范围内，铬含量越高，耐磨性越好；密度和硬度也与锤头的耐磨性和抗冲击性有关，密度越大，硬度越高，耐磨性和抗冲击越好.另外，锤式破碎机的锤头是成组对称地布置在转轴上的，锤头质量的误差会影响到轴运转的平衡性，不平衡容易产生机器振动，对设备造成损伤.铸造工艺的好坏直接影响锤头的抗冲击、抗疲劳等性能.铸造工艺质量主要考察锤头表面是否有气孔、夹砂、砂眼、缩松、缩孔、肉瘤等铸造缺陷.本研究主要选取铬含量(B1)、硬度(B2)、冲击韧性(B3)、质量误差(B4)、密度(B5)、铸造工艺质量(B6)6个指标作为衡量高铬铸铁锤头综合质量的评价指标.高铬铸铁锤头质量评价指标体系见图1.

2 FCM算法原理和步骤

2.1 FCM算法原理

FCM的基本原理是对构建的目标函数逐步迭代、不断优化，提升数据聚类最有效性.其每一步的迭代都沿着目标函数减小的方向进行，使得被划分到同一类的对象之间相似度最大，而不同类之间的相似度最小[7-8].传统的FCM算法没有考虑指标的重要程度对分类结果的影响，进而影响分类效果的客观性和准确性.本文引进指标的权重加以改进，充分考虑了指标的重要性对分类影响.具体方法如下：

设有n个评价对象S={s1，s2，…，sn}，每个评价对象有m个属性B={B1，B2，…，Bm}，n个评价对象m个属性的评价值为X={xij}(i=1，2， …，n；j=1，2， …，m)，其中xij为第i个评价对象第j个评价指标的评价值.若将n个评价对象分成c个不同的类别，设这c个类别的中心为C={c1，c2，…，cc}，设评价对象sj与类别中心ci的距离[9-10]为：

(1)

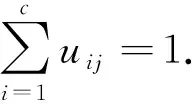
模糊c均值聚类的准侧就是使目标函数J(U，C)值到最小，即

(2)

式中，ρ为模糊因子，一般取ρ=2.0.

模糊c均值聚类的具体步骤如下：

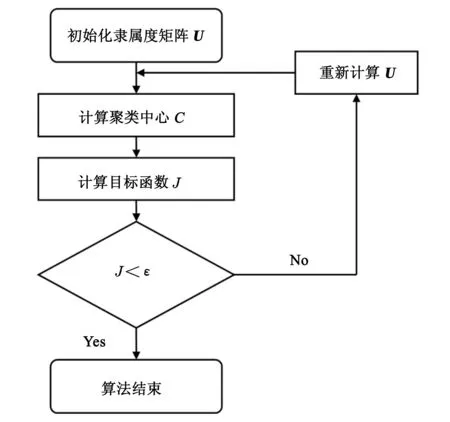
图1 FCM算法流程图

1) 给定聚类类别数目c、模糊因子值ρ，设定迭代终止阈值ε、最大迭代次数T.

2) 更新隶属度函数

(3)

3) 更新聚类中心

(4)

4) 判断是否满足终止条件.若‖J(t+1)-J(t)‖<ε，或达到最大迭代次数T，则停止运行，输出结果，否则，令t=t+1，返回步骤3).

FCM算法流程如图1所示.

2.2 数据规范化

由于每个指标的量纲和数量级不同，为了便于决策，需要对原始数据进行规范化处理.属性指标一般分为效益型(越大越好)和成本型 (越小越好)两类.不同类型的指标，规范化方法不同.

对于效益型指标，规范化采用

(5)

对于成本型指标，规范化采用

(6)

式中：xij为原始数据序列，yij为规范化数据序列.

2.3 确定指标权重

不同的评价指标对目标的贡献不同，应以权重的形式体现.传统的1～9标度法确定权重只能取整，属性的重要性最少为1个数值的差距，导致权重数值差距较大，有时与事实不吻合.本文采用一种改进的1～9标度法以弥补其不足.

首先对各指标的重要程度进行评分，分数1～10，可以为小数，不同的指标分数可以相同.然后对指标的得分进行两两比较，并通过其差值确定判断矩阵V=(vij)n×n.若评价指标Bi和Bj得分分别为ai和aj，则判断矩阵元素vij的值为

(7)

显然，vii=1，vji=1/vij.

为了保证最终指标权重的精确性，1～9 标度法通常需要进行一致性检验，其过程复杂繁琐.本文利用最优传递矩阵进行改进，使其自然满足一致性要求，无需进行一致性检验.具体步骤如下：

1) 计算V的拟优矩阵D=(dij)n×n

dij=10eij，

(8)

(9)

2) 计算B的最大特征值所对应的特征向量pi

(10)

3) 计算指标的权重wi

(11)

式中wi为指标Bi的权重.

2.4 确定加权规范化数据

加权规范化数据为评价对象各指标规范数据与其对应的权重之积，即

zij=yij·wi，

(12)

式中：wi为指标Bi的权重，yij为第j个评价对象第i个评价指标的规范化数据.

2.5 聚类

以加权规范化数据为基础，按FCM算法聚类，得到各样本的类别归属.

3 实例分析

3.1 锤头质量测试

以PC-600×400锤式破碎机锤头为研究对象.锤头材料为Cr26，质量5 kg.选择15种不同厂家生产的同一牌号的锤头进行研究.锤头质量测试参照国家有关标准，铸造工艺质量采用专家评分(满分为100分)判断，每个样本测试3次，取其平均值.测试结果见表1.

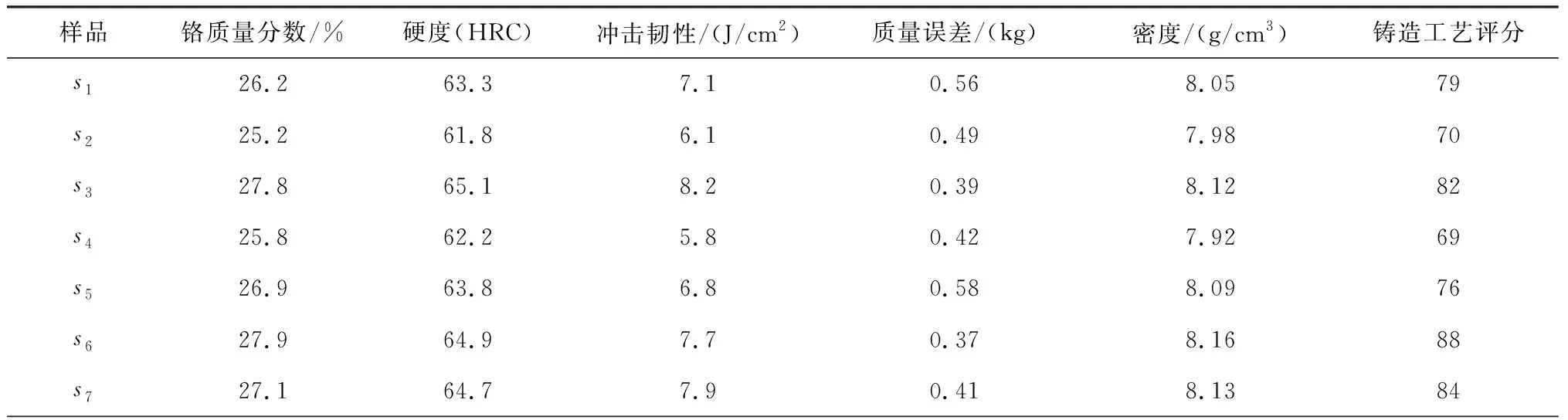
表1 锤头质量指标原始数据

续表

3.2 数据规范化

高铬铸铁锤头6个评价指标中，质量误差属于成本型指标，其余5个均为效益型指标，分别按式(5)～(6)进行规范化处理，结果见表2.

表2 数据规范化结果

3.3 确定权重

根据相关标准和实际经验，给出高铬铸铁锤头6个评价指标的重要性评分，它们分别为：s1=10.00，s2=9.75，s3=9.50，s4=9.25，s5=9.00，s6=8.75，s7=8.25.

按照式(7)构造判断矩阵V:

按照式(8)～(9)求出拟优矩阵D：

按照式(10)～(11)求得评价指标的权向量和权重分别为：

P=(1.414 1，1.310 5，1.081 6，0.909 3，0.690 0，0.641 0)，

W=(0.233 8，0.216 7，0.178 9，0.150 4，0.114 1，0.106 1).

3.4 确定加权规范化数据

按式(12)计算加权规范化数据，结果见表3.

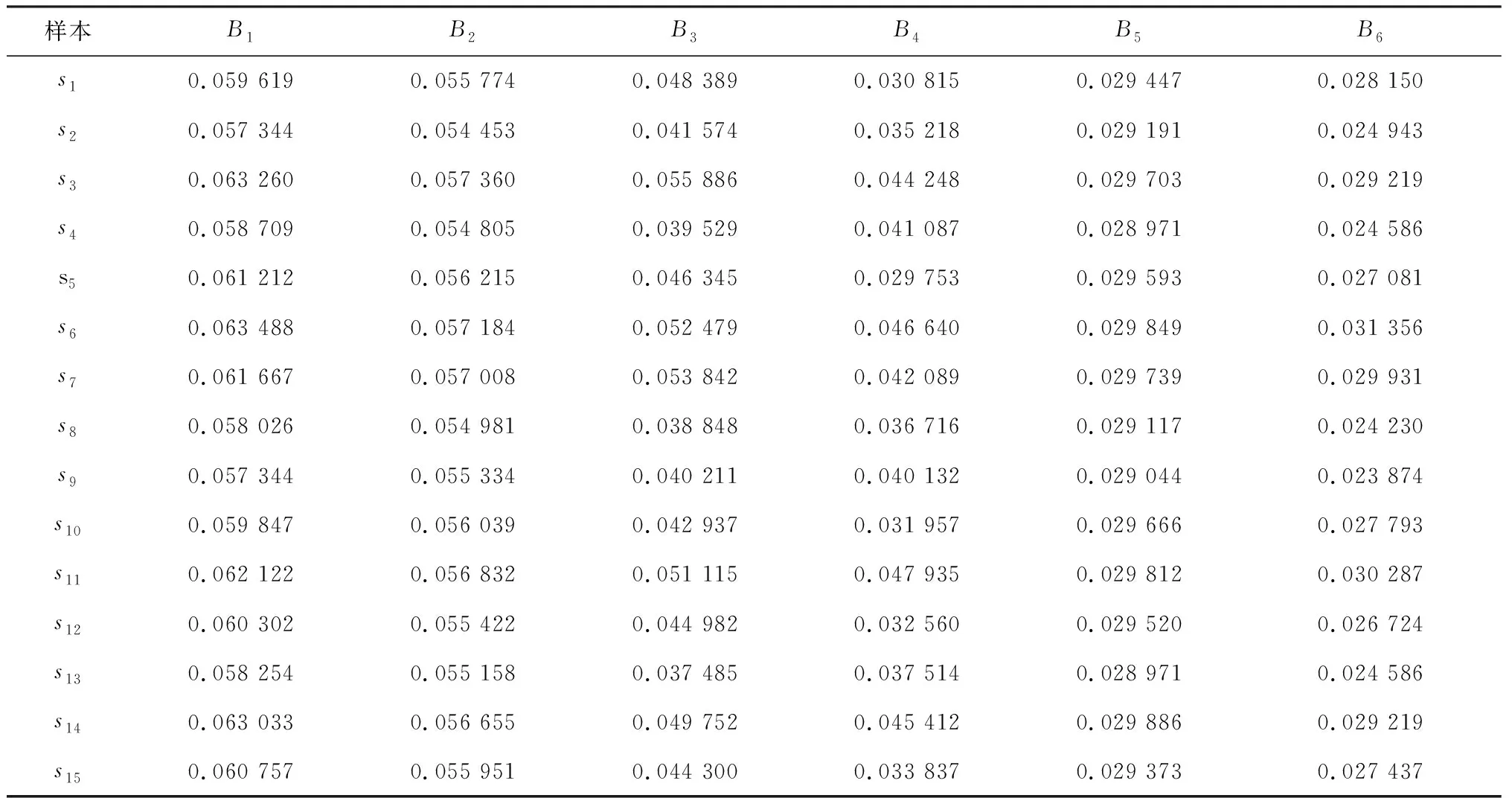
表3 加权规范化数据

3.5 聚类

按2.1方法进行聚类，取阈值ε=0.000 1，最大迭代次数T=30，聚类数目c=3.据此，得到各样本属于3个类别的隶属度(表4)，继而得到分类的结果(表5).聚类直观图如图2所示，目标函数随迭代次数变化如图3所示.从图3可知，算法收敛很快，在迭代7次左右就计算完毕.通过分析隶属度函数，不仅可以知道样本归属的类别，而且还可以知道样本归属类别的程度.如样本s1，归属3个类别的隶属度分别为：0.888 570，0.067 904，0.043 526，按照隶属度最大原则，应划归C1类，且程度很高，隶属度为0.888 570，属于C2、C3的隶属度很小，隶属度仅为0.067 904和0.043 526.

表4 样本对应类别的隶属度

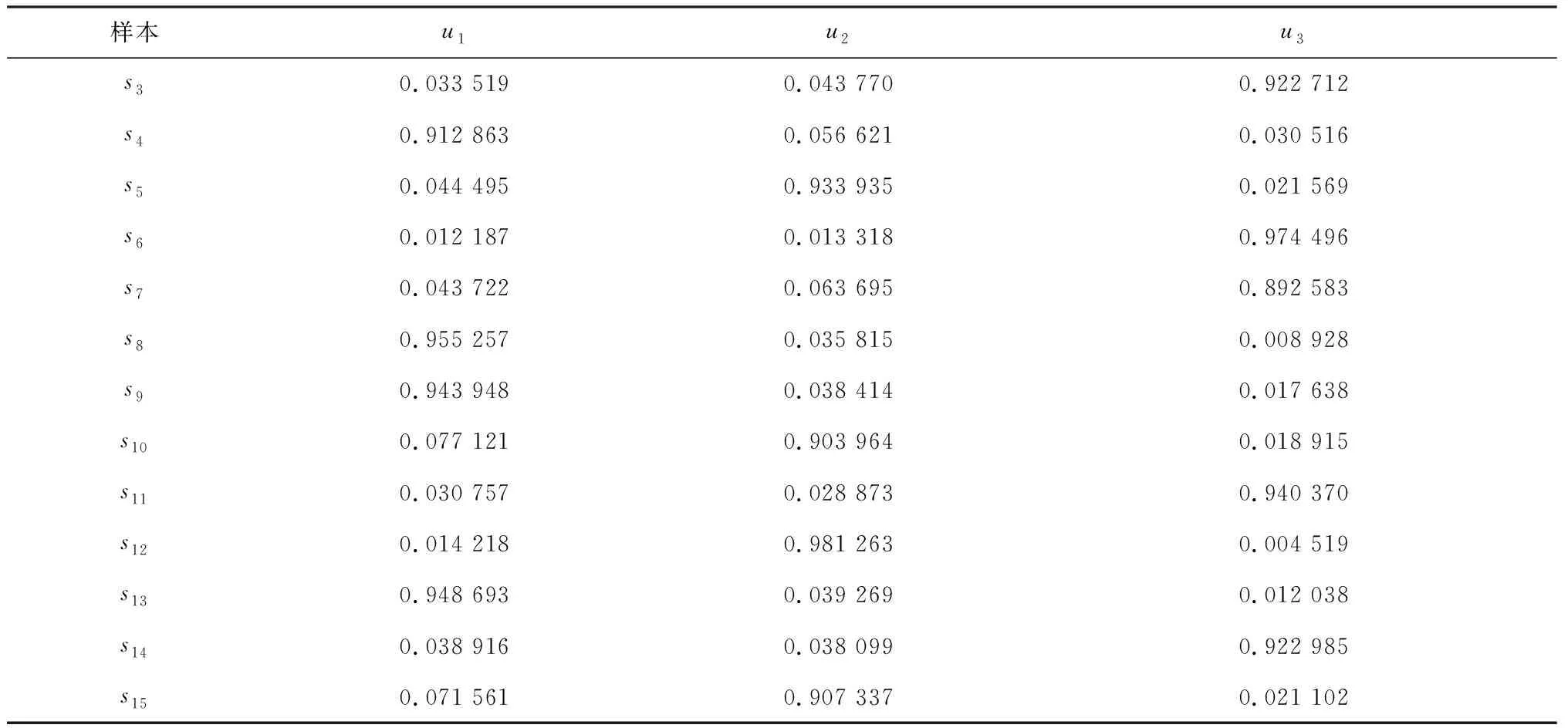
续表

表5 分类结果

图2 聚类结果直观图

图3 目标函数随迭代次数变化图

3.6 判断类别的优劣

从分类情况看，s2是第1类的代表元素，s1是第2类的代表元素，s3是第3类的代表元素，从表1的原始数据看，s3优于s1及s2，故3类样品的性能优劣排序为：C3>C1>C2，即第3类的高铬铸铁锤头质量最优，第2类的高铬铸铁锤头质量最差.

4 结语

锤式破碎机的锤头是机器的关键零部件，其铸造质量与设备的使用和维护成本密切相关，选择优良的锤头，对保证机器正常运转、提高工作效率、节约生产成本等至关重要.模糊c-均值聚类算法是聚类算法中的一个重要分支，它在分类过程中引入隶属度函数，使分类更加直观可信.FCM分类的核心是使同一类别的对象之间相似度最大，不同类别对象之间相似度最小，这种相似度通过隶属度函数来实现.聚类结果依据每个数据点对聚类中心的隶属程度决定，不仅能知道样本所属类别，而且能更进一步了解所属类别的程度，分类结果更为客观可靠.本文运用改进的模糊c-均值聚类算法对锤式破碎机高铬铸铁锤头的综合质量进行了聚类分析，进一步细化了其质量评判，对用户正确选择产品，促进生产商提高工艺水平，生产出高质量的产品来满足市场需要具有积极的作用.