近似支持向量机的AVO类型判别
2018-09-20李文秀文晓涛李雷豪刘松鸣杨吉鑫
李文秀 文晓涛 李 天 李雷豪 刘松鸣 杨吉鑫
(①成都理工大学地球物理学院,四川成都 610059; ②成都理工大学油气藏地质及开发工程国家重点实验室,四川成都 610059; ③云南建投第一勘察设计有限公司,云南昆明 650031)
1 引言
AVO技术研究并利用地震波振幅与炮检距的关系进行油气预测,对于储层含油气分析有着十分重要的意义。因含气砂岩压实程度差异,与上覆盖层形成不同的物性参数组合,其反射系数随入射角的变化特征也不同。目前,主要有四类含气砂岩的AVO特征曲线,前三类由Rutherford等[1]提出,Castagna等[2]补充了第Ⅳ类。其中第Ⅱ类和第Ⅲ类AVO异常是烃类检测的有效标志,通常在叠加剖面上形成“暗点”或“亮点”异常。经过20多年的发展,AVO技术得到了广泛的应用,在油气勘探中扮演了重要角色[3-6]。
目前储层AVO类型描述的主要途径是人工识别,但受人为干扰因素大、可靠性低。有学者利用神经网络和支持向量机(SVM)判别储层AVO类型[7,8],但在处理大数据量的地震资料时计算效率低、稳定性差。SVM算法由Vapnik等[9-11]在20世纪90年代提出,与神经网络算法相比,具有严格的理论和数学基础,避免了过于依赖经验,分类结果更真实可靠,在地震反演、地震属性优选与测井数据处理方面都得到了广泛应用[12-17]。SVM算法最大的缺点就是难以对大数据样本进行高效处理。为了解决这一问题, Fung等[18]在SVM的基础上提出了近似支持向量机(PSVM)算法,将传统SVM算法中的不等式约束变为等式约束,使PSVM算法在运算速度和稳定性方面优于SVM。Zhao等[19]基于地震属性应用PSVM算法识别页岩; Zhang等[20]将多种地震属性作为输入参数,运用PSVM算法划分页岩储层脆性; 刘佳乐等[21]应用PSVM算法刻画储层流体性质。
本文从四类AVO曲线中提取特征参数作为训练集,引入PSVM算法对叠前地震资料中提取出的特征参数进行判别,实现对研究区储层AVO类型的自动识别。
2 原理
2.1 支持向量机
SVM是Vapnik等[9-11]在统计学习理论的基础上提出的一种采用结构风险最小化准则的新学习方法,可以用于样本分类。
已知有一个定义在n维空间上的训练样本集{(xi,yi),i=1,2,…,m},xi=[xi,1,xi,2,…,xi,n]T∈Rn表示样本,样本中的每一个属性都与向量中的元素一一对应。yi∈R为样本输出值,若是两类分类问题,则可用yi=+1和yi=-1分别表示样本的类别标签。决策函数f(x)的形式为
f(x)=sgn[g(x)]
(1)
g(x)=ω·x+b
(2)
式中: sgn(·)为符号函数;ω=[ω1,ω2,…,ωn]T为系数向量;b为常数。基于最大间隔原则引入松弛变量ξi(i,1,2,…,n)及惩罚参数C(C>0,C越大说明惩罚越严重),得到最优化问题
满足yi(ω·xi+b)+ξi≥1
ξi≥0
(3)
计算得到最优解ω*和b*。最终根据式(1)和式(2)求得决策函数
f(x)=sgn[(ω*·x)+b*]
(4)
2.2 近似支持向量机
Fung等[18]在SVM的基础上提出了PSVM,在准确度不低于传统SVM的前提下突破了运算效率的瓶颈,适合处理信息量丰富的数据集。PSVM将传统SVM算法中的不等式约束变为了等式约束,由求解一次线性方程组问题替换了原来的凸二次规划问题。PSVM在对大数据量样本集进行学习过程中大幅度缩减了计算量,提升了训练速度,能够在不损失识别精度的前提下进行快速学习。
基于PSVM的等式约束,构建最优化问题
满足D(Aω+eb)+ξ=e
(5)
式中:矩阵Am×n表示训练集;D为m×m的对角矩阵;e为单位向量。求解式(5)同样可获得最优解ω*和b*,代入式(4)求得决策函数f(x)。计算结果f(x)=-1则该样本与标签y=-1的样本为同一类;相应地,当f(x)=+1时,该样本属于y=+1所在类。训练结果g(x)=0表示超平面是线性的,实现了目标的线性划分。将核函数引入最优化问题中可以实现从低维非线性空间映射到高维特征空间的简化,在高维特征空间中寻找最优超平面,从而实现目标的非线性划分。
2.3 基于PSVM的多类分类
近年来,在两类分类的基础上推广到基于PSVM的多类分类方法。目前基于PSVM实现多类分类主要有两种方法:一类对余类算法和成对分类算法[22,23]。对于训练集
T={(x1,y1),(x2,y2),…,(xl,yl)}
(6)
式中:xi∈Rn,yi∈{1,2,…,M}。目的就是通过寻找一个与其对应的判别函数f(x):x∈Rn→y实现目标的多类分类。
2.3.1 一类对余类算法
一类对余类算法是解决多类分类问题最早采用的方法。对于M(M≥2)类分类样本集,首先利用一类对余类方法提出某一类样本作为+1类,剩余所有样本作为-1类,构造成M个两类分类问题。利用PSVM分类,得到其中某一个判别函数,简记为f1=sgn[g1(x)],进行M次判别之后,得到判别函数集:f1,f2,…,fM。对新数据进行判别决策时,将其依次代入判别函数的gi(x)(i=1,2,…,M),gi(x)中最大值所对应上标所属的类就是当前的判别结果。
2.3.2 成对分类算法
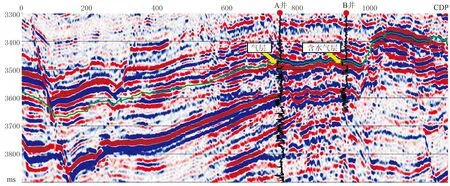
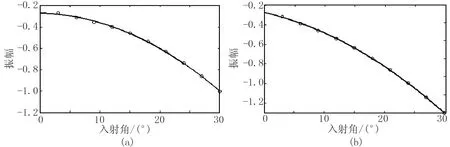
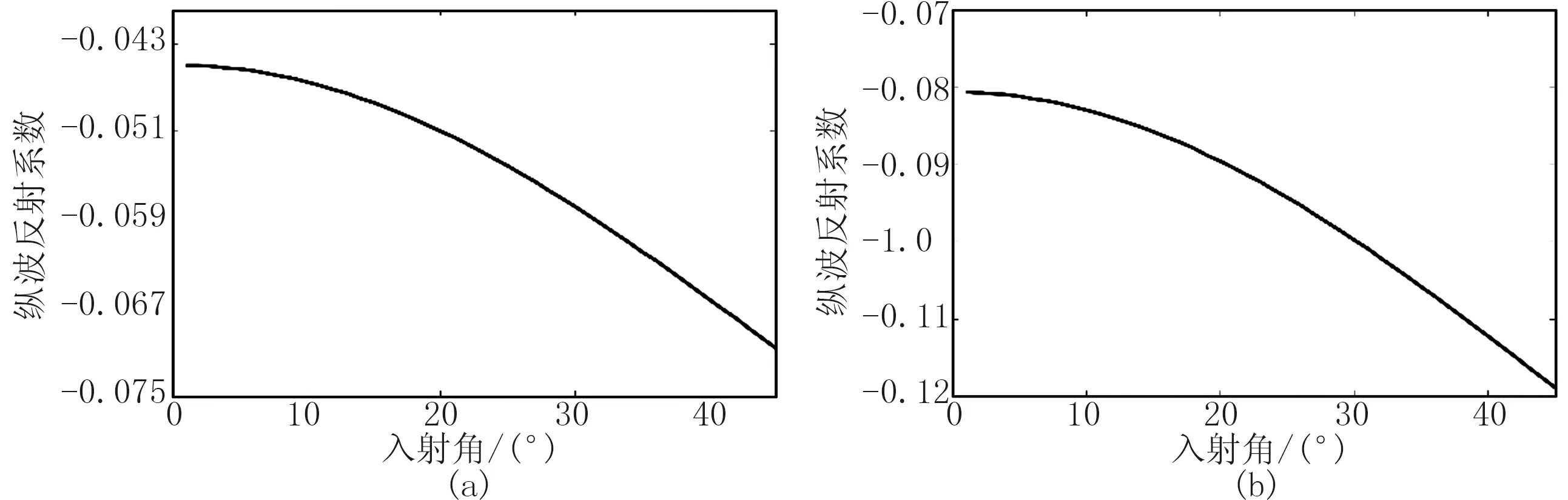
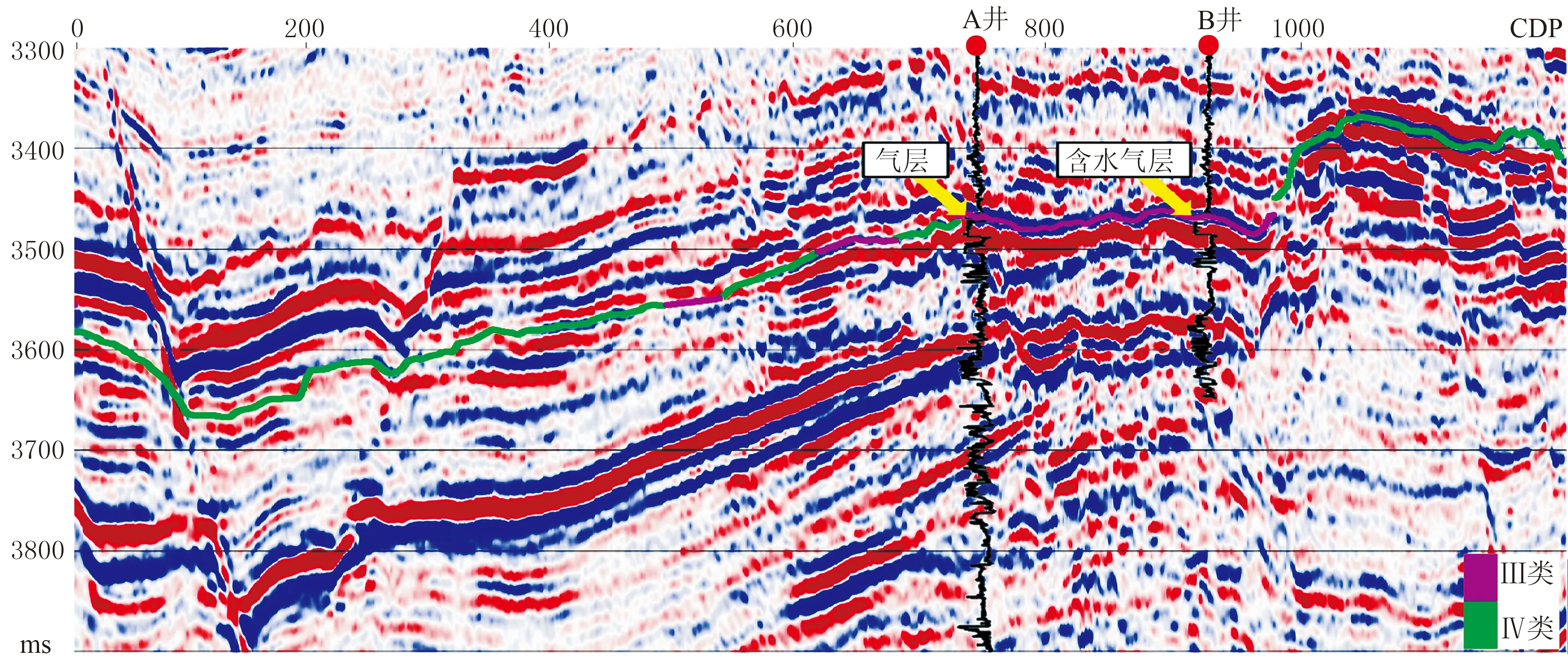
成对分类算法同样也是将多类分类问题分解为若干个两类分类问题,对于M个样本,需要构造(M-1)M/2个分类器。从训练集中分别提取出一个i类样本和一个j类样本,{(i,j)|i (7) 对于一个新的待判别样本,将其依次代入每一个判别函数,当判别结果为某一类时,就在那一类的票数上加1,最后将此样本判别为票数最多的那一类。如果出现两类票数相等的情况,则将样本判别为类别序号较小的那一类。 从反射系数随入射角的变化特征入手,将四类AVO曲线的形态特征参数进行量化,形成训练集。利用PSVM对训练集进行训练获得判别式,然后利用判别式就可以划分研究区的AVO类型。 利用研究区的测井资料建立弹性参数模型(表1),通过Shuey近似公式求取反射系数曲线(图1)。因为计算出的反射系数曲线是离散的,很难从中提取出形态参数,所以对离散数据进行多项式拟合。图1中连续的曲线就是用多项式拟合结果,用拟合函数表达式就可以提取反射系数曲线的形态特征参数。 表1 训练模型参数 图1 四类AVO反射系数随入射角的变化曲线 从图1中可以看出,四类AVO反射系数曲线的形态变化是不同的,Ⅰ类、Ⅲ类、Ⅳ类AVO因为储层与盖层的波阻抗差异大,所以在法线入射时的反射系数绝对值比较大; Ⅱ类AVO的储层与盖层的波阻抗差异较小,所以法线入射时的反射系数绝对值趋近于0。Ⅰ类AVO曲线随入射角增大反射系数减小,其值也逐渐由正转负,会出现极性反转现象; Ⅳ类AVO的反射系数绝对值随入射角增大而变小。四类含气砂岩的反射系数随入射角的变化各有不同,就可以从上一步中得到拟合函数表达式提取形态特征参数。形态特征参数主要包括曲线的单调性、凹凸性、极值点的个数和所在的位置、拐点的个数和所在的位置。将这些信息提取出来就形成了训练集和样本集(表2)。 表2 训练集样本(部分) 形成的训练集可记为T={(x1,y1),(x2,y2),…,(xl,yl)},其中l为样本个数,提取的特征属性有13个,即xi∈R13。标签根据实际情况制定,若是多个类别(设有M个类)的模型参与训练和判别,则标签按照多类分类的方式依次确定为1,2,…,M。待判别的AVO数据也需经多项式拟合后提取属性形成待判别样本。最后利用PSVM训练后得到的判别式对待判别样本进行分类。 通过以上步骤建立了一套基于PSVM的AVO类型判别的流程(图2),因为在实际地震数据应用时,是从地震波振幅随角度的变化曲线中提取形态参数,所以可以通过实际工区的井中子波和四类AVO的反射系数褶积合成地震记录来制作训练集。 图2 基于PSVM的AVO类型判别流程 利用上述基于PSVM的AVO类型判别流程,对南海N气田进行AVO类型识别。研究区目的层为砂岩,储层上方为泥岩,为三角洲沉积,储层物性较好。通过合成记录(图3)可标定砂岩顶、底位置(图中绿色、橙色线所示)。从测井曲线可以看出含气层段(图中灰色阴影段)的波阻抗、伽马值和泊松比呈现低异常值。图4是过A井和B井的南北向连井地震剖面,图中的黄色箭头分别指示了A井和B井的储层位置,测井曲线为伽马曲线。A井在砂岩储层钻遇工业气流,测井解释显示A井气层段的细砂岩孔隙度为23.0%,渗透率为23.3mD,含水饱和度为29.0%;B井钻遇含气水层,该段的孔隙度为19.3%,渗透率为62.5mD,含水饱和度为62.5%。 图3 B井的井震标定结果 图4 南海N区的连井地震剖面 通过以上分析,可知研究区储层的孔隙发育较好,渗透率高,压实程度不高,波阻抗较盖层小。原始数据的井旁道集振幅随入射角变化较为复杂(图5),所以通过拟合将原始数据规则化,并求取拟合的公式以便样本集的提取。从拟合后的井旁道目的层地震数据的振幅随入射角变化曲线中可以看出,A井(图6a)和B井(图6b)在法线入射时的振幅较高,振幅的绝对值随入射角增大而增大,说明研究区储层属于Ⅲ类AVO。利用两口井的测井资料建模,数值模拟该区的AVO响应,从数值模拟的结果看出,A井(图7a)和B井(图7b)的AVO响应特征与图6相似,都属于Ⅲ类AVO的特征。研究区含气储层的AVO响应特征以第Ⅲ类为主。 通过叠前数据形成样本集以后,利用PSVM对该地区的叠前地震资料进行AVO类型识别,结果如图8所示,其中亮紫色表示Ⅲ类AVO,可以看出井旁的AVO类型属于第Ⅲ类,与上文数值模拟的结果吻合,说明了利用PSVM判别AVO类型是可靠的。 图5 井旁振幅随入射角的变化曲线 图6 拟合后的井旁道振幅随入射角的变化曲线 图7 基于测井数据建模的AVO响应数值模拟 图8 AVO类型识别结果 本文从AVO曲线的形态特征入手,通过近似支持向量机对不同类型的AVO形态特征参数进行分类,划分出研究区内的第Ⅲ类含气砂岩的分布。从实际应用结果可以看出判别结果较为准确,说明本文提出的基于近似支持向量机的含气砂岩AVO类型判别方法有较高的应用价值。3 基于近似支持向量机的AVO判别
3.1 训练集的准备
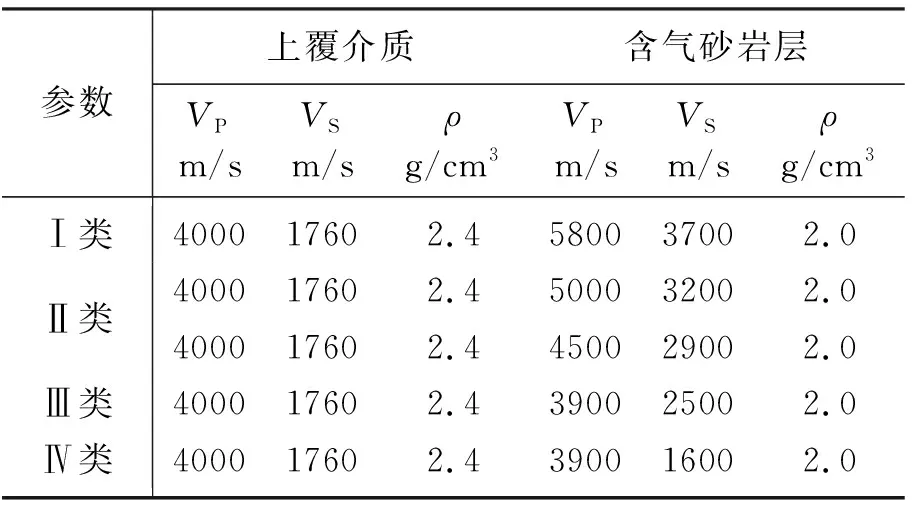
3.2 特征值的提取
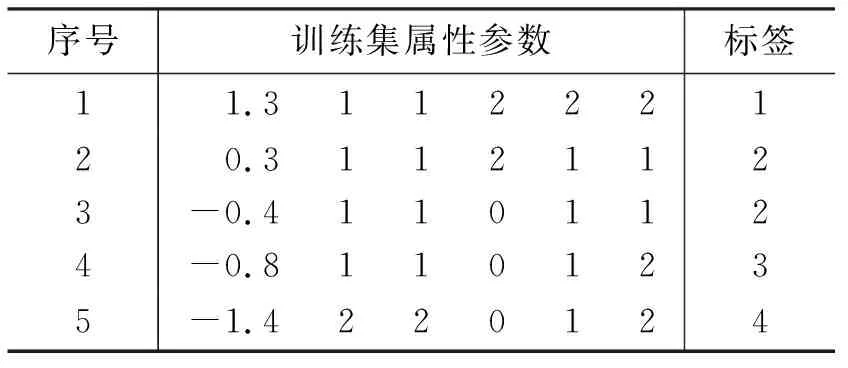
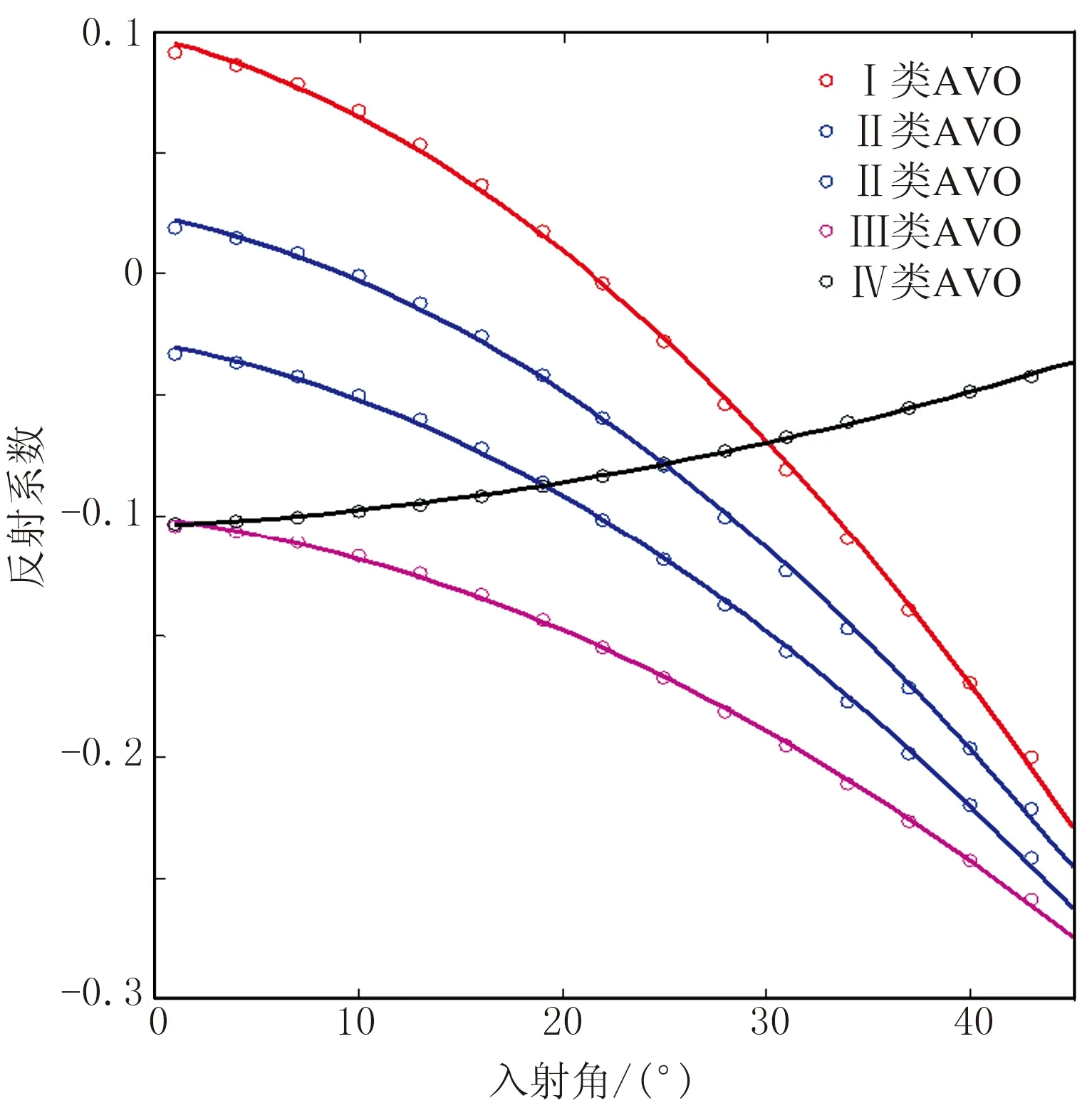
3.3 PSVM判别
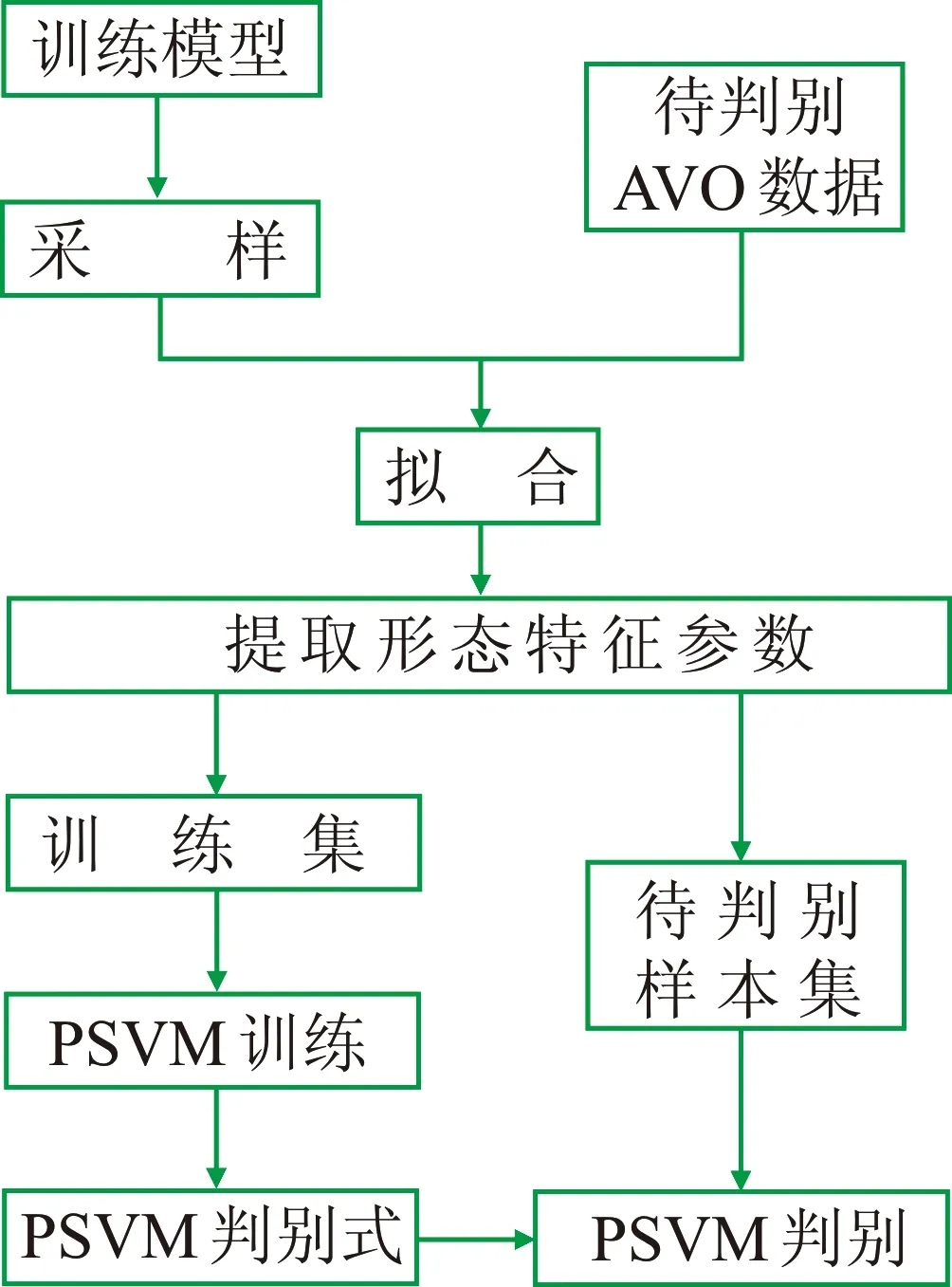
4 应用实例


5 结束语
