等效介质理论激电模型频率相关系数的影响因素

昌彦君 托乎尼牙孜·吐尼牙孜* 王汉雨

(①中国地质大学(武汉)地球物理与空间信息学院，湖北武汉 430074; ②武汉捷探科技有限公司，湖北武汉 430074)

1 引言

频谱激电法(SIP)和时频电磁法(TFEM)是石油天然气勘探中非常有效的非地震勘探方法。油气藏本身具有与围岩明显不同的物理化学性质，大量岩心测试和测井的电阻率与极化率统计数据，以及多个含油气盆地的勘探成果表明：油(气)在生成、运移、聚集和逸散的空间上都存在电性—电极化性异常，为应用SIP或TFEM进行油气藏勘探或油气检测提供了物性前提。这两种方法均利用了电磁效应和激电效应，都具有反演参数多的特点，为综合解释、构建油气识别模式提供了丰富的参数信息，其中的频率相关系数在油气中心及边界检测等方面取得了较好的勘探效果[1-7]。

许传建等[1]在已知工业油井上进行复电阻率法(也称CR)探测，得到的频率相关系数异常范围为0.6～0.9；苏朱刘等[2]用SIP法对已知油田周边地带的试验区进行探测圈定了IP异常区，频率相关系数为相对低值区(<0.2)，这比典型值(0.25)略低；万明浩等[4]用SIP法对江苏J油田进行探测后得到的SIP视谱参数组合特征表现为：视充电率(M)不高(7%)，视时间常数(τ)不大(0.61s)，视频率相关系数(c)较高(0.75)；崔先文等[5]对大港油田某井段直接探测，发现本区油藏圈闭上的频谱激电参数异常模式表现为高视充电率、低视时间常数、低视频率相关系数的组合特征，在油气运移通道区M≥15%、τ>0.5s、c≥0.65；而在油气聚集区和逸散区，M从12.5%逐层向浅部减弱至5%(含油圈闭中油气向上逸渗散失所致)；时间常数和频率相关系数的低值区(τ<0.5s，c<0.65)主要分布在油气逸散区，即低值区的下部或其底部的低值异常区反映了受油气渗漏长期作用而蚀变的围岩特征，指明了上述含油气圈闭体的位置应在其低值区的下部或其底部。赵一丹等[6]用TFEM法对T盆地的含油气有利区进行探测，发现在已知构造油气藏和其两侧均有高频率相关系数异常，其值达到约0.75，并综合其他激电参数认为已知油气藏两侧可能存在受储层控制的岩性油气藏。孙志华等[7]对尼日尔A区块开展TFEM勘探，通过提取多种反映油气异常的激电参数，发现地层介质中油气藏极化效应非常明显，其油气相关的激电参数均具有较强异常，即表现为高极化率、高频率相关系数、较小时间常数，对油井和油气显示井的分析发现一级有利区的频率相关系数异常值范围为0.75～1.00，二级有利区为0.72～0.75，三级有利区的为0.70～0.72,即各级含油气有利区的频率相关系数均大于0.70。

由此可见，频率相关系数在SIP和TFEM法的多参数综合解释、以及组合参数对油气异常的定性描述中都得到了很好的应用，虽其数值的相对大小因地区而异，但其异常在油气藏有利区的预测中起到了非常好的指示作用。与反映地下介质的导电性和电化学活动性相对强弱的电阻率异常和极化率异常相比，频率相关系数的异常信息能从不同的侧面反映地下地质体的含油气特征和电性结构，可作为油气异常检测的辅助参数。但是，其相对大小的物理指示意义并不十分确切。目前，关于频率相关系数c的一般认识主要有：导电矿物颗粒度不均匀的岩矿石频率相关系数c较小，而粒度较均匀的岩石具有较大c[8]。实际露头测定的岩石的频率相关系数值范围为0.1～0.6，常见值为0.25； 实验室测得的电子导电岩心的频率相关系数和人工制造的电子导电颗粒尺寸均匀的大多数岩石的频率相关系数都大致等于0.5[9-12]； 频率相关系数与矿化类型关系不密切[13,14]。罗延钟等[14]在理论上研究了岩矿石面极化频率相关系数c(s)与体极化频率相关系数c的关系，得出结论c≤c(s)，此式在岩矿石内导电矿物颗粒度均匀时取等号，并指出： 岩矿石内含有若干种不同大小的极化颗粒时，因为不同大小的颗粒具有不同的时间常数，这样即使每一种颗粒的频率相关系数相同，由于时间常数不同而使整个岩矿石的复电阻率频谱变宽，致使体极化岩矿石的c值变小。

实际上，频率相关系数是通过反演实测的谱激电数据获得的[15-18]。单一的Cole-Cole模型简单、参数少，特别适合描述电子极化机理的复电阻率特征，在金属矿勘探中广泛应用，效果明显[19,20]。当岩石内含有多个不同极化颗粒时，其复电阻率虚分量或相位频谱曲线可能出现多个峰值，此时用多个Cole-Cole模型的加减或乘除组合，会使模型参数数量增加，且这些参数定义并不确切，很难验证它们分别对应着何种极化机制。GEMTIP模型是基于经典的等效介质理论(EMT)提出来的一种严格的数学物理模型[21-23]，是对Cole-Cole模型的扩展，对于多相复合电导介质它具有严格的数学表达式，同时包括了面极化和体极化效应，适合描述与电子极化机理相关的电极极化效应和与离子导电有关的薄膜极化效应[24,25]，并且模型参数表征明确，其参数与岩石中极化颗粒的大小、形状、极化特性等物理属性相关联，这为区分多相复合岩矿石提供了一种定量分析方法。本文基于GEMTIP模型，在理论上研究岩矿石内含有多种极化颗粒时的复电阻率频谱曲线的频率特性，从而分析极化颗粒的尺寸、形状和种类变化对频率相关系数c的影响[26]。

2 GEMTIP模型

2.1 球形颗粒GEMTIP模型

根据GEMTIP模型的基本思想，岩石基质中所含矿物颗粒可视为不同半径的球形颗粒，在准静态条件下，岩石宏观尺度上的等效复电阻率ρe可表示为[22]

(1)

式中

(2)

式中：ρ0为基质电阻率；ρp是第p种颗粒的电阻率；Fp是体积分数；ω=2πf是圆频率，f是频率；τ是时间常数；a是颗粒平均半径；α是面极化系数；N表示岩矿石中含有的颗粒种类数。

基于式(1)对两相球形颗粒GEMTIP模型进行变换处理可以得到类似于Cole-Cole模型的等效复电阻率表达式

(3)

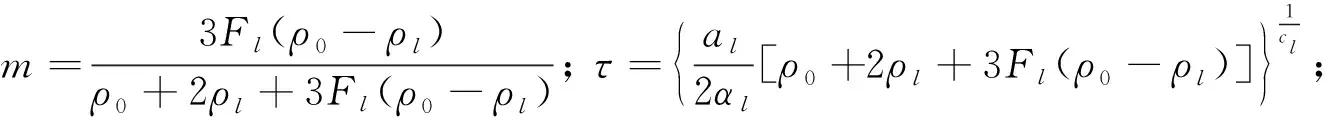
由上式可见：Cole-Cole模型是两相球形颗粒GEMTIP模型的一种特殊形式，且Cole-Cole 模型与GEMTIP模型中频率相关系数c是一样的。

实际上，Cole-Cole模型是实验观测模型，模型参数有充电率m，时间常数τ和频率相关系数c。已证实大多数岩石的激电谱可以用Cole-Cole参数定量描述，但是其模型参数定义不明确，只能通过实验观测反演获取参数后才能与已知的岩石物理属性建立定性的函数关系，即Cole-Cole模型只能在岩石尺度上描述岩石的激电效应，而GEMTIP模型的参数定义明确，如式(2)所示，其值直接与岩石内颗粒的大小、极化特性等相关，这为研究模型参数的影响因素在矿物颗粒尺度上提供了一种定量分析方法。

2.2 椭球形颗粒GEMTIP模型

当岩石中的椭球形颗粒取向完全无序、且颗粒电阻率相对基质电阻率很低时,其等效复电阻率ρe可表示为[25]

(4)

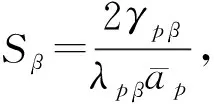
式(1)和式(4)中，当岩矿石只由基质和一种等大小、同形状的颗粒组成时，N=1，此时称为两相GEMTIP模型；岩石由基质和大小、形状或种类不完全相同的多个不同极化颗粒组成时，N≥2，称为多相GEMTIP模型。

3 频率相关系数的研究

3.1 频率相关系数的意义

频率相关系数c在频谱激电法中主要表征复电阻率随频率变化的快慢，表现为频谱曲线的陡缓程度。c越大，频谱曲线越陡，且频谱的变化范围越窄[24]。图1给出了当式(1)中N=1时的两相球形颗粒GEMTIP模型的其他参数固定时，不同频率相关系数c的复电阻率虚分量imag(ρ)的频谱曲线。

由图1可知，随着c的减小，频谱曲线的变化范围越来越宽，当c=0.1时，曲线几乎为直线。此外，图中虚分量频谱曲线是轴对称的，并且只有一个峰值，这是因为两相GEMTIP模型中假定岩石只由基质和一种等大小的颗粒组成，当基质不极化时，岩石内只有一种等大小的极化颗粒，相当于岩石内只有一个体极化体单元，因此频谱曲线反映的就是单个极化体。但实际的岩石中颗粒大小往往参差不齐，形状各异，有的还含有多个不同极化特性的矿物颗粒，此时其复电阻率频谱曲线不再像图1所示一样地对称。设置几种含有多个不同极化颗粒的理论模型分析影响频率相关系数c变化的因素。

图1 两相球形颗粒GEMTIP模型复电阻率虚分量随频率相关系数的变化曲线

3.2 频率相关系数的影响因素分析

一般岩石由多个不同类型的颗粒组成，这些颗粒的大小、结构或种类可能不完全相同，可以用多相GEMTIP模型描述其复电阻率的频率特性[21-23]。本文以三相GEMTIP模型为例分析岩石中极化颗粒大小的均匀程度、形状和种类对频率相关系数c的影响。

假设岩石由基质和两种颗粒组成，其中基质不极化，颗粒可极化。基于式(1)和式(4)建立3个三相岩矿石GEMTIP模型： 模型1岩石含有不同粒度的两种球形颗粒；模型2岩石含有球形颗粒和椭球形颗粒； 模型3岩石含有不同面极化系数αp的两种颗粒。模型各变量取值如表1所示(e=1表示球形颗粒，e>1表示长椭球形颗粒，e<1表示扁椭球形颗粒)。

由图2可知，模型1中当第二种极化体内颗粒半径a2从0.3mm增加到0.5mm和1.0mm时，其复电阻率虚分量频谱曲线的形态和频谱的变化范围与两个极化体中颗粒半径均为0.3mm时的频谱曲线形态类似，只是频谱曲线的极值向低频移动；而a2=3.0mm时，频谱曲线的形态发生明显变化，频谱的变化范围变宽；当a2=9.0mm时，频谱曲线变得更平缓，并且出现了一个次极小值。这说明当岩石含有大小不等的多种极化颗粒时，随着颗粒之间尺寸变化范围的增加，频谱曲线变得宽缓，频率相关系数值变小。

表1 三种三相GEMTIP模型参数

注：分号前面的数字表示第一种颗粒的参数取值，分号后面的数字表示第二种颗粒的参数取值。

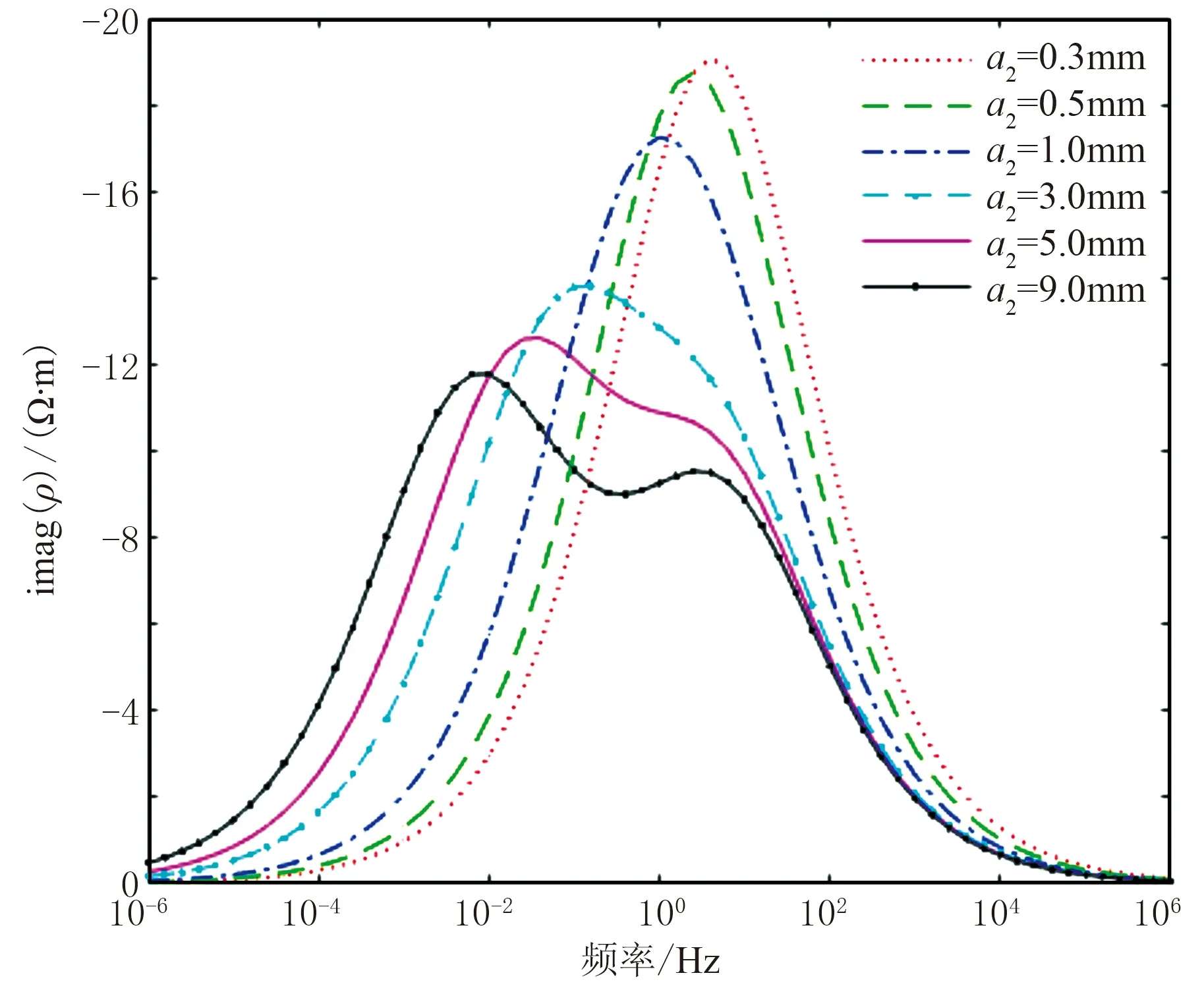
图2 模型1复电阻率虚分量频谱曲线

实际上，当岩石中的颗粒形状、大小和种类都相同时，由时间常数τp的定义式(2)可知，此时所有极化颗粒的时间常数都相等，其复电阻率虚分量频谱也如图1所示只有一个峰值的曲线，这种情况下岩石体极化的频率相关系数等效于颗粒的面极化频率相关系数。当岩石由形状和种类相同而大小不同的颗粒组成时，同样由式(2)可知，颗粒不同时，时间常数也不相等，当粒度相差较大时，颗粒的时间常数之间的差异也变大；由于时间常数决定复电阻率虚分量峰值所对应的频率，因此虚分量频谱曲线出现了多个峰值，同时使得岩、矿石复电阻率虚分量曲线变得宽缓，因而频率相关系数变小。

模型2的频率相关系数随颗粒椭圆率的变化见图3。

由图3可知，当椭球形颗粒椭圆率e2=0.5和e2=2.0时，其复电阻率虚分量频谱曲线的变化范围与两种颗粒均为球形(e1=e2=1.0)颗粒模型的复电阻率虚分量频谱曲线的差别不大，只是峰值发生了变化；随着长椭球形颗粒椭圆率的增大或扁椭球形颗粒椭圆率的减小，各个模型所对应的复电阻率虚分量频谱曲线的变化范围越来越大；当椭球形颗粒椭圆率e2=0.125和e2=8.00时，频谱曲线的变化范围比球形颗粒时变宽了很多。这说明当岩石中颗粒的形状相差很大时，其频谱曲线的频率变化范围会变得很宽，从而使其频率相关系数值减小。但需要注意的是，无论岩石内颗粒的形状怎么变，其相应的频谱曲线都只有一个峰值。同样，由椭球形颗粒GEMTIP模型复电阻率表达式(3)可以得出：岩石由含有不同形状颗粒的多个极化体构成，即矿物颗粒形状变化范围很大时，复电阻率频谱会变得更宽，因而频率相关系数会更小。

有的岩石由多种不同电化学性质的矿物颗粒组成，GEMTIP模型中面极化系数αp是与颗粒的电化学性质密切相关的参量[22,27]，含有不同面极化系数颗粒的岩石表现出不同的极化特性(图4)。

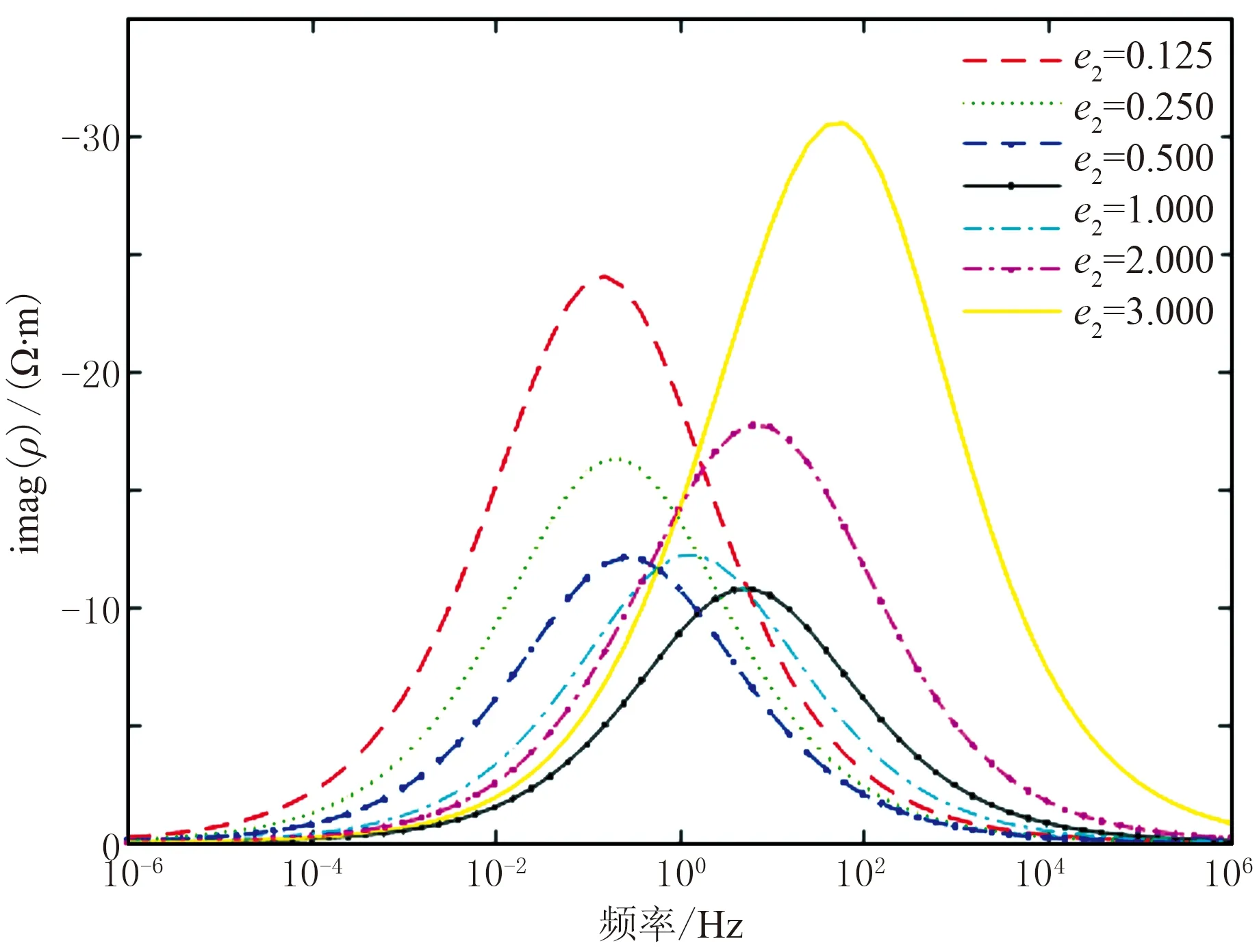
图3 模型2复电阻率虚分量频谱曲线(a1=a2=1.0mm)

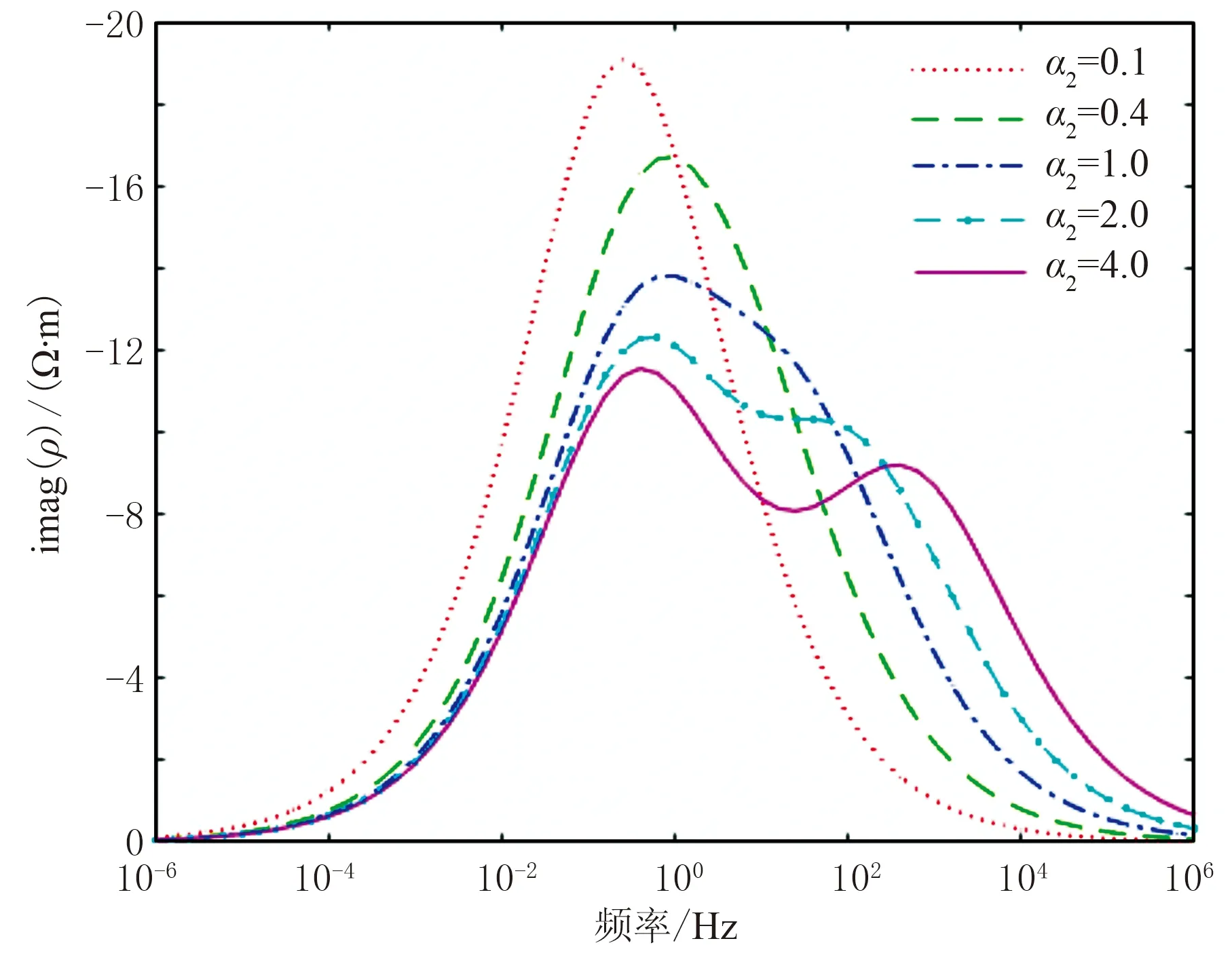
图4 模型3在α1=0.1、不同α2时的复电阻率虚分量频谱曲线

由图4可知，颗粒的面极化系数α2=0.4时，相应复电阻率虚分量频谱曲线的形态和变化范围与颗粒面极化系数均为0.1的复电阻率相差不大； 而当α2=1.0时，频谱曲线明显变宽； 当α2=2.0或4.0时，曲线变得很平缓，且出现多个极值。这说明岩石含有极化特性差异较大的多种颗粒时，其复电阻率频谱曲线变宽，从而频率相关系数变小。

频率相关系数是岩石的综合反映，前文只研究了某几个变量单独变化对频率相关系数的影响。接下来讨论多个变量同时改变对频率相关系数的作用。令模型1和模型2中两个极化体内颗粒的面极化系数α1=0.40、α2分别取0.04、0.10、1.00、2.00、4.00，计算复电阻率虚分量频谱曲线，由于篇幅所限，本文仅展示部分计算结果(图5、图6)。

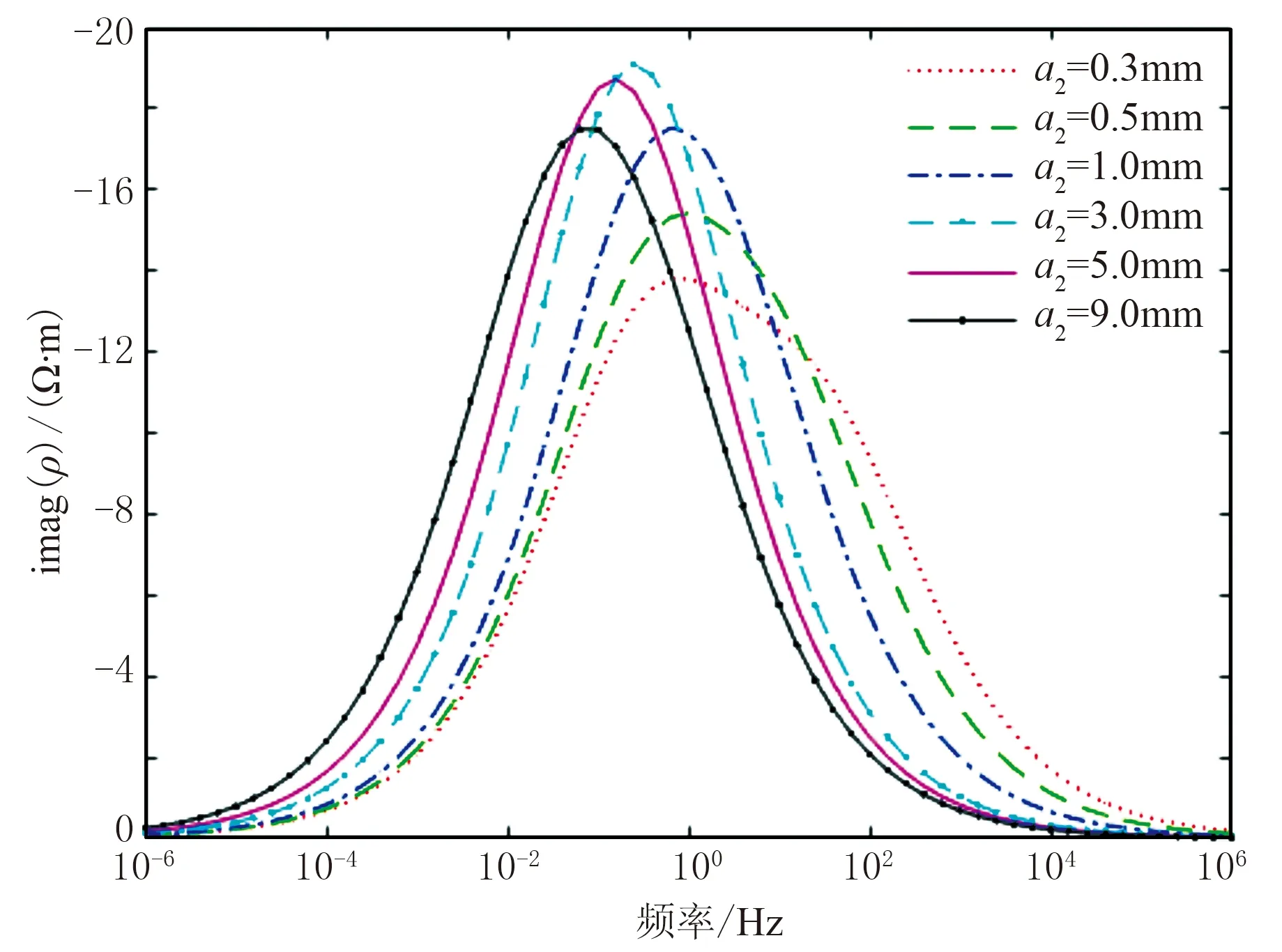
图5 α1=0.40、 α2=4.00时三相GEMTIP模型复电阻率虚分量随颗粒半径变化频谱曲线

由图5可见，对于含有不同面极化系数颗粒的GEMTIP模型而言，当α2=4.00时，随着两个极化体内颗粒的大小相差越来，模型复电阻率虚分量频谱曲线的变化范围变小，这与图2的结果相反。而面极化系数α2取0.04、0.10、1.00、2.00时，随着第二个极化体中颗粒半径的变大，模型复电阻率虚分量频谱曲线反而会变得越来越宽，这与图2的分析结果相同。这说明岩石内颗粒形状相同时，频率相关系数受颗粒的大小和面极化系数的共同影响。

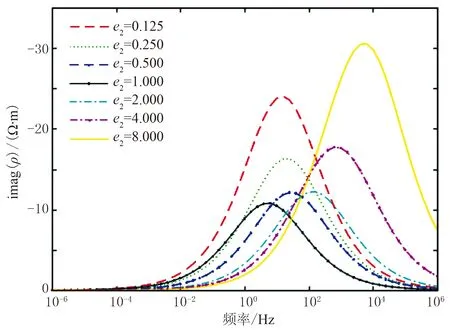
图6 α1=0.40、α2=4.00时三相GEMTIP模型复电阻率虚分量随颗粒椭圆率变化的频谱曲线

由图6可知，对于含有不同面极化系数颗粒的岩石模型而言，随着颗粒形状差异越来越大，复电阻率虚分量频谱曲线变得越来越宽，但各个频谱曲线都只出现一个峰值，这与图3的分析结果一致。多次改变第二种极化体内颗粒的面极化系数，分别取0.04、0.10、1.00、2.00，可得到同样的结论。因此，岩石中颗粒的形状差异较面极化系数的差异对整个岩石复电阻率频谱曲线变化范围的影响更大，即频率相关系数更容易受岩石内矿物颗粒形状的变化范围的影响。

当岩石由形状相同而种类和大小不完全相同的颗粒组成时，相当于岩、矿石内有多个极化体。此时由式(2)可知，极化体内颗粒的时间常数由颗粒半径和面极化系数共同决定，当岩、矿石内颗粒的半径与面极化系数的比值差别越大，颗粒的时间常数相差越大。因为时间常数决定复电阻率虚分量峰值所对应的频率[22,24]，因此虚分量频谱曲线可能出现多个峰值，这就会使岩、矿石复电阻率虚分量曲线变得很宽，从而使频率相关系数值变小，即此时岩、矿石的体极化频率相关系数小于颗粒的面极化频率相关系数。而颗粒形状的变化会引起颗粒平均半径和岩矿石结构(颗粒之间的连通情况)的变化，因此会导致颗粒之间时间常数的不同[6,13]，这会使得频谱曲线变宽、频率相关系数变小。

综上所述，当岩石中颗粒的大小、形状和种类都相同时，岩石的体极化频率相关系数等于颗粒的面极化频率相关系数，即岩石具有较大的频率相关系数。而颗粒的大小、形状和种类不完全相同时，体极化频率相关系数小于面极化频率相关系数，岩石具有较小的频率相关系数，这与诸多学者研究结果一致[8-14]。因此，当岩石内极化颗粒的极化特性相差不大时，频率相关系数主要反映岩石内矿物颗粒的形状和尺寸的变化，即矿物颗粒的均匀程度和连通情况。

4 结论

本文基于GEMTIP模型，分析了岩石含有不同大小、不同形状、不同极化特性的多种极化颗粒时的复电阻率的频率特性，得到如下结论：岩石的频率相关系数c主要受所含导电颗粒的形状、粒度和颗粒之间极化特性差异的影响。当颗粒形状、尺寸不完全相同时，随着差异的增大，复电阻率频谱曲线变得越来越平缓，频率相关系数变小；岩石含有极化特性相差较大的多种颗粒时，其频率相关系数也变小；只有当导电颗粒的大小较均匀、形状较一致和极化特性相接近时，岩石才具有较大的频率相关系数。岩石内极化颗粒的极化特性相差不大时，频率相关系数主要反映岩石内矿物颗粒的形状和粒度的变化，即矿物颗粒的均匀程度和连通情况。本文研究对于根据c值进行异常划分，并按结构区分引起激电异常的极化体具有重要的指导意义。