利用单井微地震波形能量反演震源机制
2018-09-20毛中华胡天跃
赵 炜 辛 维 毛中华 翟 尚 胡天跃 何 川*
(①北京大学地球与空间科学学院石油与天然气研究中心,北京 100871; ②中国科学院地质与地球物理研究所,北京 100029; ③中国石化石油工程地球物理有限公司胜利分公司,山东东营 257086)
1 引言
微地震监测作为非常规储层开发中一种有效的监测手段,可以提供储层改造过程中岩石破裂产生的微型地震震源位置、发震时刻、震级等大量有价值的信息[1-3]。参考天然地震震源机制相关理论可知,微地震事件的波形中还包含关于震源机制的信息,可以用于求取走向、倾向、滑动角等裂缝破裂面参数,对水力压裂储层改造效果的精细评价具有重要的意义[4-8]。
微地震观测方式一般分为三类,即井下观测、地面观测以及井地联合观测。地面观测常采用放射状布设检波器,覆盖范围广、观测方位角多、观测张角大、信号特征往往较为完备[9]。但实际应用中受到波场传播路径以及地面条件的影响,微地震信号十分微弱,有效事件一般局限于少量能量强度相对较大、信噪比较高的事件,大量能量弱、信噪比低的事件被忽略,直接导致震源机制信息相对匮乏,储层改造效果评价的有效性受到影响。与之相对应,井下观测的微地震信号信噪比较高,事件数也往往远多于地面观测,是目前应用最为普遍的观测方式。然而出于成本方面的考虑,井下通常采用单井观测方式,检波器的数量及空间覆盖范围都十分有限,导致观测张角较小、方位角单一,为震源机制求解带来极大的不确定性。
Brune[10]提出了基于扁平型裂纹的远场地震滑动辐射模式理论,是计算地震事件标量地震级的经典理论。该理论适用于剪切型震源(DC),经众多学者补充和完善[11-15],目前被广泛应用于计算水力压裂诱发微地震的震级,其局限性在于仅能求出微地震的标量地震矩,无法求解裂隙破裂面的倾向、走向和滑动角。
求解微地震震源机制,可以看作是利用有限样本(即观测资料)的某一类或某几类特征(如振幅、波形、能量、偏振、频谱等)对模式(即震源机制)进行有效识别[20]。K最近邻(K-Nearest Neighbor,KNN)分类算法是一种理论上较为成熟的模式识别方法。该方法的思路是:如果一个样本在特征空间中有k个最相似(特征空间中最邻近)样本,并且这些样本中的大多数属于某一类别,则该样本也属于这个类别。Bailey等[21]提出了一种加权K最近邻方法,根据近邻样本到测试样本的距离,将较大的权值赋给较近的近邻,使算法的稳定性大大提高。该方法简单,无需估计参数,无需训练,适合对稀有事件分类。
单井监测情况下,现有的微地震震源机制求解方法在弱信噪比条件下往往效果不理想,亟待提出一种更为有效的震源机制求解方法。本文尝试探讨微地震事件P、S波能量与裂缝破裂面参数之间的联系。以此为出发点,在计算得到震源位置及标量地震矩的前提下,采用微地震事件P、S波能量作为反演特征参数,利用加权K最近邻算法建立目标函数,反演求解微地震震源机制。为了检验方法的效果,分别应用合成微地震数据和实际资料进行测试和分析。
2 方法原理
2.1 微地震震源机制表示方法及激发的地震波
为了描述不同的地震类型,将不同方向的力矩整合为一个张量,被称之为地震矩张量[22]。地震矩张量可表示为
(1)
式中M0为标量地震矩。采用地震矩张量的9对力矩(图1)的组合可以描述所有震源类型。
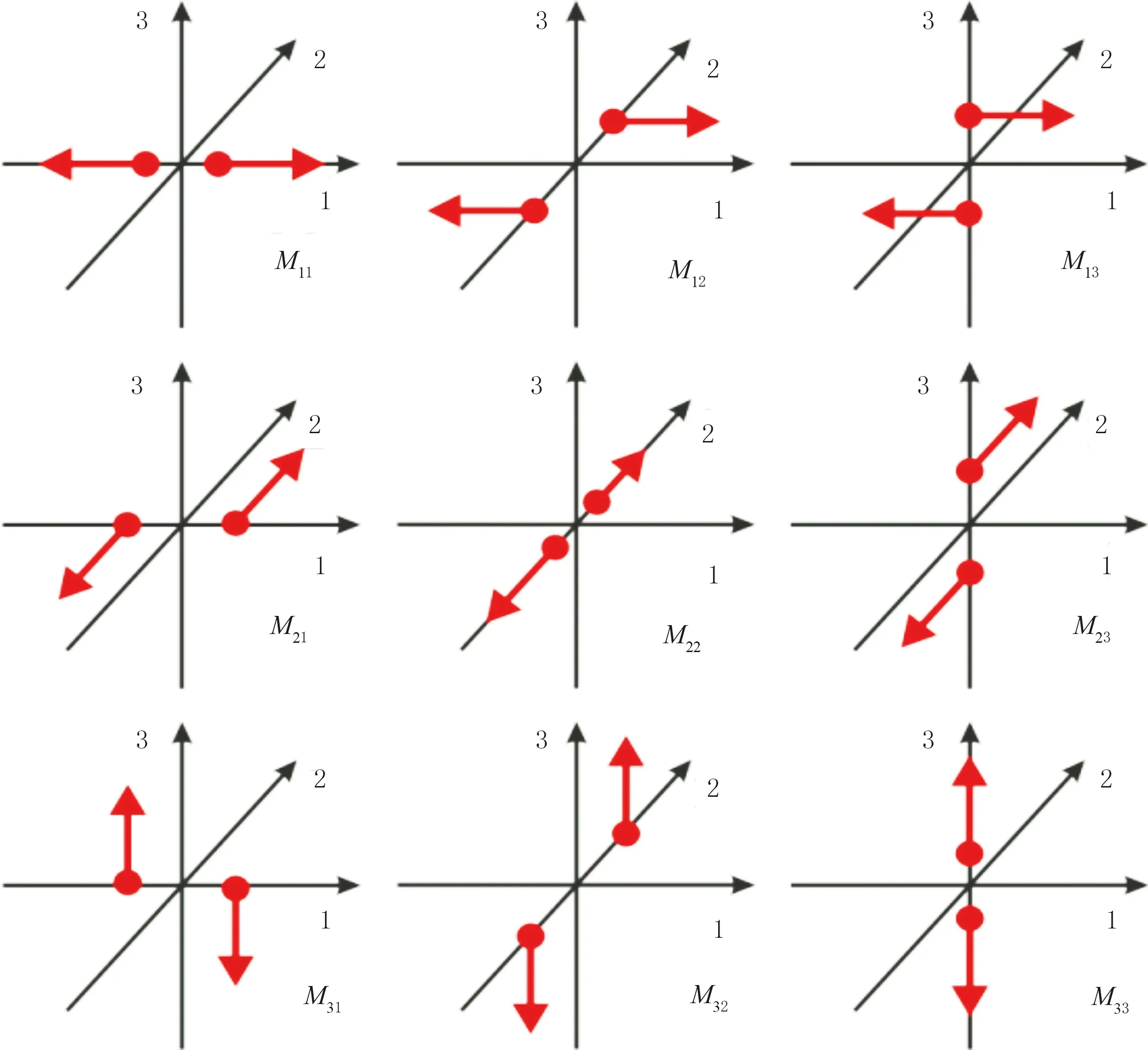
图1 地震矩张量的9对力矩[23]
根据Stein等[24]关于震源模型的假设,本文将所讨论的微震震源类型预设为DC型震源,将地震矩中待求解的6个独立分量转换为3个独立的裂缝破裂面参数, DC震源与断裂面参数的关系如图2所示,其中D为滑动量,V为断面的法向。在这一假设的基础上, DC震源的地震矩张量可以由标量地震矩M0、 断裂面走向φ、 倾角ψ、 滑动角γ计算[25]。在均匀各向同性介质中DC震源引起的地震波,Aki等[16]给出了相关的公式,经后人整理归纳,将点震源的远场波场函数与震源机制的关系定义为[26,27]
(2)
(3)
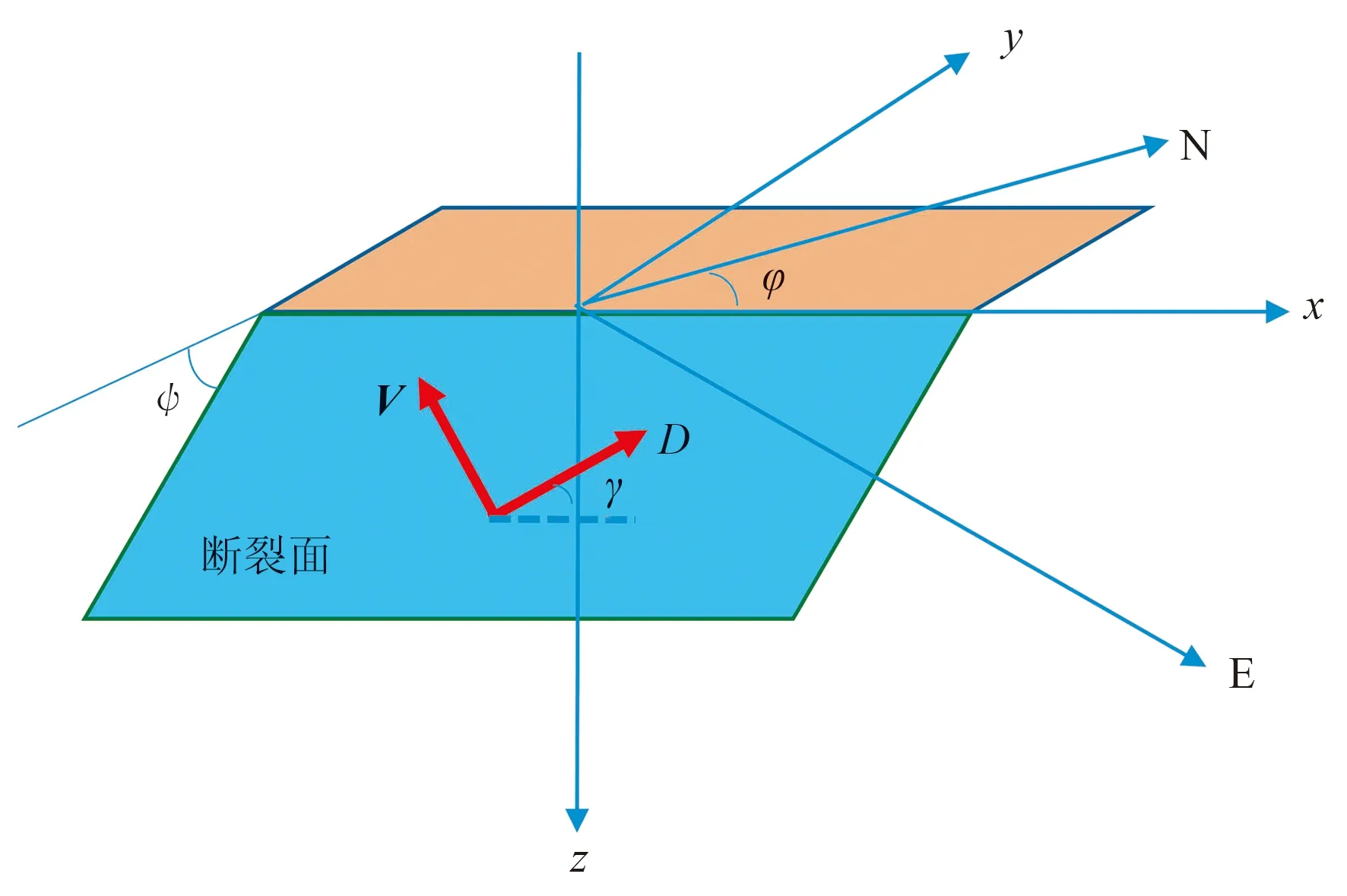
图2 断裂面参数与地震矩张量的关系[25]
2.2 S/P波振幅比方法[28,29]
S/P波振幅比方法作为求解天然地震震源机制的主流方法之一,目前被广泛应用于微地震震源机制求解。以采用S/P波振幅比方法求解震源机制为例,根据图3所示[30],将三分量检波器记录的远场微震速度信号积分转换成位移信号后,沿震源到检波器路径分解成径向与切向分量,拾取P波与横波(SH与SV波)的最大振幅AP、ASV、ASH,计算其振幅比
(4)
(5)
式中I是检波器个数。求解一组参数φ、ψ、γ,使理论计算值与实际观测振幅比的方差和最小,即为观测记录的震源机制解。

图3 三分量检波器数据旋转到P波射线坐标系
采用S/P波振幅比方法在保留S/P波振幅比值信息同时,可以有效消除检波器接收条件对波形振幅绝对值的影响,使反演过程满足均匀介质假设,具有较强适用性。然而,该方法求取单一时刻振幅比值的同时忽略了震源的强度信息,在观测方位角度单一、张角很小、有效信号微弱的单井微地震观测情况下,很容易受到噪声干扰,导致精度不高、稳定性较差[31]。
2.3 从震源机制角度对比波形能量与S/P波振幅比
微地震震源机制反演算法的关键是寻找对震源机制敏感的事件记录属性。由于井下观测检波器数量以及覆盖范围受到监测井轨迹的限制,可获得的记录数量有限,采用天然地震中常见的P波初动法求解井下震源机制会出现严重的多解性。本文尝试探讨微地震事件波形能量与裂缝破裂面参数之间的关系,并与S/P波振幅比进行对比。
假设地层模型为均匀各向同性介质,P波速度为4500m/s,S波速度为2600m/s,密度为2.5g/cm3,震源位于(0,0,2000m),观测系统如图4所示:观测井位于(300m,300m),三分量检波器共计13级,深度范围为1680~1800m,间隔为10m,微地震记录时间采样间隔为0.25ms。
首先在观测数据不含任何噪声的情况下,通过分析图5所示四种震源机制产生的模拟微地震事件能量与S/P波振幅比(图6)对目标震源机制参数的收敛情况,对两者进行对比分析。
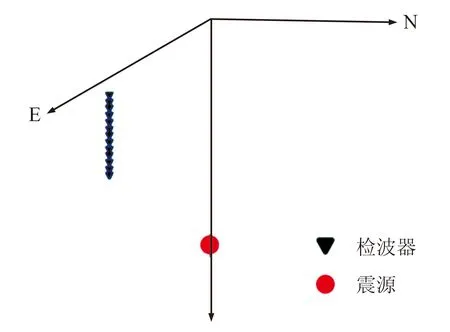
图4 单口观测井与震源位置示意图
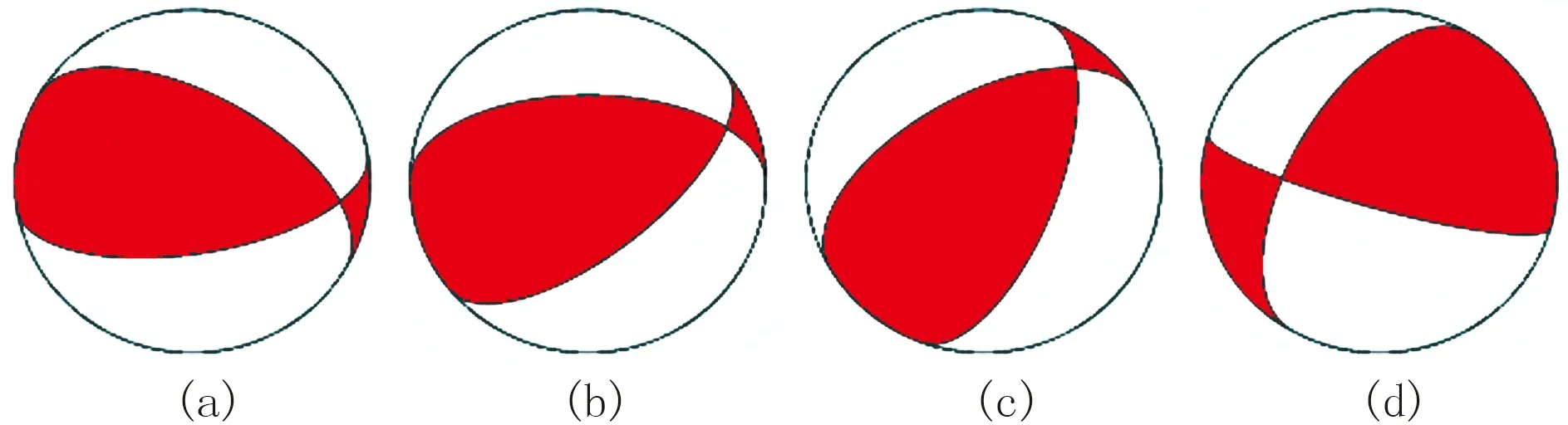
图5 不同震源机制的沙滩球
Li等[32]指出,在无其他信息的前提下,将震源机制的(φ、ψ、γ)的搜索范围分别选为(0°,360°)、(0°,90°)、(0°,180°),足以包含所有独立解。根据目标震源机制,ψ角固定在45°,对φ角、γ角所构成的区域进行网格剖分,剖分间隔均选取为5°。依据式(3)在震源位置可以获得2592(72×36)种不同的剪切震源的观测记录,再通过式(4)计算出震源机制模拟观测记录的S/P振幅比,并根据模拟记录求得相应的能量。最后根据下式计算所有震源机制与目标震源模型模拟记录的能量、S/P波振幅比之差
(6)
式中:E(φn,ψn,γn)和Q(φn,ψn,γn)分别代表搜索网格点处对应事件的能量与S/P波振幅比;E0和Q0为目标震源对应事件的能量与S/P波振幅比;n∈[1,N],其中N=n1×n2×n3,n1为φ网格剖分个数,n2为ψ剖分个数,n3为γ剖分个数,每个网格点对应一种剪切震源机制。
图6为模拟记录的能量差、S/P波振幅比差(为了方便对比,将式(6)计算的差值进行了归一化处理)随震源机制变化的分布,二者均可以收敛到真实解。采用S/P波振幅比模型解与附近的网格点差值接近,无显著差别,而采用波形能量,会在模型解附近一定范围内形成收敛梯度,收敛性优于S/P波振幅比,因此可以认为在单井观测情况下波形能量较S/P波振幅比对震源机制参数更敏感。
2.4 基于微震事件波形能量的震源机制反演算法
根据本文2.3中微地震事件波形能量对破裂面参数较为敏感这一现象,设计了一种基于微震事件波形能量的震源机制反演算法,具体实现流程如下。
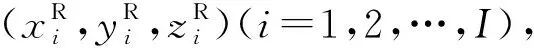
(7)
式中F为正演算子。
(2)求出网格点处模拟波场记录的波形能量。根据各个检波器的P波与S波初至信息ti,c(c=1、2,分别表示P波与S波),求出P波和S波的x、y、z分量在窗口内的能量Un,i,j,c
(8)
式中:ti,c为P波或S波的初至时间;lc为P波或S波的初至时窗长度。
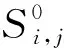

(9)
式中:wi为信噪比权重; KNN为K最近邻算法算子。
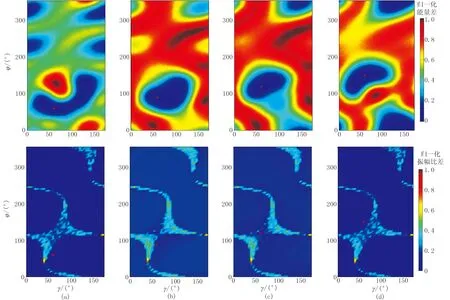
图6 四个目标震源模型的波形能量差(上)和S/P波振幅比差(下)随震源机制变化的分布
在实际研究中,不同检波器上的信噪比可能由于距震源距离或辐射花样的影响存在显著差异,因此在确定震源机制时,有必要据此对各个检波器的作用进行加权。第i个检波器的权重wi由该道信噪比SNRi确定
(10)
相比常规S/P振幅比方法,本文设计的微震事件波形能量方法在保留微地震事件S/P振幅比信息的同时,通过求取时窗内微地震事件波形能量值,保留了震源的强度信息。在求解震源机制时,输入参数从3个振幅比增加到6个能量值,增强了对反演目标的约束。此外,单井井中微地震观测系统的观测方位角单一、张角较小,所处储层通常是比较稳定的层状地层,各检波器的接收条件差别不大,因此处理实际资料时,检波器接收条件的差异对波形能量方法影响较小。另外,对时窗内各个分量的P、S波成分求取能量值,无需从波形中提取振幅比,一定程度上减轻了井中微地震观测资料S波容易受到P波续至干扰、难以提取到合适振幅比的影响,摆脱了对单一时刻振幅比的依赖。
3 模型数据处理
应用无噪声和加噪模型数据的处理结果,分析波形能量方法与S/P振幅比方法在观测方向单一、张角较小的直井观测系统下的适用性。地层模型与观测系统与2.3中相同,在进行网格剖分时,三个角度的搜索间隔均选取为15°,依据式(7)在震源位置可以得到2184(N=24×7×13)种不同的剪切震源的观测记录。
3.1 无噪声情况下两种方法反演误差对比
首先对无噪声条件下的微地震模拟记录进行震源机制反演研究。将所有的2184个不同震源机制对应的波场记录视作待求解震源机制的微震事件,采用本文提出的加权K最近邻波形能量方法进行震源机制反演。采用波形能量方法φ、γ的反演结果与模型参数存在细微误差(反演误差由反演结果与对应模型参数的角度差衡量),且误差为0的比例均在97%以上,ψ则完全一致,与采用S/P波振幅比方法反演的误差分布总体情况类似(图7)。
采用波形能量方法,在不考虑噪声情况下,出现误判的震源机制个数约占全部2184个样本总数的3%。从分布特征看,误判主要分为两类:一类如图8a和图8b所示,不同震源机制的ψ角均为0°时,φ角与γ角互为交换,这类震源有着相同的波形,约占全部误判样本个数的92%;另一类如图8c和图8d所示,不同震源机制的ψ角均为90°,φ角与γ角中一个相同,另一个分别是0°与180°或者180°与0°,引起波形极性反转,能量值相同,这种情况数量很少,约占模型测试中全部误判个数的7%。

图7 无噪声情况下采用波形能量方法和S/P波振幅比方法的反演误差分布

图8 不同震源机制波形记录的对比
不同震源机制波形相同或彼此极性反转,引起波形能量值相同,导致波形能量方法求解相应震源机制时出现误判,这两种误判情况分别是由于DC震源假设以及算法本身引起的。从前者看,DC震源假设导致震源机制求解本身具有多解性,S/P波振幅比方法同样面临这个问题,在实际情况中可以采用先验信息约束。从算法本身看,基于提取能量值的震源机制反演方法导致极性信息缺失,无法从极性角度对求解进行约束。但总的来说,误判情况占比很低(3%),对本文所提出方法影响较小。
3.2 不同噪声情况下两种方法反演误差对比
利用噪声数据分别对波形能量方法与S/P波振幅比方法进行抗噪性分析。噪声模型数据由式(7)模拟的地震波与不同幅度的随机噪声叠加而成。以事件S波初至为中心,向前、向后延拓一个短时窗,计算其信噪比。
(11)
式中:An表示随机噪声均方根振幅;As+n表示加噪后模拟地震记录S波信号均方根振幅。
分别采用波形能量与S/P波振幅比的方法,求出不同信噪比条件下2184个震源机制的倾向、走向、滑动角,并计算反演误差分布(反演误差由反演结果与对应模型参数的角度差衡量)。当信噪比为40dB时,两种方法的反演误差分布类似,都保持着很高的精度,说明在高信噪比情况下,两种方法的反演精度趋近(图9a)。随着信噪比下降,二者误差开始上升,S/P波振幅比方法总体误差上升尤为显著(图9b~图9d)。比较而言,波形能量方法的反演误差在各个信噪比条件下均低于S/P波振幅比方法,当信噪比下降到10dB时,波形能量方法误差为0°区间的样本比例仍大于50%,此时S/P波振幅比方法已经降到20%左右,且分布相对分散。可见,在同等噪声情况下,波形能量方法反演精度优于S/P波振幅比方法。
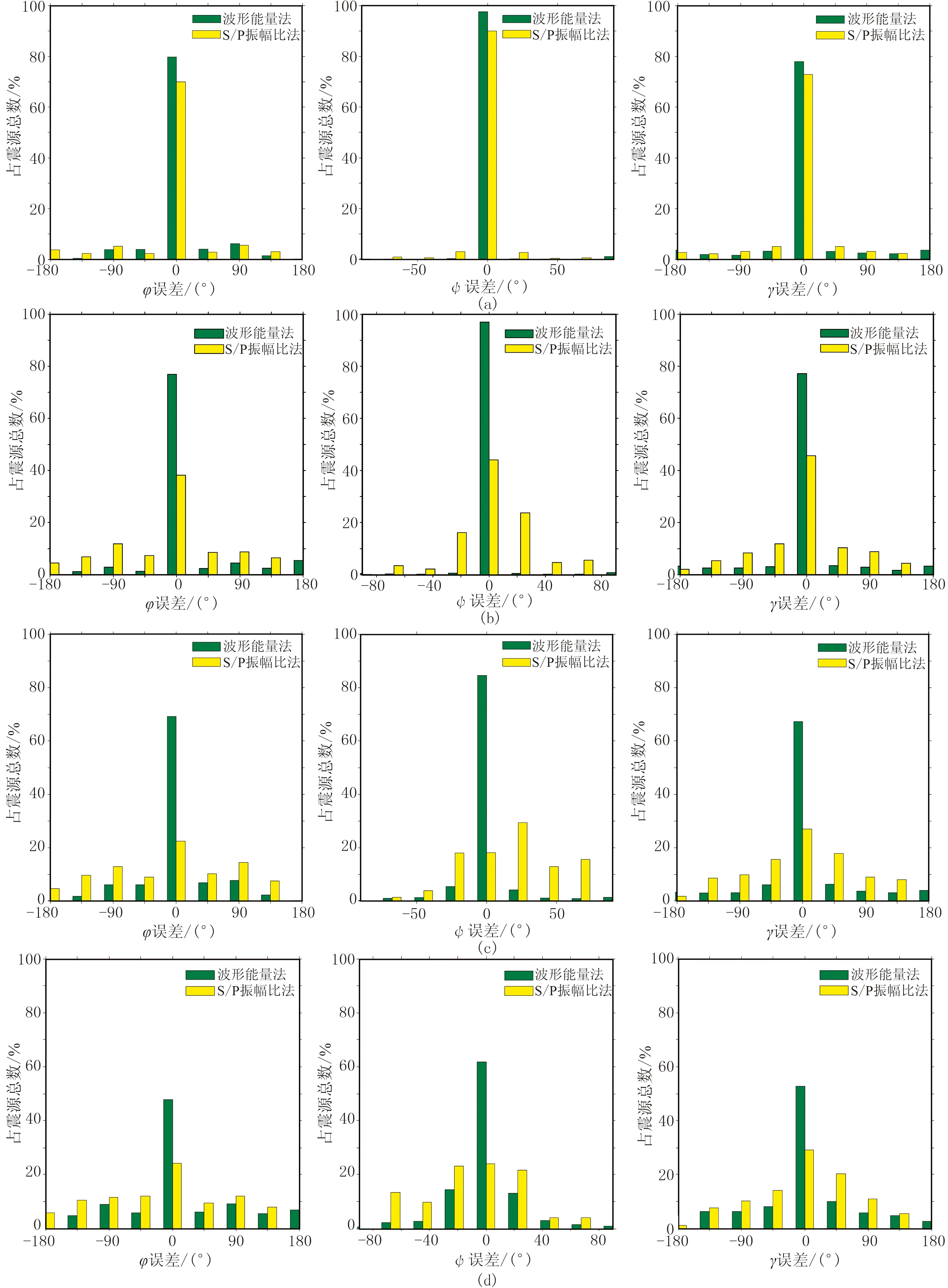
图9 不同信噪比下两种方法反演的误差分布
4 实际资料处理结果
实际资料来自于油田一口水平井第7压裂段的微地震监测数据。观测系统为一组15级井下检波器,级间距为10m,时间采样间隔为0.5ms。该观测系统布设在距第7压裂段射孔点平均距离624.34m处的一口直井中,2h15min的微地震记录中共计获得66个有效的微地震事件,逐道计算各道记录的S波信噪比(图10),信噪比集中分布在0到15dB之间。有效微地震事件经过前期初至拾取、标量地震矩反演等处理,其震源定位结果如图11所示。

图10 实际资料S波信噪比分布
采用K最近邻波形能量震源机制反演结果如图12、图13所示。分析图12可见,裂缝走向集中分布在135°左右,与压裂产生的主裂缝方向一致;裂缝倾角主要分布在15°到30°之间,为低角度缝;裂缝滑动角集中在90°附近。从沙滩球图(图13)可见,微震事件震源位置集中分布在距离射孔位置较近的东侧,并且震源裂缝破裂面走向垂直于井壁,与主裂缝延伸方向基本一致,东侧距离射孔点较远的位置存在少量滑动破裂裂缝,可能是储层压裂改造后被再次激活的天然裂缝。射孔位置的西南侧存在少量裂缝,裂缝破裂面走向大致顺着井壁。

图11 震源定位结果俯视图
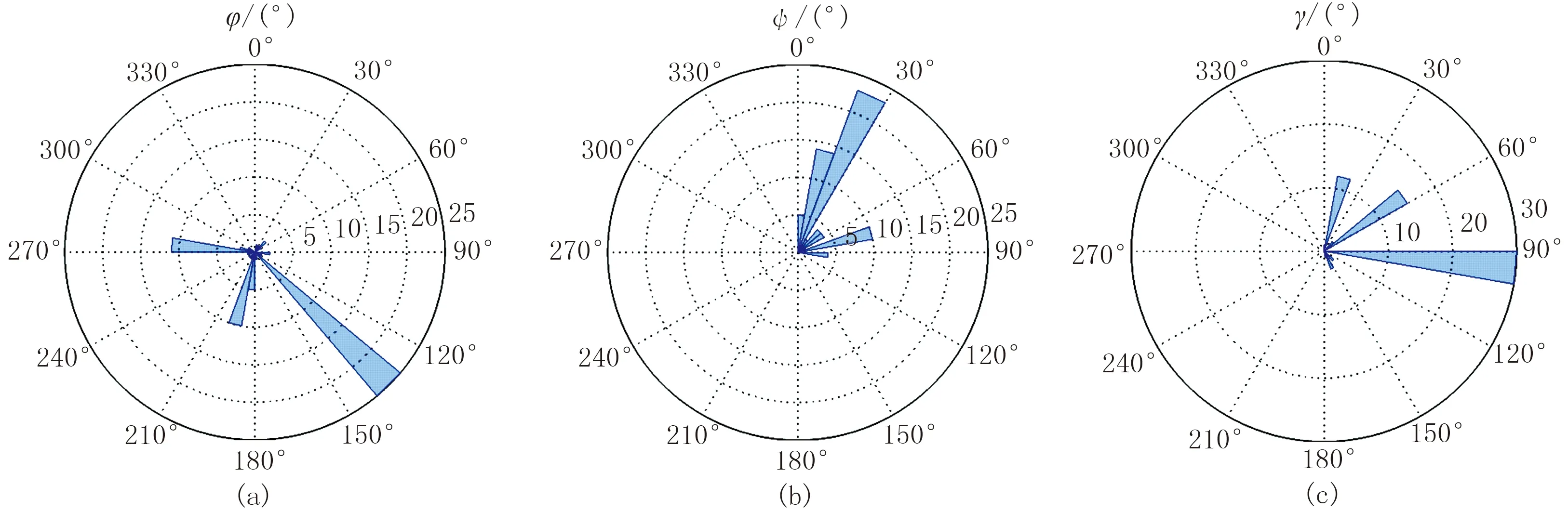
图12 实际监测数据反演得到的震源走向(a)、倾角(b)和滑动角(c)分布
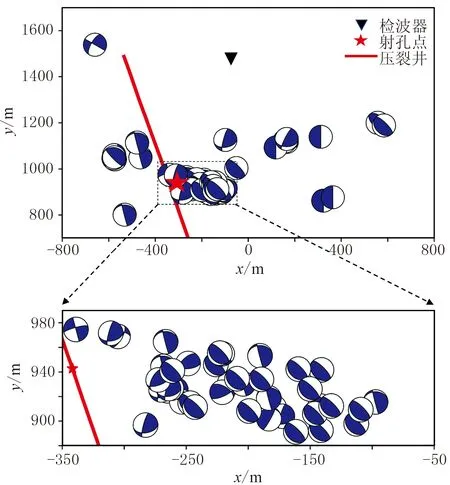
图13 震源沙滩球分布俯视图及其局部放大显示
5 结束语
研究发现,微地震事件波形能量对裂缝破裂面参数较为敏感。在此基础上,提出了一种利用波形能量改进型微地震震源机制反演方法。在单井观测系统条件下,无论模型数据还是实际数据均取得了较好的效果,证明了该方法的有效性。下一步将研究增加极性约束,提高反演准确率。
感谢中石化地球物理公司胜利分公司于静、冯刚为本文研究提供了实际监测资料,感谢北京大学地球与空间科学学院喻志超博士为论文提供了许多宝贵的建议。
