风力发电机组独立变桨控制技术仿真与试验研究

文 | 兰杰，莫尔兵，林淑，羊森林，王其君

为了实现可持续发展，风能作为一种清洁、可再生能源受到世界各国的广泛关注，已成为重点开发的能源之一。国内外大型的风电机组大多采用变速变桨技术，变速变桨风电机组的桨距角控制分为统一变桨和独立变桨。统一变桨控制，即控制系统对三套变桨执行机构执行同一桨距角指令，也是目前机组使用最多的控制方式。而随着变速变桨风力发电机组容量的增加，风轮直径越来越大，风湍流、风切变、塔影效应、偏航偏差等因素使得整个风轮面受力的不均衡度随之增强，附加载荷也越来越大，严重威胁风电机组的安全运行。独立变桨控制技术应运而生，通过优化的控制，给每支叶片叠加一个独立的桨距角信号，来降低这些附加的不平衡载荷，以提高系统运行可靠性和稳定性并延长机组使用寿命。

本文的独立变桨控制技术是将叶根应力传感器测量出来的各叶片根部的载荷及风轮方位角，通过滑环传送至所设计的独立变桨控制器以获得独立变桨期望的桨距角，最后将独立变桨期望的桨距角和统一变桨给定的桨距角之和作为风力机三支桨叶桨距角的控制量，以实现风电机组的独立变桨控制器设计，通过仿真和现场试验验证所设计独立变桨控制技术的有效性。

风轮不平衡载荷分析

实际运行的风力发电机组由于在不同方位，叶片所受载荷不同，如图1所示。

其中，My1、My2、My3为每支叶片受到的Y向弯矩，也即面外弯矩，Myq和Myd为其分解到旋转正交坐标系上的弯矩，Myaw和Mtilt为分解到静止正交坐标系上的弯矩，φ（t）为静止坐标系和旋转坐标系之间的夹角。

从图1、图2可知，若三支叶片的Myi不同，则分解产生的Mtilt和Myaw弯矩不为零，从而产生了整个风轮的不平衡载荷。

独立变桨控制要控制转速，即保证三支叶片受到的Mx总和不变，这样风轮的扭矩基本保持不变，不会影响机组的发电效率，同时要减小叶轮上不均衡载荷，仅在每只叶片上叠加一个周期变化的分量，该分量均值为零，近似呈正弦变化，在一个旋转周期内，平均变化量为零，这样就减小了旋转坐标系下的Myd和Myq，也即静止坐标系下的Myaw和Mtilt。

图1 叶片受载示意图

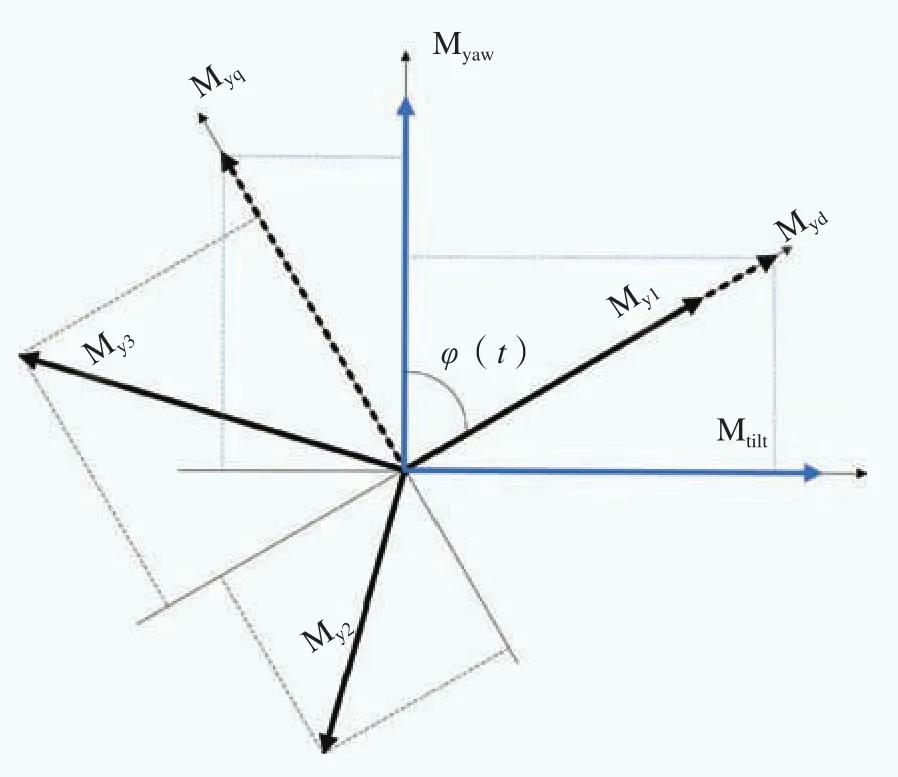
图2 三支叶片My坐标变换示意图

应对风力机运动工况和载荷工况进行分析。对风力机模型进行线性简化处理如图3所示。

叶轮上的不均衡载荷是指轮毂中心的倾覆力矩Mtilt和偏航力矩Myaw，而倾覆力矩和偏航力矩主要是由桨叶根部（载荷）挥舞弯矩Myi造成的。根据叶素理论，桨叶根部挥舞弯矩Myi为：

式中，i＝1，2，3，表示第i片桨叶，vi、βi分别为第i桨叶的有效风速和桨距角，hMy、kMy为线性化处理后的系数。

不考虑轮毂半径，轮毂中心倾覆力矩Mtilt和偏航力矩Myaw为：

图3 风力机简化模型

针对3桨叶风电机组，假定第1个桨叶方位角为φ，且桨叶处于竖直方向时φ为0，则第i个桨叶方位角为：

由此可知，当风轮转动时，桨叶在不同方位角上的风速以及其产生桨叶根部载荷变化较大。也会给叶轮造成较大的不平衡载荷。若能根据各桨叶根部载荷情况，对各桨叶的桨距角按一定的规律进行调节，是可以减小叶片根部载荷波动，进而减小叶轮上的不平衡载荷，以实现减小风电机组关键部件疲劳载荷的目的。

数学模型的建立

在充分考虑风、空气动力学、结构动力学、传动系统、控制系统等共同作用对风力机的影响后，需要一个能够模拟机组非线性载荷和动态响应的数学模型才能准确地模拟机组的动态特性。因此，一个理想的风力机数学模型如图4所示。

图4所示是一个非线性、时变、强耦合模型，很难建立其精确数学模型，而若直接将该模型用于控制器设计，控制器结构将非常复杂，且很难分析其稳定性和鲁棒性。为了满足控制系统设计的需要，需要一个线性化的数学模型，在分析机组各个环节的动态特性及其相互耦合关系后，将各个复杂的环节用一阶或二阶系统进行线性描述，最终将其线性化为一个多输入多输出系统。线性化的思路可由图5描述。

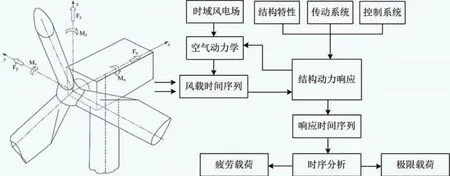
图4 非线性数学模型示意图

线性化数学模型的结构框图可表述为图6。

把上述线性化模型表式为状态空间模型形式：

式中，X为状态变量：塔架模态位移、模态速度，叶片模态位移、模态速度，以及变桨驱动器、发电机、传动系统的状态变量；

U为输入变量：风速，桨距角给定，扭矩给定；

Y为输出变量：发电机转速、发电机功率、发电机扭矩、风轮转速、齿轮箱扭矩、桨距角。

独立变桨控制器设计

独立变桨控制技术目的是为减小叶轮上的不平衡载荷，即减小轮毂中心倾覆力矩和偏航力矩。把式（1）代入式（2）可得：

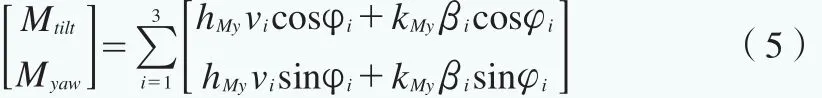
把风速vi、方位角φi作为控制器的干扰量，桨距角βi作为控制量，Mtilt和Mtyaw作为输出量（反馈量）。式（5）是一个多变量输入输出的系统，若直接基于该模型，则需要采用多输入多输出控制理论来设计控制器。LQG方法对鲁棒性较差，若采用H∞方法设计，可以处理参数鲁棒性，但是对结构鲁棒性设计较为复杂。因此考虑采用经典的PID控制进行设计，但是首先需要对模型进行解耦。

本文借鉴电机矢量控制技术中的Park变换对式（5）进行坐标变换。选用的Park变换P和逆变换P-1为：

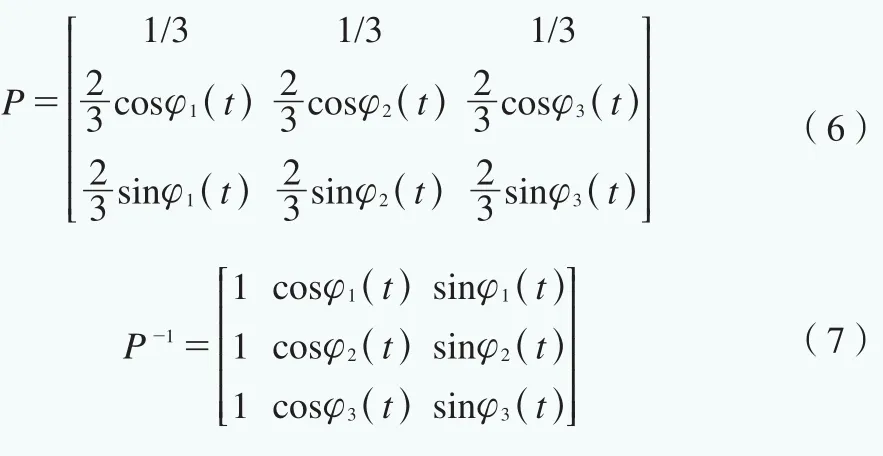
对叶片根部载荷Myi、桨距角βi、风速vi，Park变换得到：

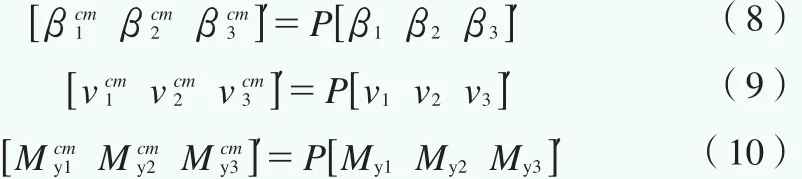
图5 数学模型线性化示意图

图6 风电机组线性化数学模型框架图

将式（8）、（9）代入式（5），可得：

把（10）带入（1），可以得到：

图7 独立变桨控制结构框图

由图7知：叶根应力传感器测量出各叶片根部的载荷，并传送给主控制器，主控制器按式（6）对叶片根部载荷进行park变换，得出Mtilt和Myaw，Mtilt和Myaw分别经控制器得到park变换坐标上的桨距角，然后再经park逆变换得出独立变桨期望的桨距角，最后将独立变桨期望的桨距角和统一变桨给定的桨距角之和作为风力机3个桨叶桨距角的控制量，以实现风电机组的控制。

表1 风力机主要参数

仿真分析

本文基于Bladed软件对所设计的控制系统进行仿真分析。风力机的主要参数如下表1所示。

仿真统一变桨控制（CPC）和独立变桨控制（IPC），结果如图8所示。

图8为独立变桨和统一变桨的叶片桨距角变化曲线，可知叶片之间的夹角为120°，各桨叶桨距角变化的相位差也为120°，理论符合设计要求。

从图9可知，独立变桨控制显著减小了叶片根部My方向的载荷波动，不仅能显著减小轮毂倾覆力矩和偏航力矩，还能减小轮毂、主轴、偏航轴承、塔架等关键部件的疲劳载荷。

在风电机组整个生命周期（20年）内，通过雨流计数法得到的风力机关键部位当量等效疲劳载荷。采用独立变桨控制有效减小了风力机各关键部位的当量等效疲劳载荷，尤其在叶片根部和轮毂中心效果最明显。

表2可知，风力发电机组采用独立变桨控制后，可显著减小叶片根部、轮毂、塔架等关键部件的疲劳载荷10%以上。

现场试验分析

在张北试验风电场对机组进行独立变桨控制技术的现场试验，验证其控制效果。独立变桨控制需要对三个叶片的根部载荷进行监测，并将监测到的应力数据通过滑环传送至主控PLC，由PLC实时计算每个叶片所需要的桨距角指令值，将指令值发送给每个桨叶驱动器，实现独立变桨控制。传感器布局方案如图10所示。

为减小风载对标定结果的影响，在风速小于6m/s时进行标定，通过将叶片置于0°和90°，使风轮至少转动一圈，利用叶片重力产生的弯矩来标定应力。

为保证现场实测数据与仿真数据一致，需要对比实际重力弯矩与模型仿真重力弯矩差别，当二者相差较小时，测量结果才能与仿真结果进行对比。

表3表明用重力进行标定，与模型之间的误差均小于5%，可认为该方案有效。进一步通过对现场采集数据进行分析，图11为现场测试风速。

图8 稳态风12m/s时桨距角变化

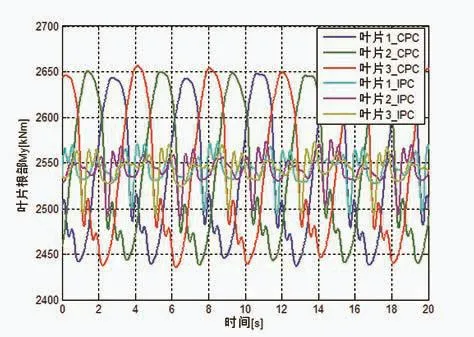
图9 稳态风12m/s时叶片面外弯矩对比

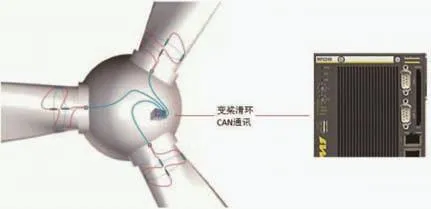
图10 叶片应力传感器布局示意图

表2 S-N slope=10 DLC1.2 工况各种控制策略疲劳损伤比较

图11 现场测风

图12 现场测试桨距角

图13 现场测试面内弯矩

表3 仿真标定误差

图12为大风情况下独立变桨控制所得的叶片桨距角实测变化曲线，可知近似呈现三相120°正弦交变，符合设计要求。

叶片旋转过程中，在旋转平面内受到气动扭矩和重力弯矩的共同作用，达到额定功率以后，气动扭矩通过变桨控制基本保持不变，而重力产生弯矩将随着桨叶方位角不同而呈现1P周期性变化，由图13可知，桨叶的面内载荷符合分析的面内载荷特征，符合设计要求。

摄影：邵明珠

图14 机组1500kW测试结果

表4 面内弯矩功率谱峰值（1P）对比

仿真与试验对比分析

试验过程中，为验证独立变桨控制降低机组疲劳载荷的效果，在同一台机组上，功率均设定为1500kW，并在基本相同的外界风况下，开启和关闭独立变桨策略。

表5 面外弯矩功率谱峰值（1P）对比

从图14结果对比可知，二者平均风速均在13m/s附近，发电机转速和电功率基本相同，风轮面内功率谱基本重合，开启了独立变桨控制策略的桨距角在1P频率附近有额外动作，风轮面外弯矩功率谱在1P频率附近有明显减小，验证了独立变桨控制器设计的有效性。

图15 机组1500kW仿真结果

为验证现场试验是否达到了表2所述仿真效果，按照图14所示的测试工况，设置Bladed仿真条件：平均风速13m/s，湍流强度B级，风力发电机组功率1500kW，分别开启和关闭独自变桨控制策略，仿真结果如图15所示。

由图14和图15面内和面外弯矩功率谱密度对比，可得表4、表5。

由表4、表5可知现场测试结果与理论仿真误差小于5%，也进一步证明了表2所述的理论计算结果的正确性，即能够有效降低风力发电机组关键部件10%以上疲劳载荷。但桨距角的动作更加频繁，变桨系统的要求也必须提高。

结论

本文对风轮不平衡载荷进行分析，建立了风力机数学模型，设计了符合风电机组运行的独立变桨控制器。通过仿真和试验验证独立变桨功能不影响机组正常运行，发电机功率和发电机转速几乎没有影响，可显著减小叶片根部My方向的载荷波动，即显著减小轮毂倾覆力矩和偏航力矩，从而减小风力机各个关键部件上的不均衡载荷，能够有效降低风力发电机组关键部件10%以上的疲劳载荷，但是频繁变桨也对变桨系统提出了更高的要求。