基于改进粒子群算法的连铸传热模型参数辨识
2018-09-20纪振平刘晓冬
纪振平,刘晓冬
(沈阳理工大学 自动化与电气工程学院,沈阳 110159)
近几年来,我国钢铁工业发展迅速,必须要不断优化连铸技术来提高产品的质量以增加销量。二次冷却动态控制是提高质量的一个重要环节,其中连铸传热模型参数辨识是优化连铸的关键。Miziker[1]采用数值法求解传热微分方程,并进一步开拓,使计算机在铸坯凝固过程中的应用得到了迅速发展。Spitzer等[2]通过结晶器出口以下的铸坯表面的实际测量温度,在线调整结晶器内的传热系数,使计算温度与实测温度相吻合。罗森[3]利用有限差分方法建立了在非稳态时二维连铸坯在线实时温度场计算模型。随着人们对凝固传热过程的不断改进与优化,发现二冷区铸坯表面换热系数的反算是一个比较困难和复杂的问题。首先,铸坯表面的实际温度由于条件限制很难测量;其次,二冷区铸坯表面换热系数的辨识具有非线性、不确定性和计算量大等缺点。张晓博[4]以板坯连铸机为研究对象,并基于热成像测温原理建立连铸二冷传热系数的反算模型,得出二冷换热系数与水流密度的关系表达式,采用射钉法对反算模型进行了验证,具有很高的准确性。李朝霞等[5]通过分验法和试验与计算相结合的逆向法确定了铸造铸锭与冷却水之间传热系数,并分别分析了两种方法的优缺点和冷却水对换热系数的影响因素。廖建云等[6]建立了铸坯表面热交换系数方程,并通过实验测定的数据回归,得到铸坯表面热交换系数与铸坯表面温度及水流密度函数关系式,即喷嘴的热态性能。Santos等[7]以小方坯为研究对象,基于红外高温测温仪的实测数据,建立了铸坯凝固导热反问题数学模型,采用有限差分法和自动搜索原理对二冷区铸坯的表面换热系数进行计算。
随着智能技术的发展,粒子群算法(Particle Swarm Optimization,PSO)已经逐渐被应用于各个领域。PSO算法提供了一种通用框架来求解复杂系统优化问题,并且因为其需要调节的参数较少,简单且易于实现的优点,被广泛应用于各个领域。日本的富士电力公司的研究人员将电力企业问题简化为函数优化问题,并使用改进的PSO算法进行优化求解,实验结果表明了PSO算法在处理该问题上存在着一定的优势。美国的一家公司在各种生物化学成分的优化组合上已经成功的采用了PSO算法,并人工合成了微生物。G.Ciuprina等于2002年提出了一种智能PSO算法,并将其应用于解决电磁学上线圈尺寸优化问题[8]。
本文以连铸凝固传热模型为基础,通过改变拉速和过热度以及二冷区水量,以PSO算法对二冷区四段换热系数进行反算,并验证辨识参数的可靠性。
1 二冷换热系数反算模型的建立与计算流程
1.1 二冷换热系数反算模型的建立
连铸二冷区各段换热系数与水流密度的关系根据不同的喷淋方式由不同的经验公式确定。
1)喷水冷却[9]:
(1)
2)气雾冷却:
h=1000w/a
(2)
式中:w为水流密度,L/(m2·s);a为待辨识参数;Tw为冷却水温度;h为换热系数。
由于铸坯在传热过程中大致具有对称性,所以选取铸坯的四分之一断面作为研究对象,根据凝固传热原理,建立凝固传热模型,并根据混沌粒子群(Chaos particle swarm optimization,CPSO)算法编程,开发连铸板坯二冷换热系数反算的数学模型。
1.2 二冷换热系数反算模型的计算流程
二冷换热系数反算模型依据凝固传热原理,将换热系数a0赋予初值,调用凝固传热模型,改变拉速、过热度进行温度场的计算。将得到的温度场与测点处的实际温度相比较,迭代次数不断增加,直到适应度函数f(x)趋近于零,此时便认为计算温度与铸坯表面实际温度基本无误差,则a0也被认为是最接近实际工况的二冷换热系数,停止迭代。该模型不仅能求解出连铸过程中各二冷区的换热系数,还能得到铸坯表面的温度场分布[10]。图1为二冷换热系数反算流程图。
2 基于混沌粒子群算法辨识模型参数
本文采用混沌粒子群算法对目标函数(1)进行优化,根据得到的测量数据和计算数据,定义优化目标为

图1 二冷换热系数反算流程图
(3)
式中:J为目标函数;ai为辨识参数;k为二冷区分段数;m为自然数,取值为1,2,3,4;Tmes、Tcal分别是铸坯表面实际温度和根据传热模型得到的计算温度。最终得到的最优解为参数辨识结果。
2.1 标准粒子群算法
PSO算法是一种模拟鸟群觅食行为的过程。在一个D维的目标搜索空间中,每个粒子的速度更新是由两个因素来决定的,即个体极值和全局极值。在每一次迭代中,粒子通过跟踪这两个极值不断更新自己的位置来找到最优解。粒子速度与位置更新的表达式为
vi,d=wvi,d+c1r1(pi,d-xi,d)+c2r2(gd-xi,d)
(4)
xi,d=xi,d+vi,d
(5)
式中:i为粒子编号;w为惯性权重;c1、c2分别为认知学习因子和社会学习因子(正常数);r1、r2为[0,1]范围内的均匀随机数;pi,d为粒子i历史最优位置;g为群体中所有粒子经历的最优位置。
2.2 混沌粒子群算法
通过分析式(4)和式(5)可知,随着迭代的不断进行,当某些粒子逐渐更新到自身历史最优位置时,这些粒子的更新速度逐渐减小并趋近于零,此时粒子很可能陷入局部最优,粒子出现停滞状态。为避免粒子群出现局部聚集状态,帮助粒子群跳出局部极值,提高粒子群的全局寻优能力和寻优效率,使得粒子群能很快的收敛于全局最优,引入混沌机制使粒子进行位置更新。混沌运动在其混沌吸引域内是各态历经的,且又满足粒子群初始化的随机性要求,混沌算子能加快收敛速度,弥补收敛精度。所以利用混沌机制的这一特点,在初始化种群位置和速度时,采用一种经典的混沌映射—Logistic映射,与具有较好混沌扰动能力的Tent序列相比,Logistic映射的全局遍历性能更好。
利用Logistic映射迭代产生的混沌序列,其表达式为
yk+1,d=4yk,d(1-yk,d)
(6)
其初始值y0各分量随机产生,y0,d∈(0,1)。
计算适应度f,当粒子i连续NC次满足|f(xi)-f(pi)|<δ时即判断粒子处于“停滞”状态,将粒子“激活”,通过类似载波方式将粒子的“活动空间”扩大到一个以当前粒子位置为中心、Rd为半径的区域:
(7)

3 仿真结果与分析
3.1 基于四点温度反算四点辨识参数
在辨识参数范围[0.5,10]内,随机给四个辨识参数a1、a2、a3、a4赋值,通过不断改变拉速和过热度,得到铸坯表面的温度场;将计算得到的温度场与实际表面温度进行对比,通过混沌粒子群算法进行参数辨识,使得适应度函数的值趋近于零,观察此时的铸坯表面温度是否与计算得到的铸坯表面温度存在误差,取温度误差最小的四个辨识参数,并与设定的参数进行对比,验证辨识参数是否可靠。
本文进行了大量的实验来对二冷换热系数反算模型进行验证,取其中的一组数据。
假定四段换热系数为a1=2.3,a2=2.6,a3=3.2,a4=3.8。表1、表2为同等迭代次数、相同拉速和过热度下,基于基本粒子群和混沌粒子群得到的辨识参数及温度误差。

表1 基本粒子群辨识参数及温度误差

表2 混沌粒子群辨识参数及温度误差
图2为迭代次数50次、过热度为10℃、拉速为2(m/min)时基本粒子群和混沌粒子群收敛过程。此时wmin=0.1,wmax=0.9,c1=1.3,c2=1.7,M=50,其中M为迭代次数,通过表1、表2的对比以及图2,可以看出,基本粒子群易陷入局部最优,出现早熟现象。混沌粒子群算法由于混沌机制的引用,在第26次迭代时跳出局部最优并迅速收敛,最终得到最优解,辨识参数误差较小,验证了混沌粒子群算法辨识的可靠性。
3.2 根据三点温度反算四点辨识参数
在连铸过程中,由于现场条件限制,二冷区一段末的表面温度无法测量,此时需要利用已知的二冷区后三段末端的温度来辨识准确的四个二冷换热系数,从而得到准确的二冷区一段末的表面温度。根据二冷换热系数与水量的关系研究[11],加入约束条件辨识参数a1、a2小于a3、a4,连铸二冷区四段换热系数仍然设定为a1=2.3,a2=2.6,a3=3.2,a4=3.8。并对混沌粒子群中的学习因子c1、c2和惯性权重ωi进行限制,以求找到二冷换热系数的最优解。文献[12]认为当c1、c2的和小于3时优化的效果最好。通过采用异步变化策略因子,使粒子能更多的向社会最优解学习,而较少的向自身最优解学习,使粒子有很快的收敛速度并保持粒子多样性。惯性权重ωi和学习因子c1、c2限制如下:

图2 PSO和CPSO收敛过程
ωi=ωmax-((ωmax-ωmin)/Mmax)i
(8)
c1=c1i-(c1i-c1f)(k/Mmax)
(9)
c2=c2i-(c2i-c2f)(k/Mmax)
(10)
式中:c1i、c2i分别为c1、c2的初值;c1f、c2f分别为c1、c2的迭代终值;k为当前迭代次数;Mmax为最大迭代次数。表3表示有约束条件的混沌粒子群辨识参数。图3为有约束的CPSO收敛过程。
此时的参数wmin=0.4;wmax=0.9;混沌粒子群适应度函数f2=1.53×10-7,通过加入约束条件a1、a2小于a3、a4,使得在未能测到二冷区一段末表面温度的情况下,能够准确得到二冷区换热系数,从而得到准确的温度。
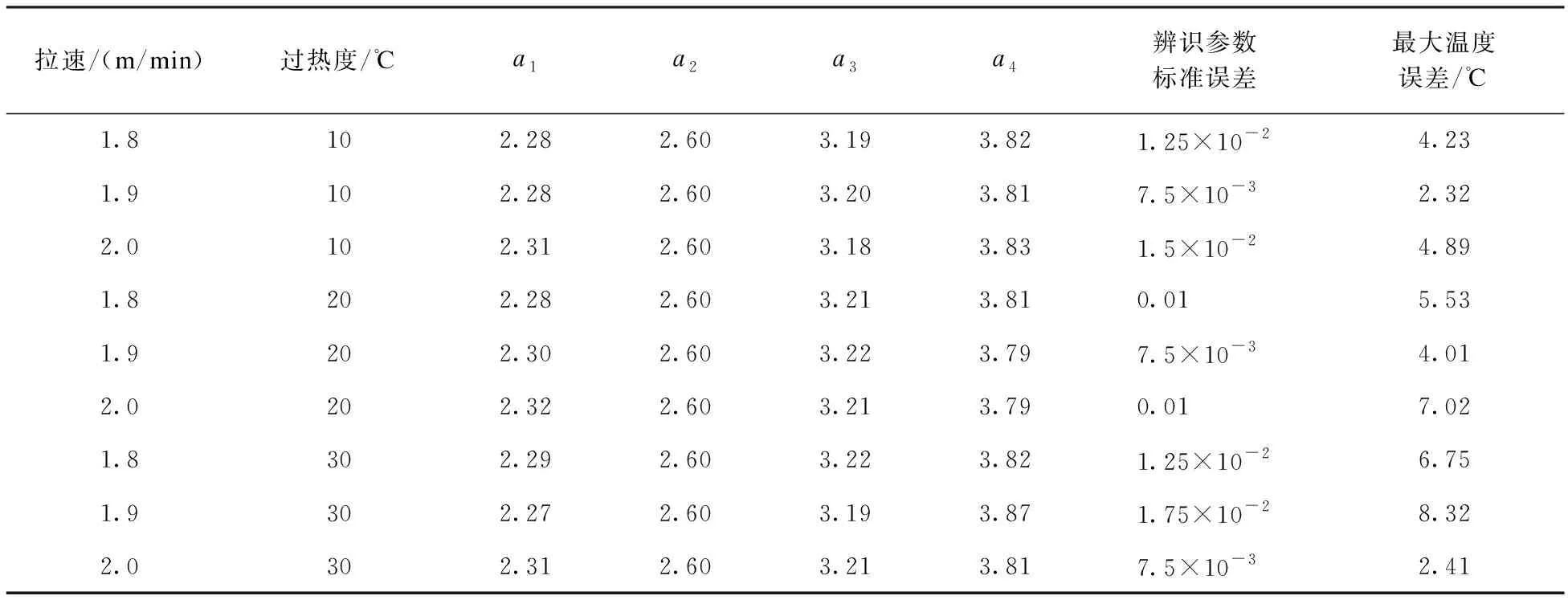
表3 有约束混沌粒子群辨识参数

图3 有约束CPSO收敛过程
4 结束语
通过采用混沌粒子群对连铸二冷换热系数进行辨识,简单有效且收敛速度快,混沌机制的引用增强了粒子的全局寻优能力和寻优效率;通过建立二冷区换热系数反算模型,将辨识得到的参数与设定的参数进行对比,通过混沌粒子群辨识得到的参数误差小,且计算温度与实际温度偏差小于3℃,验证了辨识参数的可靠性,满足工程应用。基于混沌粒子群算法用已知的三点温度辨识四段二冷区的换热系数,可以较好的解决由于工况限制而无法测量部分二冷区的实际表面温度,从而导致参数辨识不准确的问题。
