连铸坯矫直的有限元分析

刘克仲 闫 冬

(1.天津重型装备工程研究有限公司，天津300457;2.一重集团天津重工有限公司，天津 300301)

连铸坯矫直的有限元分析

刘克仲1闫 冬2

(1.天津重型装备工程研究有限公司，天津300457;2.一重集团天津重工有限公司，天津 300301)

利用有限元技术模拟了连铸坯的矫直过程，获得了矫直过程中连铸坯的温度分布、受力分布等数据，对分析连铸坯缺陷产生原因以及质量改进提供数据支持。

连铸坯;矫直;有限元模拟

连铸坯目前仍然存在宽面纵裂、窄面凸出及内裂等质量缺陷，分析矫直过程中连铸坯温度分布及应力应变的分布对改进铸坯质量有着重要意义。在实际生产过程中，连铸坯温度较高，内部存在液芯，进行全过程、动态的数据监测较复杂，可行性不高，利用有限元软件进行数值模拟可有效解决此问题。

1 连铸坯矫直模型的建立

1.1 矫直辊中心坐标的确定

某钢厂的连铸设备参数如图1所示。铸坯的规格为1 000 mm×237 mm，铸坯矫直段的半径为9 300 mm，拉坯速度为 1.5 m/min，矫直辊直径310 mm，辊距为380 mm，铸坯进入矫直区之前经过的弧长为13 300 mm。

根据钢厂的实际设备参数，取部分矫直前圆弧区辊列、连续矫直区辊列及后续直线区辊列为研究对象，计算得到各辊的中心坐标见表1。

连铸坯矫直模型中铸坯圆弧区的圆心坐标是(762.8，9 584)mm，半径 R 为9 300 mm。

1.2 连铸坯网格的划分与材料选取

图1 连铸机设备参数Figure 1 Equipment parameters of continuous caster

表1 矫直模型的辊子中心坐标Table 1 Center coordinates of straightening model roller

选取即将进入矫直区一段的铸坯为分析对象，由于六面体的良好受力传递特性，铸坯全部划分为六面体网格，见图2。选取铸坯段共划分成12 800个网格，节点15 309个。

1.3 建立矫直模型

铸坯由接触面的摩擦力带动前行。定义接触控制及高级接触控制，选择摩擦类型，确定接触探测时的接触容限和偏斜系数以及分离力等重要参数，建立矫直模型如图3所示。

图2 铸坯的网格划分Figure 2 Grid division of casting blank

图3 矫直模型图示Figure 3 Illustration of straighteningmodel

2 数值模拟

2.1 矫直前铸坯温度分布

铸坯进入矫直前的温度分布见图4，表面温度在950℃左右，铸坯的角部温度较低，约为800℃。铸坯中心部分温度较高，约为1 450℃，处于材料的固相线与液相线之间。

图4 铸坯的温度分布假设Figure 4 Temperature distribution assumption of casting blank

2.2 矫直过程的条件简化

(1)铸坯在矫直过程中存在宽面的对流换热、窄面的对流换热，垂直铸坯运行方向假设为绝热面，加载边界条件如图5所示。

(2)矫直过程中矫直辊为不变形刚体。

2.3 矫直模拟

本次数据模拟共300个增量步，为了形象的表示模拟过程，分别取增量步为100、200和300时的铸坯矫直状态，见图6。

通过模拟，铸坯经过矫直区后得到了矫直，验证了利用有限元软件模拟的正确性，铸坯在矫直过程的温度及力学参数为进一步改进铸坯质量提供参考。

图5 铸坯的边界条件Figure 5 Boundary condition of casting blank

3 模拟结果分析

3.1 应力分析

铸坯在矫直过程中，由曲变直，内弧侧受拉力，外弧侧受压力。在236增量步时选取铸坯厚度方向自上至下的一列节点作为分析研究对象，从结果文件中提取等效应力分布，见图7。

图6 矫直模拟过程状态Figure 6 Straightening simulation process status

可以看出，铸坯内弧侧与外弧侧表面上等效应力较大，且内弧侧最大等效应力稍大于外弧侧［1］。矫直应力向铸坯中心方向逐渐减小，铸坯中心处最小。

3.2 应变分析

应变反映了铸坯在矫直过程中的变形速度，在铸坯上选取处于不同部位的213、224、231节点为研究对象，分析它们从矫直初始至矫直结束的应变变化，提取应变结果如图8所示。

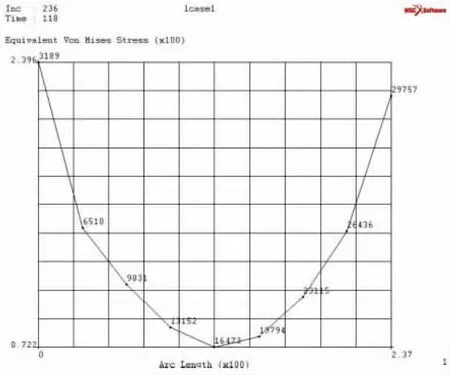
图7 等效应力分布图Figure 7 Equivalent stress distribution chart

可以看出，铸坯在矫直初始阶段与矫直末端应变速率很小，矫直过程中应变接近线性变化，铸坯与矫直辊接触的瞬间应变产生突变，因此若采用矫直辊密排技术，可有效减小突变，对提高铸坯质量有很大益处。

3.3 温度场分析

在矫直过程中，对流换热使铸坯温度不断降低，为了更好的观察温度分布情况，沿铸坯行进方向做切片显示，见图9。铸坯温度中部较高，外侧逐渐降低，角部温度最低。同实际情况相吻合，验证了模拟的合理性。

图8 铸坯不同节点的应变图Figure 8 Various nodes strain chart of casting blank

4 结语

本文结合某钢厂实际设备参数，建立了连铸坯的矫直模型并成功模拟了连铸坯的矫直过程，得到了矫直过程中的应力应变与温度等重要数据，为今后改善连铸坯的质量提供了参考和依据。

图9 铸坯的温度切片显示Figure 9 Temperature slice appearance of casting blank

［1］刘立文.有限元法在连铸工艺中的应用.钢铁研究总院，2000:35－38.

编辑 傅冬梅

Finite Element Analysis of Continuous Casting Blank Straightening

Liu Kezhong，Yan Dong

Straightening process of continuous casting blank has been simulated by finite element technique and relevant data in the process of straightening has been obtained，such as temperature distribution and force distribution，which provided data basis for analyzing continuous casting blank defects origin and quality improvement.

continuous casting blank;straightening;finite element simulation

O242.21

A

2013—07—04