考虑广告和回收策略的闭环供应链研究

曲铁平,彭 涛

(1.沈阳理工大学 理学院,沈阳 110159;2.沈阳市第56中学,沈阳110141)

在考虑回收的闭环供应链中,废旧产品再制造对于节省经济成本、环保和可持续性发展等方面的作用已被大众认可[1]。近些年来,由于环境保护法的不断出台和世界范围内资源短缺的现状,越来越多的工业链实施废旧产品回收再制造的做法,如汽车零部件、照相机、打印机等制造行业。为使再制造更有效的实施,一个重要的环节是逆向回收渠道的有效管理。广告作为拓展市场的重要工具,其在闭环供应链中的作用不可忽视,做好广告不仅可刺激消费者需求,还可有效提高废旧产品的回收率[2]。

Huang M等[3]研究了闭环供应链中零售商回收与第三方回收的逆向物流回收竞争,并考虑了二者的竞争强度对供应链的影响。文献[4-5]研究了考虑公平和需求扰动因素下的闭环供应链定价问题。Rahman等[6]考虑了政府采取法规对电子产品回收制定的激励机制,以及此机制对闭环供应链回收决策的影响。Mcalister[7]通过研究得出广告投资可使消费者产生品牌意识,从而增强消费者心理对产品的品牌效益。

然而,现有的回收再制造文献中关于广告对提高废旧产品回收率方面的研究还较少,因此,本文在制造商负责回收的闭环供应链中,将制造商作为斯坦伯格博弈模型的主导者,考虑广告投资,以供应链各参与方利润最大建立模型,得出最优解;分析供应链中各参与方定价和回收率决策,以及广告投资对各参与方定价、废旧产品回收率、消费者需求及利润的影响。并根据市场参数得到最优的广告投资表达式。

1 问题及模型

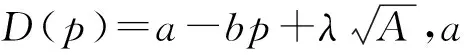
可以得出制造商和零售商的利润模型如下。

(1)

(2)

在模型(1)和(2)中,决策变量是批发价w、回收率τ、零售价p和广告投资A;其余均设为已知参数。由于假设制造商是供应链中的斯坦伯格博弈领导者,所以先由制造商决策产品的批发价w及回收率τ,再由零售商决策零售价p以及广告投资A。

2 模型求解及结果分析

由经典的斯坦伯格博弈模型,给定批发价w和回收率τ后,由零售商的利润模型求出最优零售价p*与w、τ的函数关系,再回代到制造商的利润模型中,由制造商决策出最优批发价w*和最优回收率τ*,这样便得出最优批发价w*、最优回收率τ*和最优零售价p*关于广告投资A的表达式关系,最终以零售商利润最大为目标,得出最优的广告投资A*。

定理1在市场参数选取适当时,模型中零售商的利润函数πr关于零售价p和广告投资A是严格凹的函数,因此模型有最优解。

证明:先求出利润函数πr关于决策变量p和A的二阶海赛阵H。

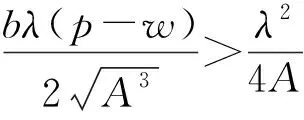
定理2给定广告投资A时,最优批发价w*、回收率τ*和零售价p*关于广告投资A的表达式为

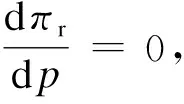
(3)

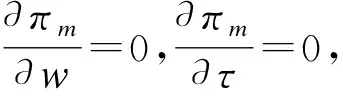
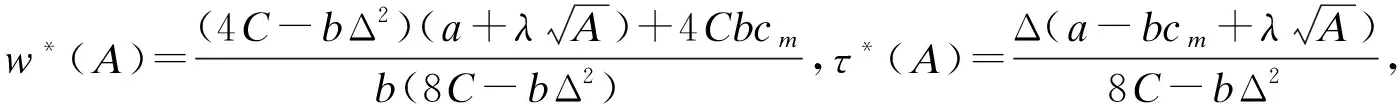
从定理2的最优解解析表达式中可以得出,制造商和零售商的决策变量受广告投资的影响。

定理3制造商的最优批发价w*,最优回收率τ*,以及零售商的最优零售价p*均随广告投资的增大而增大。

定理3的结果符合现实意义,尤其是较为贵重的电子产品,如电脑、高档手机等,零售商需要一定的广告投入以刺激消费者的需求,增强电子产品的品牌效益,进而可提高零售价;另一方面,增加的市场需求可以诱使制造商提高批发价,并且扩大的市场需求也会直接促使有较高的废旧产品回收率。

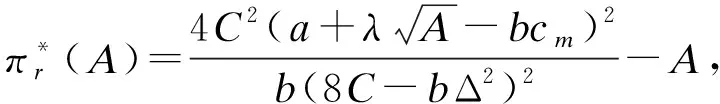
4 结束语

在考虑零售商广告投资的闭环供应链中,由制造商负责回收并作为渠道领导者,零售商作为跟随者,以供应链各参与方利润最大建立模型得出最优解,通过最优解发现制造商的最优批发价w*、最优回收率τ*、以及零售商的最优零售价p*均随广告投资的增大而增大,但零售商利润不与广告投资A成单调关系,零售商可根据市场参数来确定最优的广告投资。