一类Kuramoto Sivashinsky方程的显式解

连颖颖,王宏伟

(安阳师范学院数学与统计学院,河南安阳 455000)

1 引言

在研究空间三维Belousov-Zhabotinski型反应扩散系统的角相位湍流时,Kuramoto[1]导出了如下一类四阶Kuramoto Sivashinsky(KS)方程

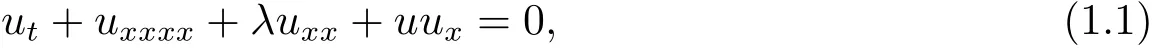
其中u=u(x,t)是未知函数,λ＞0被称为反扩散常数.这个方程也被Sivashinsky[2]用来研究空间二维层焰面的微热扩散不稳定性问题.此外,该方程在其他领域还有广泛的应用[3].近年来,该方程的很多性质被广泛研究[4–6],如非平凡解的分岔与稳定性、吸收集半径、渐近吸因子、零解的可控性、时间离散化与稳定性区域等.

本文将在半无界区域上研究如下一类KS方程的初边值问题

KS方程Cauchy问题的研究已有很多结果[7–9].而初边值问题的适定性和数值计算至今尚未解决.本文将采用近年来在相关领域内提出的新的一致变换方法(UTM)来研究方程(1.2)的显式解,这个方法的最新进展参见文献[11–13].利用UTM方法得到的显式解的公式,可以为后续KS方程初边值问题的适定性和数值计算的研究提供新的思路.

本文的主要结论由下面的定理给出.

定理1初边值问题(1.2)的显式解是

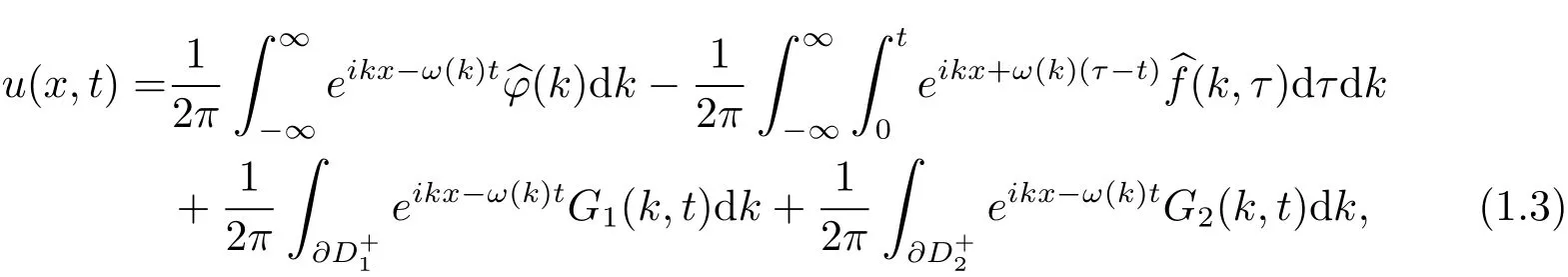
2 显式解的推导过程

假定v(x,t)=eikx−ω(k)t是方程vt+vxxxx+vxx=0的一个解,代入方程中得到KS方程的象征关系式ω(k)=k4−k2,ω(k)在显式解的求解过程中起着关键的作用.

首先把方程写成散度形式,这样做的目的是便于使用Green公式.设u(x,t)是方程(1.2)的解,则

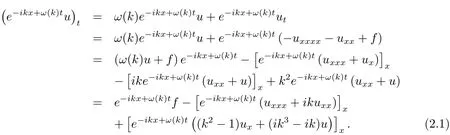
(2.1)式就是和(1.2)式等价的散度形式的方程,把它称为方程(1.2)的局部关系等式.

将(2.1)式在区域D={x≥0,0＜t≤T}上作二重积分,得到

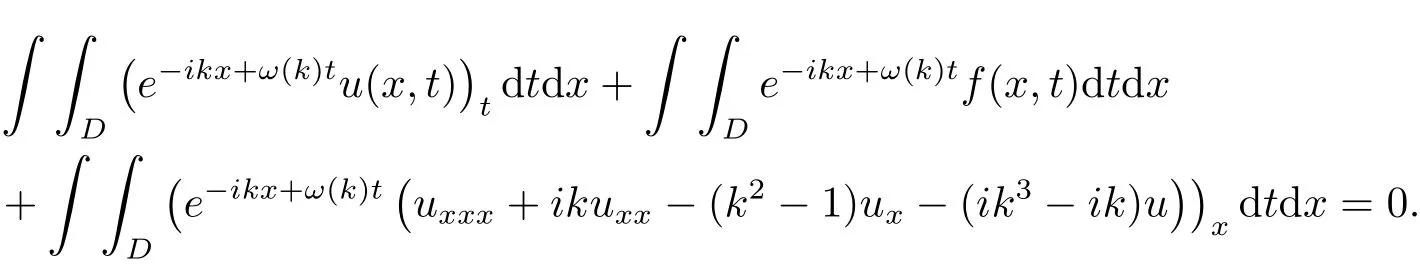
使用Green公式,有

即

定义在半直线上函数u(x,t)的Fourier变换为

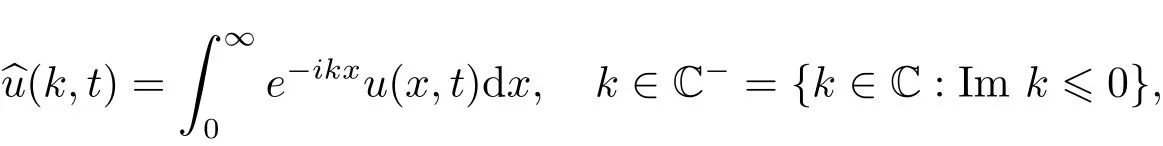
这里Re(−ikx)=xImk≤0.另外,记

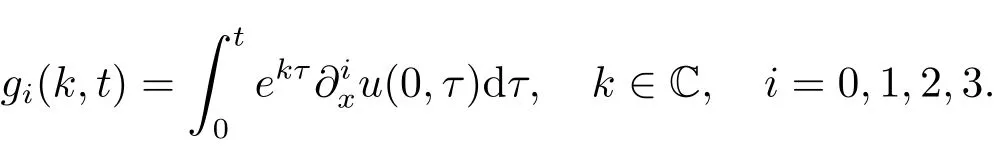
则下列整体关系等式成立

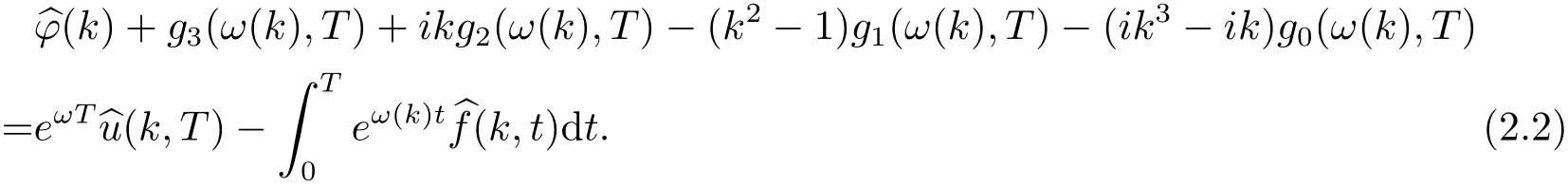
把上式中的T替换为t,并令

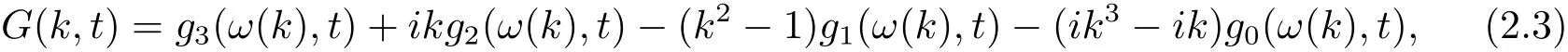
则有

定义区域

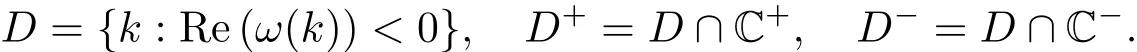
由于

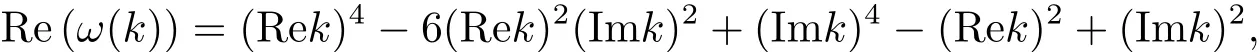
由Fourier逆变换公式,得到

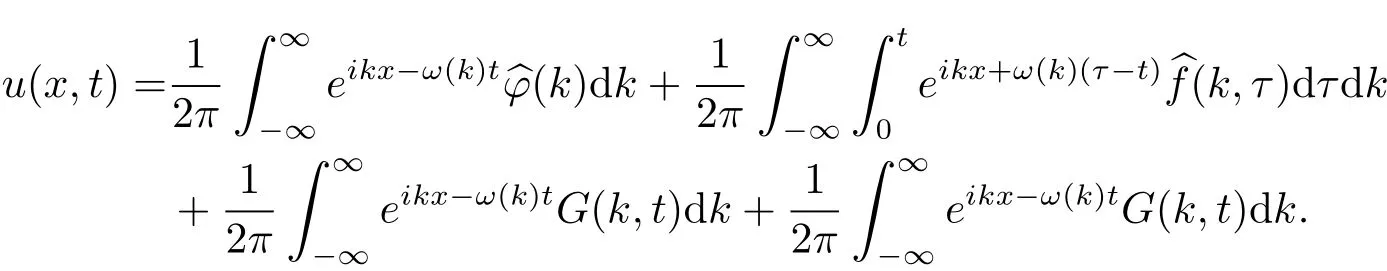
利用与Fokas[14]文中的第一章命题1.1证明类似的方法,可以证明

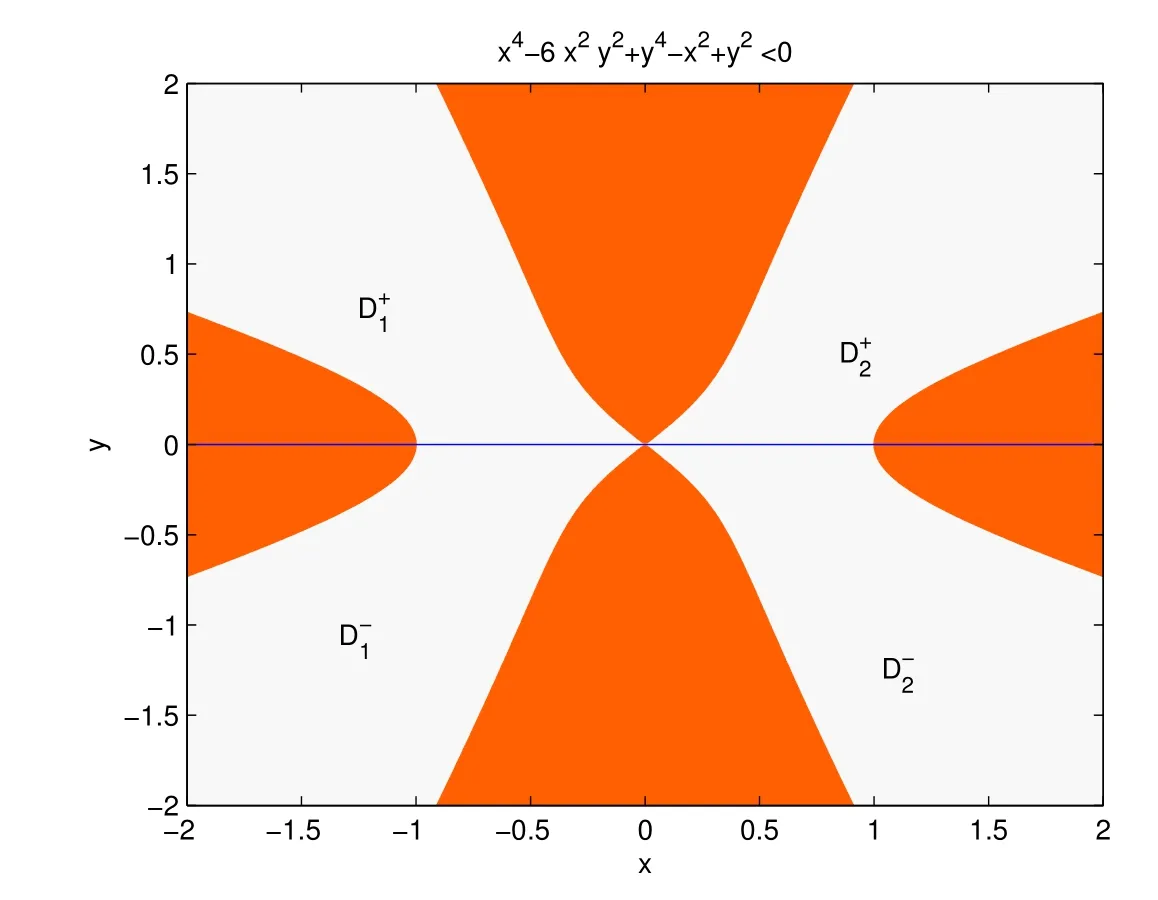
图1

在上式中,ϕ(x),f(x,t)是已知的,因此第一、二项直接可得.在后两项中,积分路径已知,被积函数G(k,t)中存在未知项g2,g3.下面用g0,g1来表示g2,g3.解方程k4−k2=µ4(k)−µ2(k),除µ(k)=k之外,还有三个根

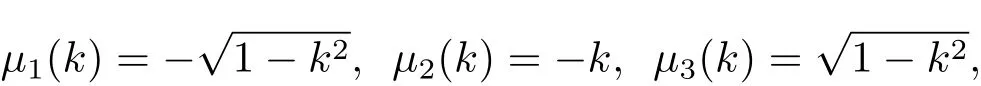
且满足

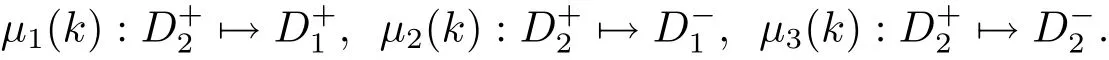
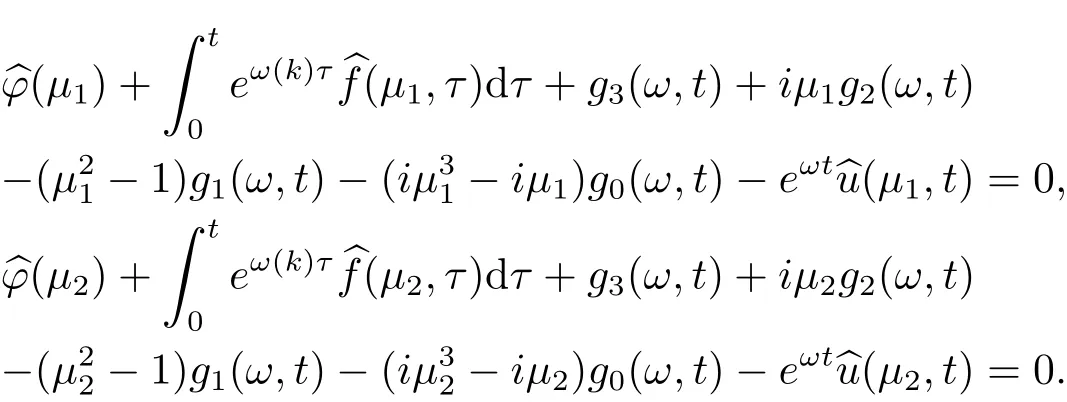
联立以上两式,解得

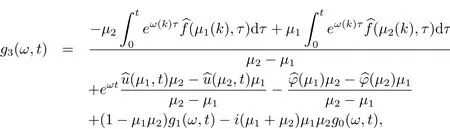
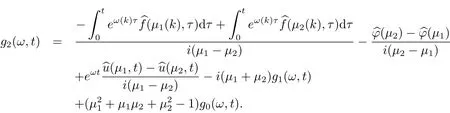
将g2(ω,t),g3(ω,t)代入(2.3)式,就可以计算(2.5)式的第三项

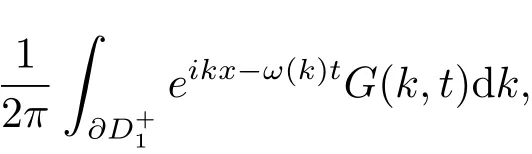
但其中有两部分包含未知函数u,即

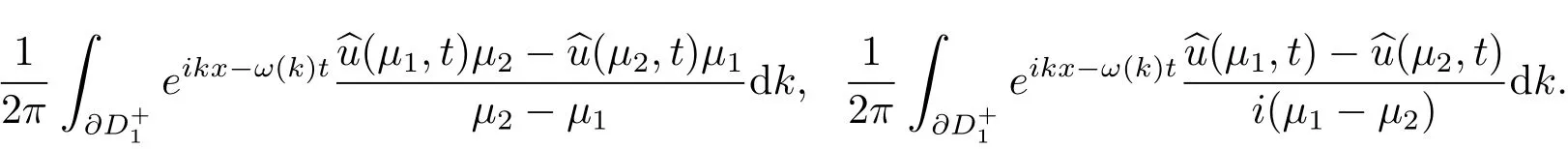
由于被积函数项在C+上是有界解析的,且当k→∞时,它们一致收敛到0,利用Jordan引理可知,上面两个积分均为0.令

则

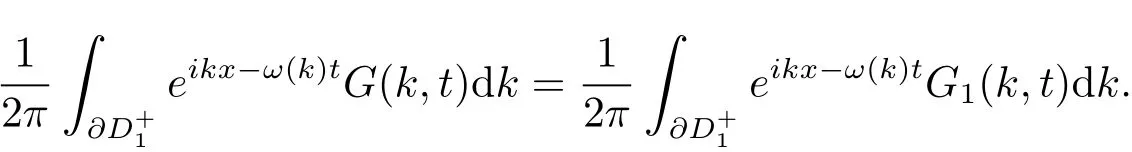
同理,令

则

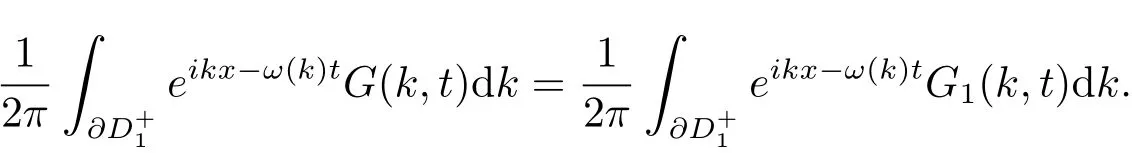
定理得到证明.