Fock型空间上的加权复合算子

赵 健,杨丛丽,潘维烨

(贵州师范大学数学科学学院,贵州贵阳 550001)

1 引言

设C表示复平面,H(C)表示在C上的解析函数全体,dA表示C上的Lebesgue面积测度,是由L2(C,e−α|z|2dA(z))中的整函数所构成的空间,0＜α＜∞,即

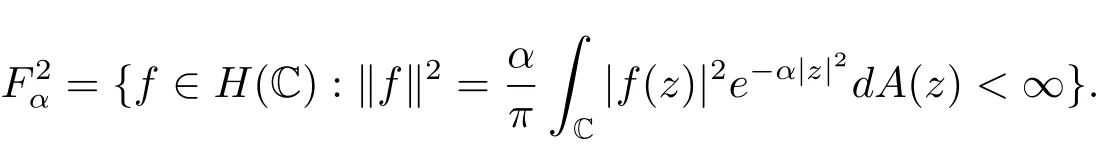
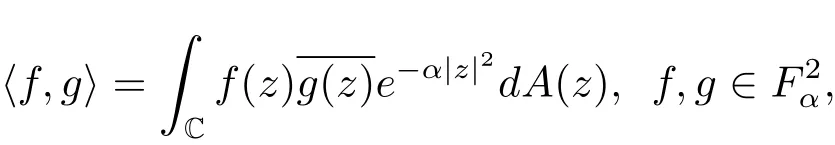
其规范正交系为

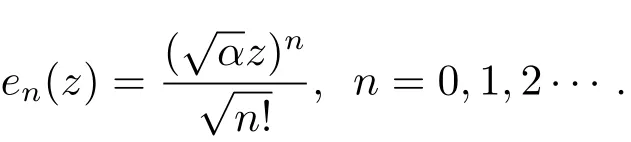
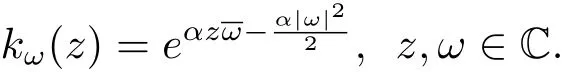
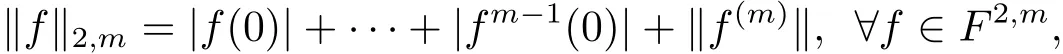
这里‖·‖表示F2的范数.

Cho和Zhu[8]证明了f∈F2,m当且仅当zmf∈F2.因此,F2,m的范数也可以表示为

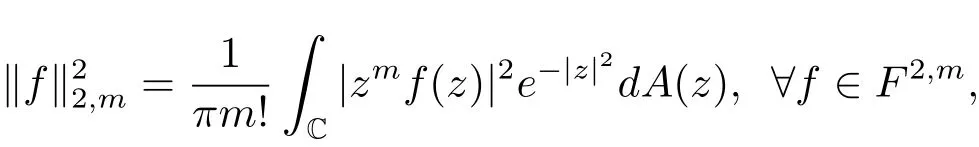
有关Fock-Sobolev空间的更多研究,可参见文献[9–14].

设T∈B(X),X 是Hilbert空间,称T是X上的Hilbert-Schmidt算子,如果

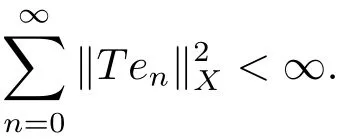
在本文中M表示一个正常数,每次出现不一定相同.

2 主要结果及证明

为了证明本文的主要结果,需要用到下面的一些辅助结论.

引理2.1设ϕ是C上的解析自映射,µ∈H(C),0＜α＜∞,则为紧的充分必要条件为有界且对中任意有界并在C的任意紧子集上一致收敛于0的序列{fn},n∈N+,有

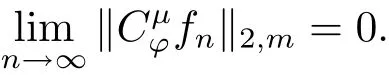
通过使用类似于文献[21,命题3.11]的方法,可以证明引理2.1.

引理2.2若序列{fn}在中弱收敛于0,则{fn}一致有界且在C的任意紧子集上一致收敛于0.

证由于序列{fn}在中弱收敛于0,则对任意于是

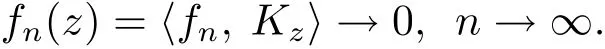
因此存在与z有关的常数Mz＞0,使得|fn(z)|≤Mz,而C是完备的,由一致有界原理可得序列{fn}一致有界,即存在M ＞0,使得设D是C中的任一紧子集,Kz为的再生核,可将Kz看成是C到上的一个映射,且对任意z0∈D,有

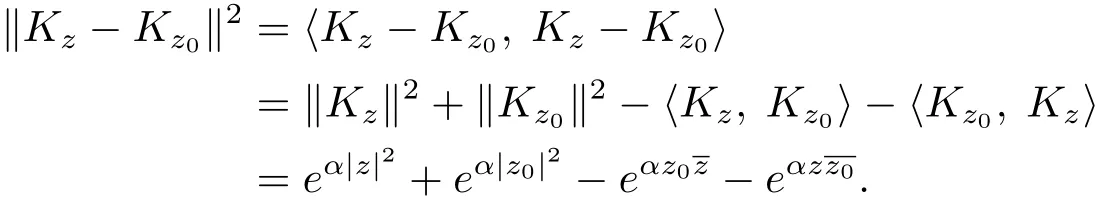
显然,当z→z0时,‖Kz−Kz0‖→0,这说明Kz为连续映射,由于D是紧的,故Kz在D上一致连续.因此对任意的ε＞0,存在δ＞0,对任意的z′,z′′∈D,当|z−z0|＜δ时,

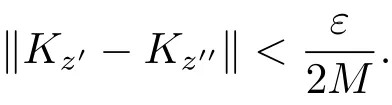
由于 D紧,则 D是完全有界的,于是,对上述的 δ,存在 z1,z2,···,zq∈ D,使得 D ⊂由于

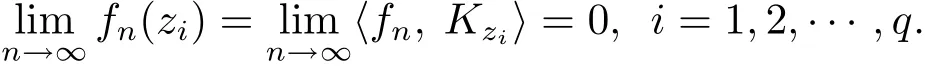
因此对上述的 ε,存在 Ni＞ 0,i=1,2,···,q,当任意 n ＞ Ni时,从而取N=max{N1,N2,···,Nq},对任意的z∈ D,一定存在zj∈ D,1≤ j≤ q,使得|z−zj|＜ δ,当任意的n＞N时,有

故{fn}在C的任一紧子集上一致收敛于0.

引理2.3设ϕ是C上的解析自映射,µ∈H(C),0＜α＜∞,则为紧的充分必要条件为有界且对中任意弱收敛于0的序列{fn},n∈N+,有

证 由引理2.1和引理2.2即可得证.

引理2.4设kω为中的正规化再生核,则当|ω|→∞时,kω弱收敛于0.即对任意的

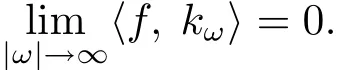
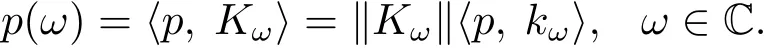
于是

下面的引理是文献[22,推论2.8]稍作推广后的结果,它在本文主要结果的证明中有着重要作用.当α=1时,就是文献[22]中的结论.

使用类似于文献[22]的方法可以证明引理2.5.

下面的结论来自于文献[23].

引理2.6设ϕ是C上的解析自映射,µ∈H(C),0＜α＜∞,若

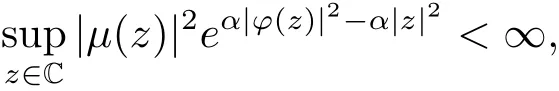
则存在常数a,b∈C且|a|≤1,使得ϕ(z)=az+b,z∈C.进一步,若

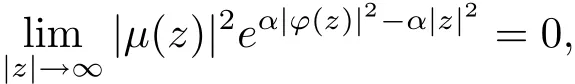
则ϕ(z)=az+b,z∈C且|a|＜1.

严格地说,引理2.6是文献[23]中结论稍作推广后的结果,当α=1时,引理2.6就是文献[23]中的结论.实际上,上述各个引理中的常数α在具体的证明中并没有本质作用.

接下来证明本文的主要结论.

定理2.1设ϕ是C上的解析自映射,µ∈H(C)且µ≠0,0＜α＜∞,则下列陈述等价:

(ii)

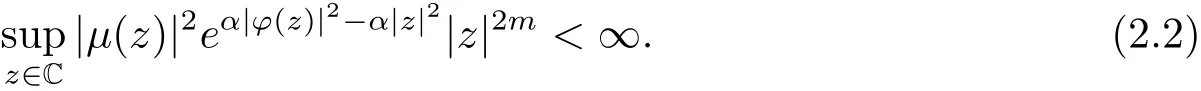
从而

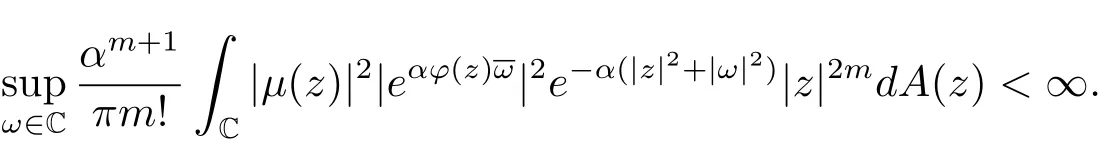
即(2.1)式成立.

(ii)⇒(iii).若(2.1)式成立,则对任意ω∈C,

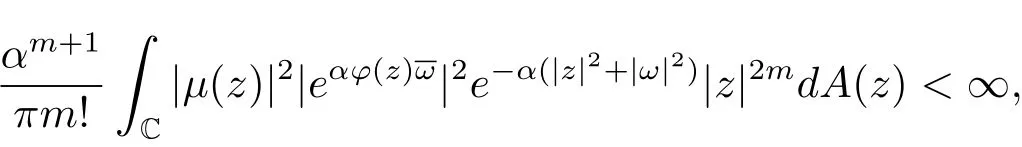
即

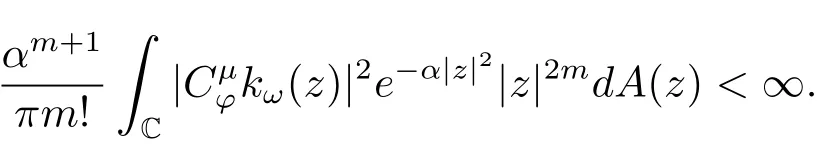
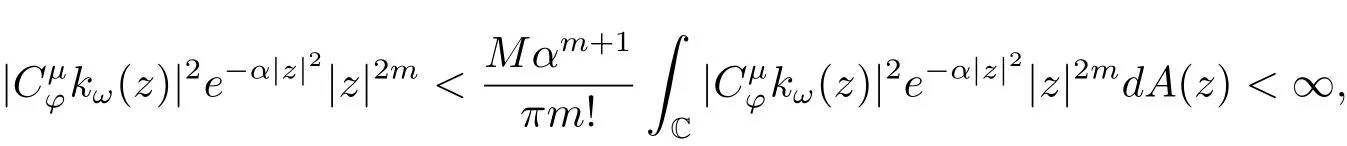
即

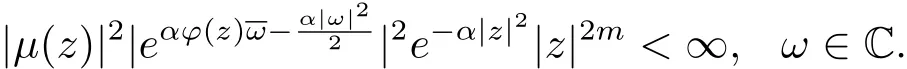
特别地,取ω=ϕ(z),则

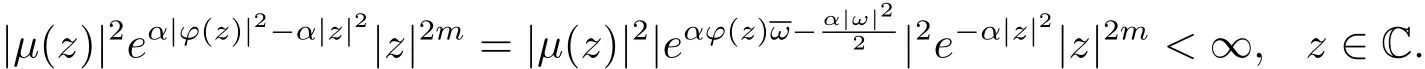
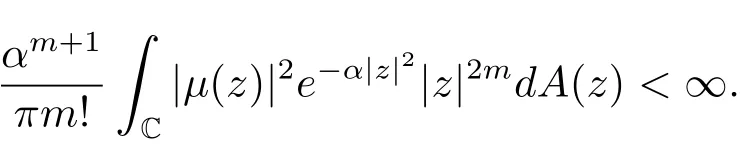
(iii)⇒(i).若存在常数a,b∈C,|a|≤ 1,使得ϕ(z)=az+b,z∈C.令ω= ϕ(z),则当0＜|a|≤1时,由(2.2)式,存在M ＞0,使得

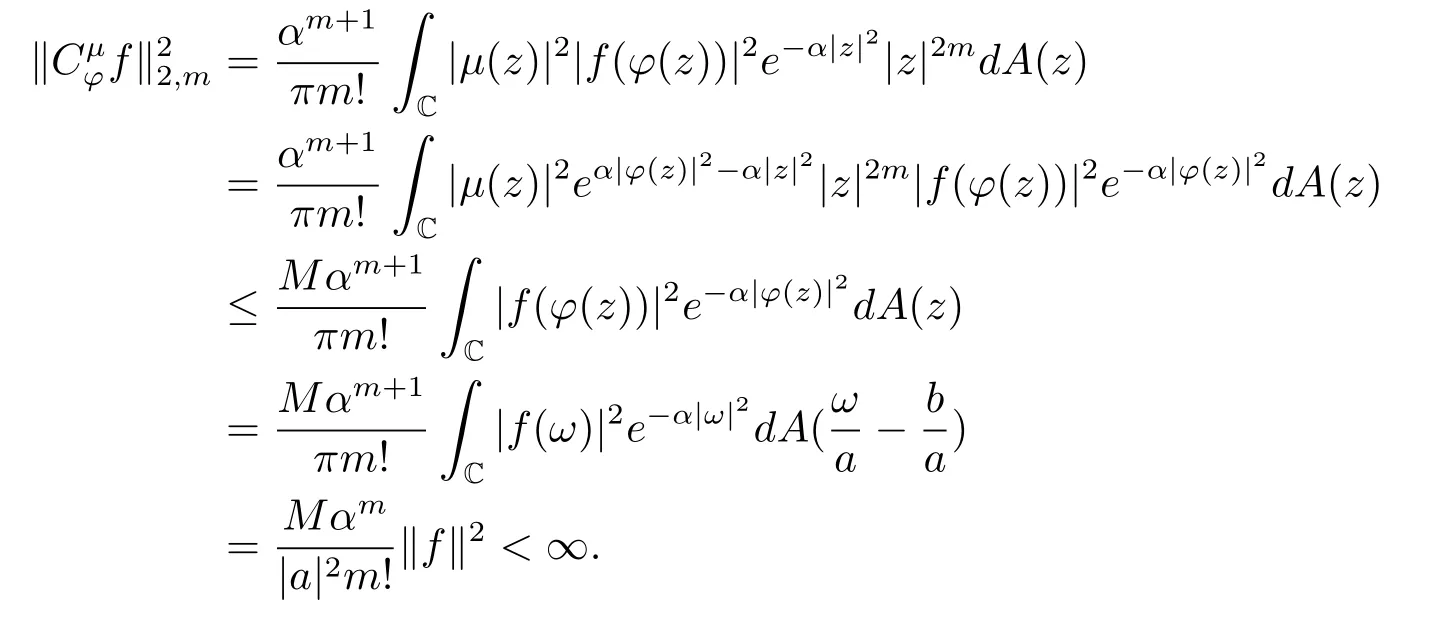
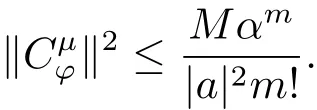
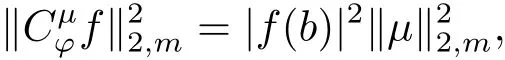
定理2.2设ϕ是C上的解析自映射,µ∈H(C)且µ≠0,0＜α＜∞,则下列陈述等价:

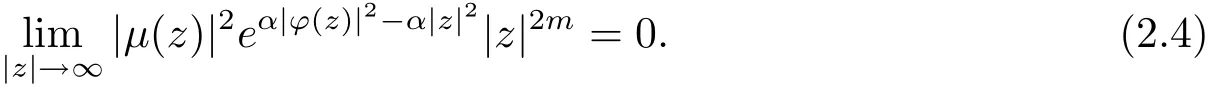
设kω为中的正规化再生核,{ωn}为C中任意趋于无穷的点列,由引理2.4,当n→∞时,{kωn}弱收敛于0.于是

从

而

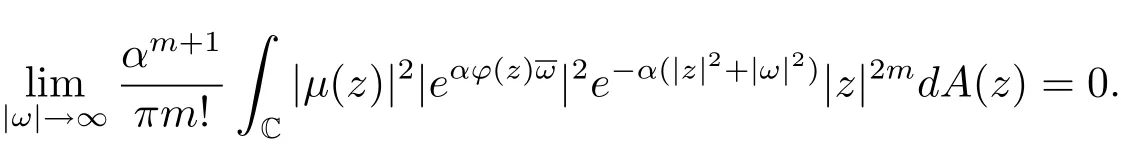
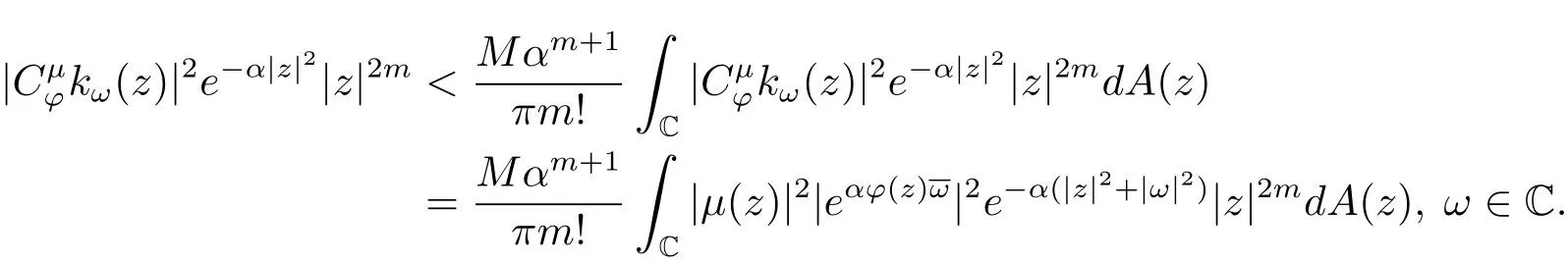
由(2.3)式可得

由上式,任意的ε＞0,存在Rε＞0,当|ω|＞Rε时,

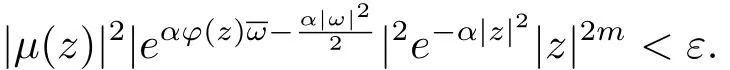
当0＜ |a|≤ 1时,令 ω = ϕ(z),则 |ω|=|ϕ(z)|→ ∞,|z|→ ∞,因此,对上述的Rε,存在R′＞ 0,当 |z|＞ R′时,有 |ω|=|ϕ(z)|＞ Rε.于是对上述的 ε,取 R=R′,当 |z|＞ R 时,|ω|=|ϕ(z)|＞ Rε且

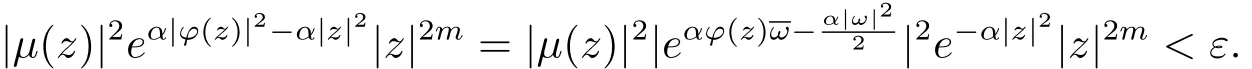
当|a|=0时,ϕ(z)=b,由上述情形易知,这时(2.4)式仍然成立.

由(2.4)式容易得到

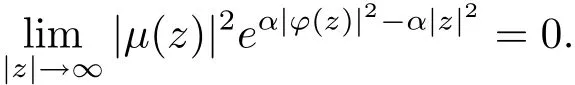
再由引理2.6知|a|＜1.

(iii)⇒(i).设{fn}为中任意有界且在C的任一紧子集上一致收敛于0的序列,则存在C1＞0,使得‖fn‖≤C1.由于µ∈,则存在C2＞0,使得‖µ‖2,m≤C2.若存在常数a,b∈C,|a|＜1,使得ϕ(z)=az+b,z∈C.令ω=ϕ(z),当0＜|a|＜1时,

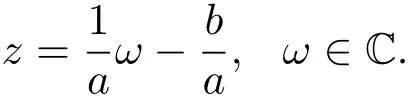
由(2.4)式,对任意的ε＞0,存在R＞0,当|z|＞R时,

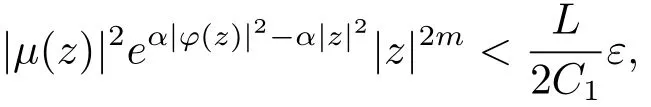
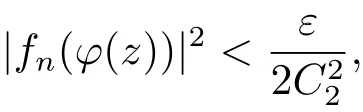
那么取N=Nε,当n＞N 时,有

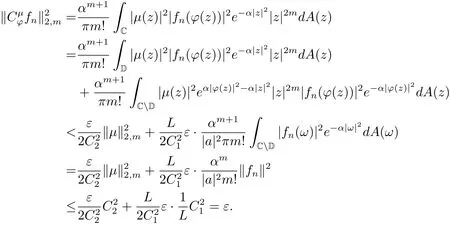
当|a|=0时,ϕ(z)=b,此时有

接下来讨论Hilbert空间上的一类重要算子–Hilbert-Schmidt算子.文献[8]给出了Fock空间F2上的加权复合算子是Hilbert-Schmidt算子的完全刻画,其证明过程可以平行地推广到Cn上的Fock空间.下面给出空间上的加权复合算子是Hilbert-Schmidt算子的一个充分必要条件.

定理2.3设ϕ是C上的解析自映射,µ∈H(C),0＜α＜∞,若有界,则是上的Hilbert-Schmidt算子的充分必要条件为

证设(2.5)式成立,记en为的规范正交系,则

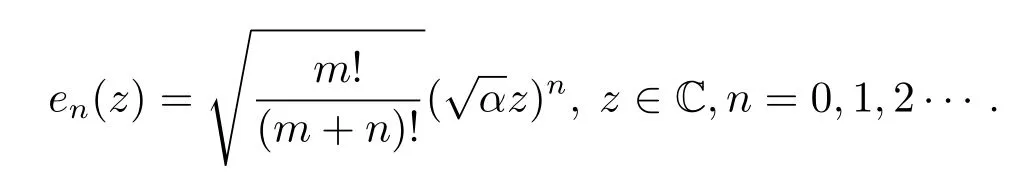
从而

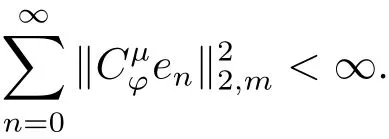
由上述证明过程有

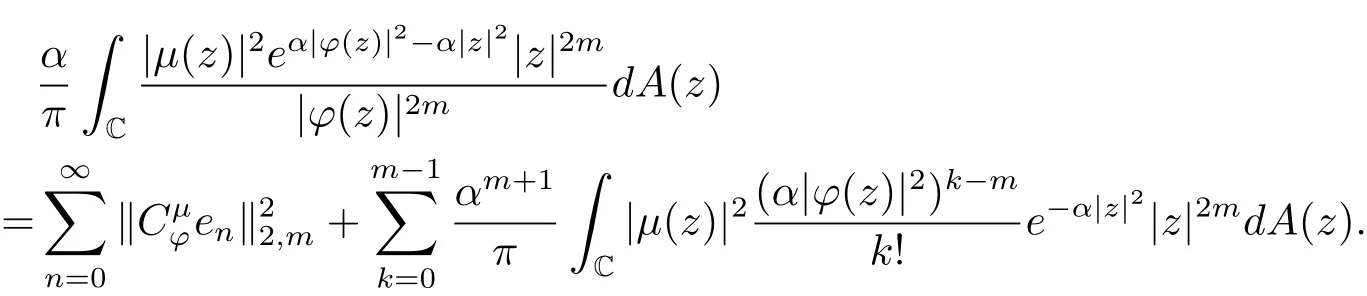
显然,要得到(2.5)式,只需上式等号右边第二项有界即可.为此,令

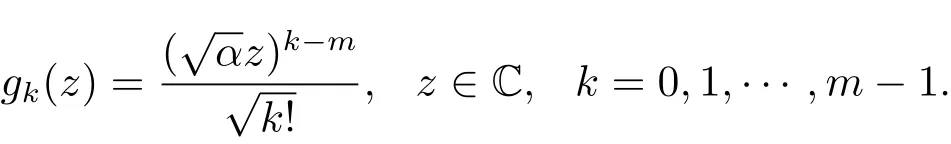
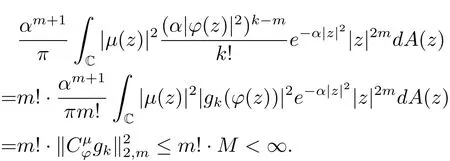
进而有

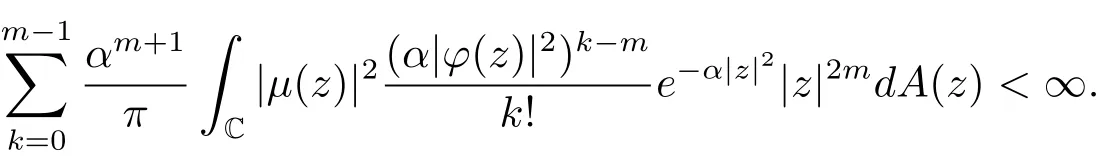
故(2.5)式成立.