紧扣图形特征 揭示问题本源

王 松

（湖北省武汉市武汉第三寄宿中学）

笔者在研读近几年有关中考命题、解题类文章时，发现很多有关“共顶点三角形旋转”模型的文章，一直困惑于此模型的辅助线是如何产生的？本文以一道几何题为线索，从图形位似的角度，谈谈自己对此类问题的理解.

题目如图1，在等腰直角三角形ABC中，AC=，点P在以斜边AB为直径的半圆上，M为PC的中点．当点P沿半圆从点A运动至点B时，点M运动的路径长是（ ）.

（B）π

（D）2

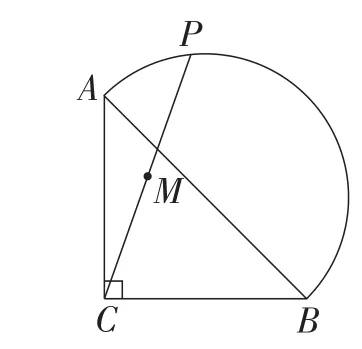
图1

一、问题起源

人教版《义务教育教科书·数学》九年级下册第27章第3节“位似”中给出了位似的概念.依据题目给出的条件不难判断动点P和动点M的连线都经过同一点C，且，故可以判定点P的运动轨迹与点M的运动轨迹是以点C为位似中心，位似比为2∶1的位似图形.进而可知点M的运动轨迹是以1为半径的半圆，其路径长为π.

显然，对于平面内一定点O和动点P，连接OP，在线段OP上取一点Q，始终满足（k为定值）.如果规定动点P在一条确定直线l上运动时（如图2），依据位似的定义可知，点Q的运动轨迹必为一条与直线l平行的直线.进而，若点P的运动轨迹为直线l上某一线段PP1时，点Q的运动轨迹必为一条平行于线段PP1的线段QQ1，且有QQ1=k·PP1.如果规定动点P在一确定⊙R上运动时（如图3），依据位似的定义可知，点Q的运动轨迹必为一个圆（其圆心R1与点R，O三点共线），且有C⊙R1=k·C⊙R.

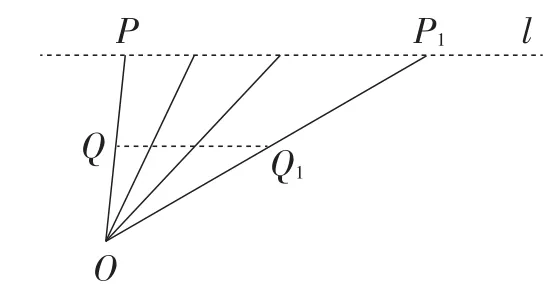
图2

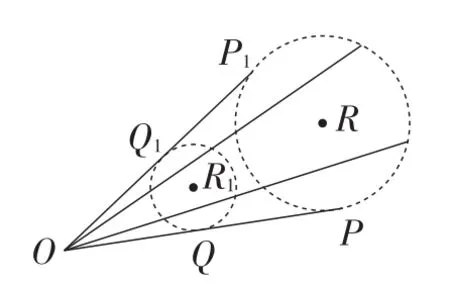
图3

当然，动点P的运动轨迹可以定义为任意轨迹，动点Q的运动轨迹将始终保证与动点P的运动轨迹关于定点O成位似图形，由于情况多样而本质不变，故不再赘述.

二、问题变式

变式：对于图2中的问题，若将点Q绕着点O顺时针旋转α(0＜α＜360°)，且α≠180°，其他条件不变.

（1）如果规定动点P在一条确定直线l上运动时（如图4），依据前面的论述，点Q的运动轨迹必为一条与直线l相交的直线，其夹角之一为α.

理由如下：在图4中，直线PP1与直线QQ1交于点T，由于，∠POQ=∠P1OQ1=α，易证得△POQ∽△P1OQ1，△POP1∽△QOQ1.故∠TPO=∠TQO.证得∠T=∠POQ=α.进而，若点P的运动轨迹为直线l上某一线段PP1时，点Q的运动轨迹必为一条线段QQ1，此时QQ1=k·PP1.同时还可以发现其本质为图2中△QOQ1整体绕点O顺时针旋转α后即为图4中的△QOQ1.

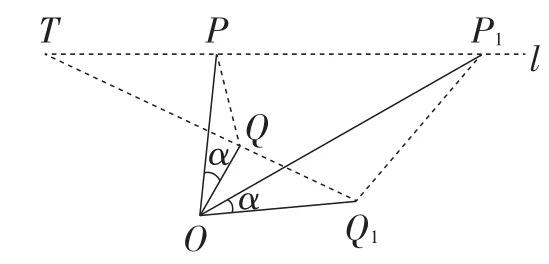
图4

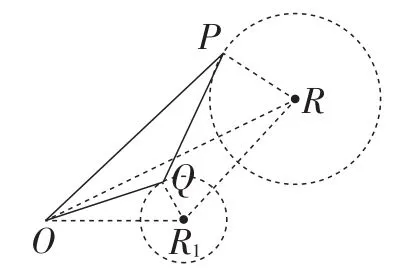
图5

（2）如果规定动点P在一确定⊙R上运动时（如图5），依据前面的论述，点Q的运动轨迹可以看作是图3中的⊙R1绕点O顺时针旋转α后得到的一个圆，且有C⊙R1=k·C⊙R.理由如下：如图5，连接OR，作∠ROR1=α，并使得，易证△POQ∽△ROR1，△POR∽△QOR1.得.故可以得到点Q在以R1为圆心，k·PR为半径的圆上运动，故

显然，当动点P的运动轨迹为⊙R上的一段弧时，动点Q的运动轨迹也应为一段弧，同时两段弧所对的圆心角相等，弧长之比等于k.

在上述证明过程中，证得△POQ∽△ROR1.同时观察发现点O为这对相似三角形的公共顶点，P，Q这对对应点同为运动过程中的动点，R，R1这对对应点同为圆心，此规律也为我们解决相关问题提供了依据.

例1如图6，在△ABC中，∠ACB=90°，CA=CB=4，CD⊥AB于点D，P是CD上一个动点，以点P为直角顶点向下作等腰直角三角形PBE，连接DE，求DE的最小值．

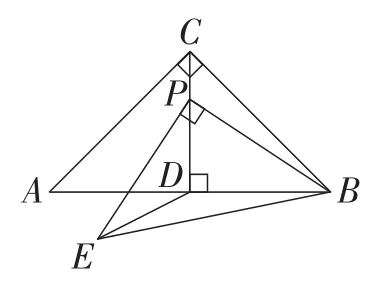
图6

分析：由已知可得△ABC∽△EPB.进而可得△BCP∽△BAE.动点P在定线段CD上运动，则点P的对应点E必在某定线段上运动，故拟定思路如下：由△BCP与△BAE始终相似确定点E所在线段，再寻找定点D到定线段的最小距离.

解：如图7，以DB为直角边在AB下方构造等腰直角三角形BDF，

当点P运动到与点C重合时，点E与点A重合；

当点P运动到与点D重合时，点E与点F重合，

所以点E在线段AF上运动.

过点D作DG⊥AF于点G，

图7

当点E运动到点G的位置时，DE有最小值.

因为AC=BC=4，

所以DB=AD=DF=

所以DG=2.

例2如图8，AB是⊙O的直径，点C在AB的延长线上，AB=BC=10，P是⊙O上一动点，连接PC，以PC为边作△PCD，使∠PDC=90°，，P，C，D三点为逆时针顺序.连接OD，则线段OD长的最小值是_____．

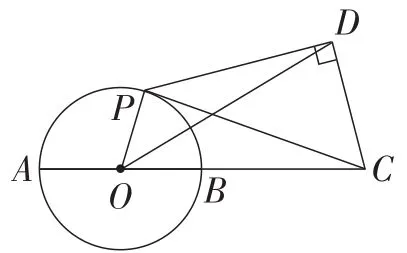
图8

分析：由已知可知，点P始终在定⊙O上运动，（即∠DCP为确定角），可以猜想到点D一定在某一定圆上运动，故找到这个定⊙I（如图9），连接OI，当点D运动到线段OI上即可找到线段OD的最小值.

解：如图9，以OC为斜边构造Rt△OCI，

因为∠DPC=∠IOC，

∠PDC=∠OIC，

所以△PDC∽△OIC.

图9

所以△DCI∽△PCO.

又因为AB=BC=10，

所以OC=15.

可求得OI=12.

所以ID=3.

因为点I是定点，ID是定长，

所以点D在半径为3的⊙I上运动.

所以OD的最小值为12-3=9.

显然，由于已经确定了动点D的运动轨迹为以定点I为圆心，半径为3的一个圆，当然亦可求线段OD的最大值和线段OD长度的取值范围，在此就不展开说明了.

三、问题拓展

在前面问题起源中，我们谈到从位似的角度来理解以上问题，而从两种位似情形来看，不难猜想到当位似中心在对应点连线上时，上述结论也是成立的.

拓展1：对于平面内一定点O和一动点P，连接OP，在线段PO的延长线上取一点Q，始终满足（k为定值）.

（1）如果规定动点P在一条确定直线l上运动时（如图10），依据位似的定义可知，点Q的运动轨迹必为一条与直线l平行的直线.进而，若点P的运动轨迹为直线l上某一线段PP1时，点Q的运动轨迹必为一条平行于线段PP1的位似线段QQ1，且有QQ1=k·PP1.

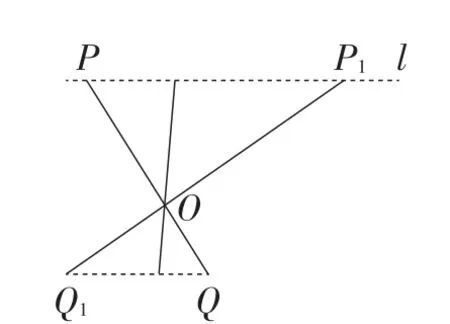
图10

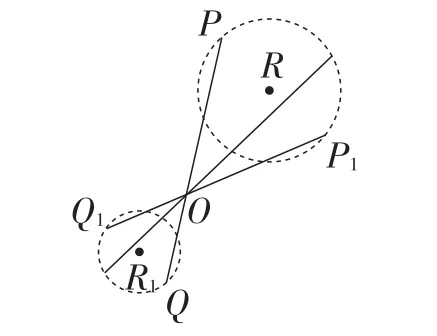
图11

（2）如果规定动点P在一确定⊙R上运动时（如图11），依据位似的定义可知，点Q的运动轨迹必为一个圆（其圆心R1与点R，O三点共线），且有

当然，动点P的运动轨迹可以定义为任意轨迹，动点Q的运动轨迹将始终保证与动点P的运动轨迹关于定点O成位似图形，由于情况多样而本质不变，故不再赘述.

拓展2：对于平面内一定点O和一动点P，连接OP，在平面内再取一点Q，连接OQ，始终满足（k为定值），且∠POQ=α(0＜α＜360°，且α≠180°).

（1）如果规定动点P在一条确定直线l上运动时（如图12），依据前面的论述，我们可以认为是图10中的△QOQ1整体绕点O逆时针旋转180°-α后得到的，点Q的运动轨迹必为一条与直线l相交的直线，其夹角之一为α.

图12

理由如下：在图12中，直线PP1与QQ1交于点T，由于，∠POQ=∠P1OQ1=α，

易证得△POQ∽△P1OQ1，POP1∽△QOQ1.

进而可以证得∠PP1O=∠QQ1O.

得∠T=180°-α.

（2）如果规定动点P在一确定⊙R上运动时（如图13），依据前面的论述，点Q的运动轨迹可以认为是图11中的⊙R1绕点O逆时针旋转180°-α后得到的一个圆，且有C⊙R1=k·C⊙R.

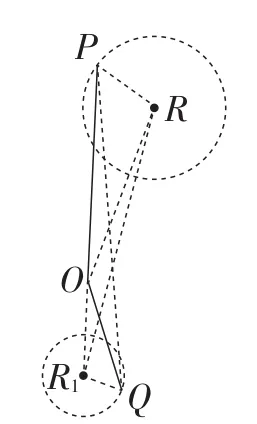
图13

理由如下：如图13，连接OR，作∠ROR1=α，并使得，易证△POQ∽ △ROR1，POR∽ △QOR1，得.故可以得到点Q在以R1为圆心，k·PR为半径的圆上运动，故C⊙R1=k·C⊙R.

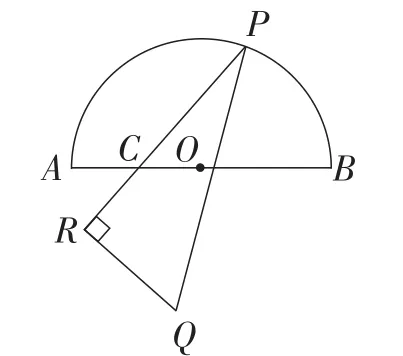
图14

例3如图14，点P为半圆O上一动点，直径AB=16，C为OA中点，过点C的线段PR始终满足PC=2CR，以PR为直角边作 Rt△PRQ，∠R=90°，PR=2RQ，则BQ的最小值为______.

分析：如图15，连接CQ，可发现RC∶RQ∶CP=2∶3∶4，可得CQ∶PC=13 ∶4，.故可以判断当动点P在半圆O上运动时，动点Q必在某一半圆上运动，进而通过确定这个圆的两个要素（圆心、半径），最终发现BQ的最小值.

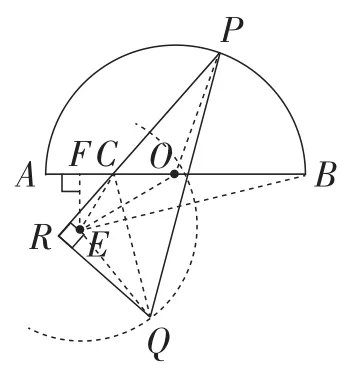
图15

解：如图15，连接CQ，

因为RC∶RQ∶CP=2∶3∶4，

所以CQ∶PC=∶4，

tan∠RCQ=.

在AB下方取点E，连接CE，

使得∠ACE=∠RCQ，CE∶OC=∶4，

易证△CPQ∽△COE，△CEQ∽△COP.

过点E作EF⊥AB于点F，连接EB，由OC=4，

可得CF=2，EF=3.

在Rt△BEF中，FB=14，EF=3，

所以BQ的最小值为E，B，Q三点共线时，其值为

通过以上举例，笔者发现利用“共顶点三角形旋转”模型来解决相关问题时，所添加的辅助线并非凭空捏造，而是有章可循的，之所以对这类构造方法感到无从下手，恰恰是忽视了问题的本源——位似图形，若能从根源上揭示问题本质，进而可以寻求到通解、通法来解决问题.