关注核心素养 引领课堂教学——2017年海南省中考试卷第24题解法赏析及教学启示

孙孝武，吴永德，房一登

（海南省教育研究培训院；北京师范大学万宁附属中学；海南省海南中学）

2017年海南省中考试卷第24题，沿袭了历年来海南省中考数学压轴题的特色.此题以二次函数为载体，充分地综合了代数与几何的知识，很好地渗透了数学思想方法，特别是数形结合思想.此题涉及到的数学思想方法主要有：待定系数法，函数与方程思想，数形结合思想，分类讨论思想，等等.此题题干表述简炼，解题思路清晰，要求学生具有较强的分析问题和解决问题的能力.作为压轴题，此题具有较好的效度、信度、区分度，实际阅卷后的数据分析也体现了这些特点.

一、试题呈现

题目抛物线y=ax2+bx+3经过点A(1，0)和点B(5，0).

（1）求该抛物线所对应的函数解析式.

①如图1（1），连接PC，PD，在点P运动过程中，△PCD的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由.

②如图1（2），连接PB，过点C作CQ⊥PM，垂足为点Q，是否存在点P，使得△CNQ与△PBM相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由.

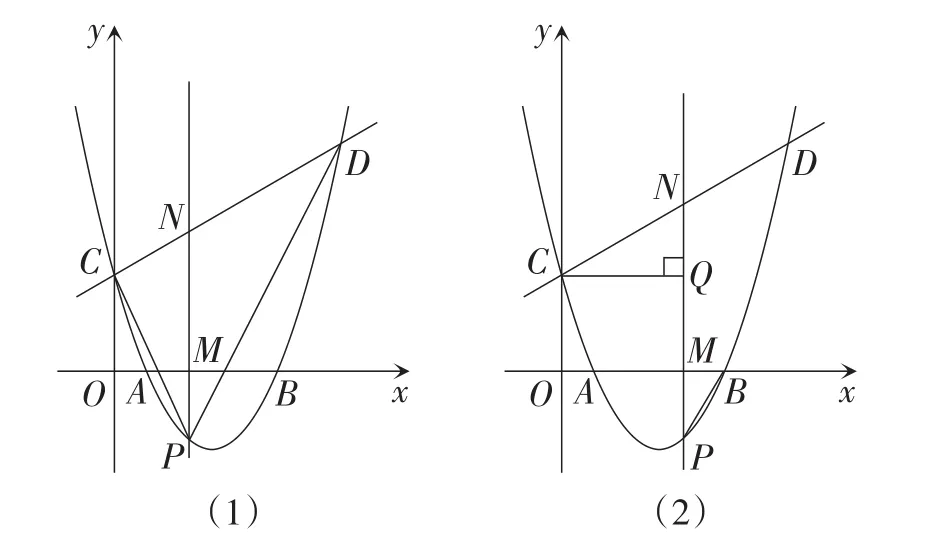
图1

二、命题设想

第（1）小题求函数的解析式是基础题，也是函数的重点内容，这是问题设计由易到难的需要.二次函数解析式有三种形式，即一般式，顶点式，交点式.此题给出了抛物线与x轴的两个交点坐标，如果运用交点式，设y=a(x-1)(x-5)，只有a待定，相比于运用其他两种形式而言，这个方法比较容易，也能有效地避免差错出现.如果第（1）小题出了差错，即使第（2）小题解答的思路清晰、表达完美、字迹工整，但得分不高.因为后续题目的解答都是建立在第（1）小题的基础上，所以选择适当的方法解决问题很重要.

第（2）小题分为两问，这两问的图形具有较高的关联度，但考查的知识点不同.第①问重点考查在平面直角坐标系中求图形面积的最大值，其中用割补法表示面积的思路更加普遍，解决过程中需要用字母表示变量，构造出二次函数模型，从而求最大值；第②问涉及相似三角形的知识，可以从相似三角形的不同判定方法考虑，从而衍生出不同的解法.

三、解法赏析

1.第（1）小题思路和解法赏析

思路1：利用一般式求解.

解法1：因为抛物线y=ax2+bx+3经过点A(1 ，0)和点B(5，0 )，

思路2：利用交点式求解.

解法2：因为抛物线经过点A(1，0)和B(5，0)，

所以抛物线解析式可设为y=a(x-1)(x-5).

由抛物线解析式y=ax2+bx+3可知，抛物线经过点C(0，3).

所以3=a(0-1)(0-5).

思路3：利用顶点式求解.

解法3：因为抛物线经过点A(1 ，0)和B(5，0)，

设抛物线的解析式为y=a(x-3)2+k.

将点A(1 ，0)和点C(0，3)代入y=a(x-3)2+k，

2.第（2）小题第①问思路和解法赏析

首先，求出C，D两点坐标，

所以点C，D的坐标分别为

思路1：利用割补法表示面积，再求最大值.

解法1：由已知可设点由于点P在x轴下方，可知1＜t＜5.

因为直线PM∥Oy，分别与x轴和直线CD相交于点M，N，

所以点M，N的坐标分别为

如图2，分别过点C和点D作直线PN的垂线，垂足分别为点E，F，

则CE=t，DF=7-t.

所以当PN最大时，△PCD的面积最大.

此时，△PCD的面积最大，最大值为

图2

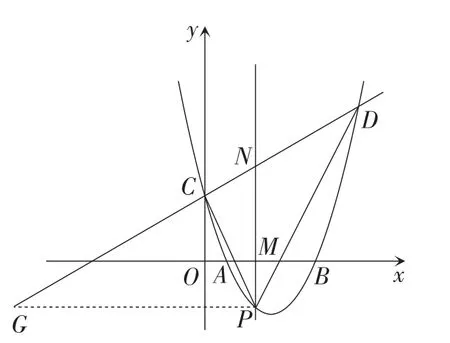
图3

解法2：如图3，过点P作PG∥Ox，PG交直线DC于点G，

此时，S△PCD=S△PDG-S△PCG.

本方法解题过程类似于解法1，此处不再赘述.

解法3：如图4，过点P作PE⊥Oy，垂足为点E，过点D作DF⊥EP，交EP的延长线于点F，

此时，S△PCD=S梯形CEFD-S△PCE-S△PDF.

本方法解题过程类似于解法1，此处不再赘述.

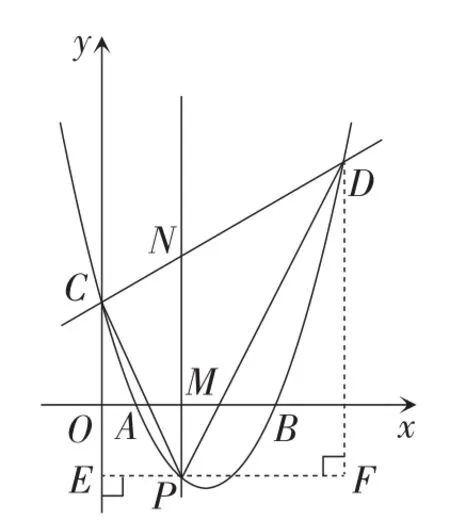
图4

图5

解法4：如图5，过点P作PE⊥Oy，垂足为点E，连接DE，

此时S△PCD=S△CED+S△EPD-S△PCE.

本方法解题过程类似于解法1，此处不再赘述.

思路2：利用平行线求最大值.

解法5：如图6，过点P作直线l∥CD，则可设直线l的解析式为

图6

当直线l与抛物线相切时，△PCD的面积最大.

所以此时点P的坐标为

此时，点N的坐标为

此时△PCD的面积最大，

思路3：利用“化斜为直”，直接表示三角形的底和高求最大值.

解法6：如图7，由已知，可以设点P的坐标为，由点P在x轴下方，可知1＜t＜5.

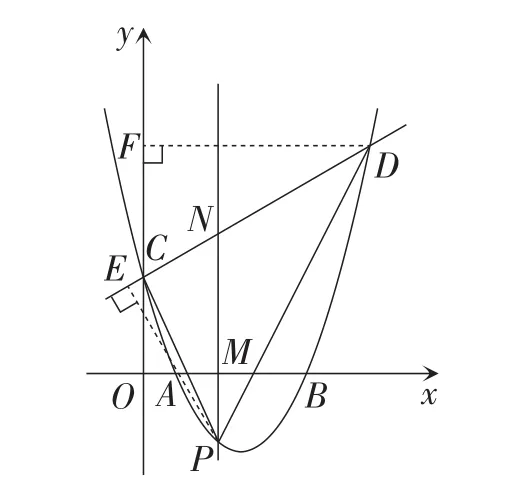
图7

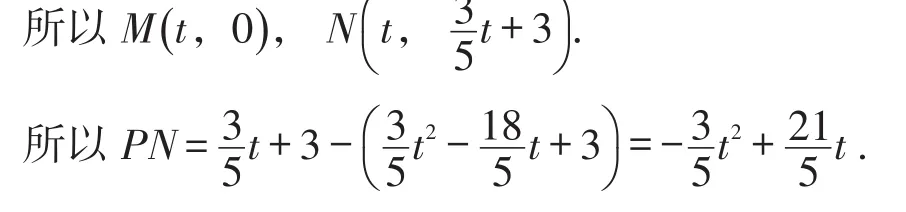
过点P作PE⊥CD于点E，过点D作DF⊥Oy于点F，

则∠PEN=∠DFC=90°.

又由PM∥Oy，得∠PNE=∠DCF.

故Rt△PNE∽ Rt△DCF. 得

3.第（2）小题第②问解法赏析

解法1：如图1（2），因为 ∠CQN=∠PMB=90°，

得△CNQ∽△PBM.

设Q(t，3)，则.

此时点P的坐标为.

此时点P的坐标.

解法2：如图1（2），因为∠CQN=∠PMB=90°，

所以当∠NCQ=∠PBM或者∠NCQ=∠BPM时，

得△CNQ∽△PBM.

情况1：当∠NCQ=∠PBM时，

tan∠NCQ=tan∠PBM，即

此时可转化为解法1中的情况1，此处不再赘述.

情况2：当∠NCQ=∠BPM时，

tan∠NCQ=tan∠BPM，即

此时可转化为解法1中的情况2，此处不再赘述.

使得△CNQ∽△PBM.

四、教学启示

从以上的题目分析和解题赏析过程中，我们得到以下启示.

1.教学过程中应以《义务教育数学课程标准（2011年版）》为标准，以教材为根本，关注学生

中考试题的命制是以《义务教育数课程标准（2011年版）》（以下简称《标准》）为标准，以教材为根本，根据九年级学生的生理特点、心理特点等来命制，很多题目的情境或原型都来自教材.题目的第（1）小题和第（2）小题第②问都来源于教材.一般来说，我们的教学要关注基础知识的落实、解题经验的积累、应考能力的形成.这必然要求我们要关注《标准》，回归教材，关注学生.

2.教学过程中注意引导学生感悟数学思想，积累活动经验

在教学中，学生是学习的主体.教之道在于度，学之道在于悟.数学教学的最主要任务是引领学生学会思考，培养学生的思维能力，从学会思考走向学会学习.《标准》指出，数学思想蕴涵在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括，如抽象、分类、归纳、演绎、模型等.学生在积极参与教学活动的过程中，通过独立思考、合作交流，逐步感悟数学思想.此题的解决过程中体现了多种数学思想，需要学生具备一定的解题经验.

3.教学过程中关注核心素养，促进持续发展

《普通高中数学课程标准（2017年版）》提出，要引导学生会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界；同时要关注数学的六大核心素养：数学抽象，逻辑推理，数学建模，直观想象，数学运算，数据分析.此题作为压轴题，既重视推理，又重视直观想象，当然也不乏数学运算.所以在平时的教学中，教师要不断地引导学生通过实践、思考、探索、交流等，获得数学的基础知识、基本技能、基本思想、基本活动经验，促使学生主动地、富有个性的学习，不断提高发现问题和提出问题的能力、分析问题和解决问题的能力.

4.教学过程中注重信息技术，紧跟时代步伐

现代信息技术的广泛应用正在对数学课程内容、数学课堂教学、数学学习方式等方面产生深刻影响.信息技术工具的使用能为学生的数学学习和发展提供丰富多彩的教育环境和有力的学习工具.数学课程的设计与实施应根据实际情况合理地运用现代信息技术，要注意信息技术与课程内容的整合，注重实效；要充分考虑信息技术对数学学习内容和方式的影响，开发并向学生提供丰富的学习资源，把现代信息技术作为学生学习数学和解决问题的有力工具，有效地改进教与学的方式，使学生愿意并有可能投入到现实的、探索性的教学活动中去.例如，几何画板软件的运用，这个软件在数学教材的阅读材料中多次提及.像本文所述的这类压轴题，教师在备考时若利用几何画板软件进行讲解和变式，既能有效地帮助学生突破难点，又能更直观地理解数学问题的本质.

教学有法，教无定法，千题万题不如讲透一题，千法万法不如落实得法.教师在教学中，要吃透《标准》，以教材为本，以学生为本，引导学生夯实基础知识、强化基本技能、渗透基本数学思想、积累基本活动经验；加强对学生的学法指导，注意平时各类考试命题的针对性、层次性、导向性、侧重点、关键点；注重信息技术的运用，为学生提供有效的、鲜活的教学素材和资源.通过学习、反思、总结，内化为学生自己的知识与能力，形成学生自己的数学知识体系.