对一道中考压轴题的探究及推广

梁文威

（广东省江门市新会区会城源清中学）

2017年广东省中考数学压轴题考查了在平面直角坐标系背景下，已知矩形对角线上动点生成的平面几何问题与二次函数最值问题，既考查了学生的空间想象能力，又考查了分类讨论和函数思想，比较全面地考查了学生的数学核心素养，体现了中考数学压轴题考能力、考创新、考发展的要求，对今后一段时间的广东省初中数学教学起着重要的导向作用.笔者就2017年广东省中考数学压轴题进行探究与分析，并对相关结论进行拓展与推广.

一、试题呈现

题目如图1，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A(0，2 )和，点D是对角线AC上一动点（不与点A，C重合），连接BD，作DE⊥DB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF.

（1）填空：点B的坐标为_____.

（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，求出AD的长度；若不存在，说明理由.

②设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用①的结论），并求出y的最小值.

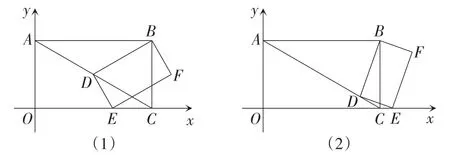
图1

二、解法探究

1.第（1）（2）小题的解法探究

第（1）小题考查了平面直角坐标系的基本概念，点B的坐标为.

第（2）小题中求使△DEC是等腰三角形时，线段AD的长.题目中隐藏了一个重要条件∠ACO=30°，而且还要考虑图1（1）和图1（2）的两种情况.第一种情况：如图1（1），由ED=EC，不难得到△BCD是等边三角形，进而可得∠DAB=∠DBA=30°.所以AD=BD=2.第二种情况：如图1（2），由CD=CE，易知∠CDE=15°，∠ADB=75°.进而可得∠ADB=∠ABD=75°.所以

解：（1）点B的坐标为

（2）存在；理由如下：

因为四边形ABCO是矩形，

所以 ∠ACO=30°.

情况1：如图1（1），当点E在点C左侧时，

因为△DEC是等腰三角形，即ED=EC，

所以∠ACO=∠EDC=30°.

因为DE⊥DB，所以∠BDC=60°.

又因为∠BCA=60°，即△BCD是等边三角形，

所以BD=BC=2.

因为AB∥OC，所以∠ACO=∠DAB=30°.

又因为∠ABD=∠BDC-∠DAB=30°，

即∠ABD=∠DAB，所以AD=BD=2.

情况2：如图1（2），当点E在点C右侧时，

因为△DEC是等腰三角形，即CD=CE，

所以∠CDE=∠CED.

又因为∠ACO=2∠CDE=30°，所以∠CDE=15°.

因为DE⊥DB，所以∠ADB=75°.

又因为∠DAB=30°，

所以∠ABD=75°，即∠ADB=∠ABD.

所以AD=AB=

综上所述，存在点D使△DEC是等腰三角形，此时AD=2或AD=

【评析】第（1）小题考查基本概念，让大部分学生都能在压轴题上拿分，体现试题对学生的人文关怀.第（2）小题有两种情况，需要分类讨论.由于分类讨论对初中生来说还是一个难点问题，故此题目通过图1（1）和图1（2）暗示形成等腰三角形的两种情况，降低了题目的难度，符合学生思维的发展规律.

2.第（3）小题的解法探究

图2

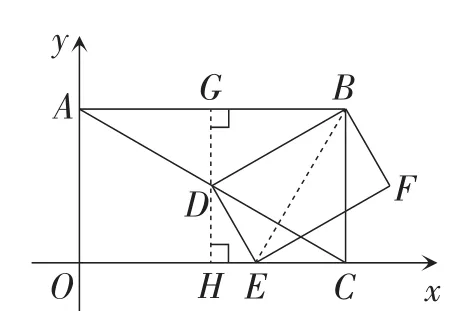
图3

第（3）小题第②问要求用x来表示线段AD的长，并写出矩形BDEF的面积y与x的函数关系式，并求y的最小值.这里题目提示可以用第①问的结论，所以矩形BDEF的面积.又易知则由勾股定理，得DB2=x2-6x+12.从而有.所以当x=3时，y的最小值为.

证明：①如图3，作DH⊥OC于点H，DG⊥AB于点G，

因为四边形BDEF是矩形，

所以∠BDE=90°，即∠HDE+∠GDB=90°.

又因为∠GBD+∠GDB=90°，

所以∠HDE=∠GBD.

又因为∠DHE=∠BGD=90°，

所以△DHE∽△BGD.

因为∠BGH=∠GHC=∠HCB=90°，

即四边形GHCB是矩形，

所以BG=CH.

②因为四边形ABCO是矩形，即AB∥OC，所以∠GAD=∠ACO=30°.

因为DG⊥AB于点G，

在Rt△BGD中，由勾股定理，得DB2=GB2+GD2=

因为矩形BDEF面积y=DE·DB，且

因为AC=2AO=4，即0＜x＜4，

所以当x=3时，y取得最小值为 3.

【评析】第（3）小题第①问通过作垂直构造两个三角形相似来转换所求证的线段比例，这个方法在现行人教版教材的习题中多次出现，学生是比较熟悉的.但是这里要求学生自行构造出辅助线，这对学生的空间想象能力提出了更高的要求，体现出试题“源于教材，高于教材”的命题思路.事实上，这是这道压轴题的难点所在，很多学生都卡在这里，要知道过了这关，最后一问就水到渠成了.如果学生能顺利证明出第①问，最后一问只是将几何问题转换成函数问题.通过第①问的证明结论构造出y与x的函数关系式，然后再通过二次函数得出y的最小值.最后一问没有出现高强度的代数运算，让真正优秀的学生能够脱颖而出，体现了中考数学压轴题考能力、考创新、考发展的价值取向.综观2017年广东省中考数学压轴题，既考查了几何构造，又考查了函数最值，还有分类讨论，比较全面地考查了学生的数学核心素养，是一道难得的好题.

三、试题的拓展

随着对这道中考数学压轴题的深入探究，笔者发现原题目中连接CF后，还有两个重要的问题值得继续探究：一是；二是CF⊥AC.下面笔者将为以上两个拓展问题给出证明.

拓展1：如图4，在原题的基础上连接CF，求证：

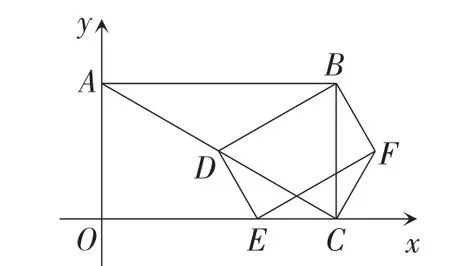
图4

证明：因为，且四边形BDEF是矩形，即DE=FB，

又因为∠DBF=∠ABC=90°，

所以∠DBF-∠DBC=∠ABC-∠DBC，

即∠CBF=∠ABD.

所以△CBF∽△ABD.从而.

拓展2：题干同拓展1，求证：CF⊥AC.

证明：因为△CBF∽△ABD，

所以∠BCF=∠BAD.

又因为四边形ABCO是矩形，即∠ABC=90°，

所以∠BAD+∠BCA=90°.

所以∠BCF+∠BCA=90°，即∠ACF=90°.

所以CF⊥AC.

四、试题的推广

“从特殊到一般，再从一般到特殊”是数学研究的常见用法.将中考数学压轴题的题设与结论推广到一般情况，不仅是将试题的研究升华到一个更高的层次，还能更好地洞察题目的本质和根源，为开展研究性教学提供优质的素材.

题设：如图5，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A(0，b)和C(a，0 )，a＞0，b＞0，点D是对角线AC上一动点（不与点A，C重合），连接BD，作DE⊥DB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF，连接CF.

图5

推论1：当或a时，△DEC是等腰三角形.

证明：如图6，作DH⊥OC于点H，DG⊥AB于点G，

图6

（3） 当DE=CD时，有HE2+DH2=DH2+HC2，即HE=HC，此时点E与点C重合，△DEC不存在.

因为∠DBF=∠ABC=90°，

所以∠DBF-∠DBC=∠ABC-∠DBC，

即∠CBF=∠ABD.

（2）因为∠BCF=∠BAD，且四边形ABCO是矩形，即∠ABC=90°，

所以∠BAD+∠BCA=90°.

则∠BCF+∠BCA=90°，即∠ACF=90°.

所以CF⊥AC.

通过对2017年广东省中考数学压轴题的深入探究与拓展推广，笔者认为此题可作为研究性教学的素材，通过研究试题的解法以优化解题策略和方法，研究试题的拓展与推广以培养学生探究意识和创新精神.