入乎其内 出乎其外——对一道学能检测题的研究

刘 琪

（浙江省景宁畲族自治县启文中学）

王国维认为：入乎其内，故有生气.出乎其外，故有高致.习题教学，深入其中才知其深邃，跳出来更能客观地审视其精髓，并在审视过程中反思提升，有选择地指导自我.笔者以一道九年级学能检测题的教学为例，将教学过程和反思整理成文，与各位同行分享、交流.

题目如图1，在矩形ABCD中，∠BEG=∠BFG=90°，AB=AF.

（1）当EF=2，∠FEG=15°时，求BF的长；

（2）求证：AE=DG.

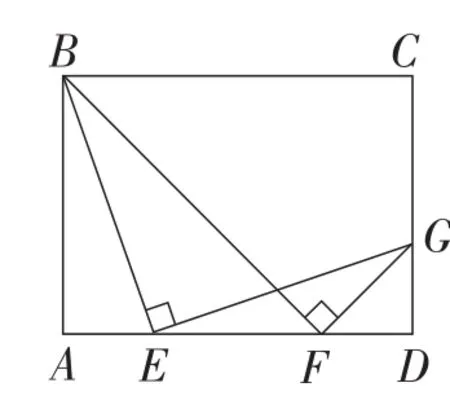
图1

一、研究解法，引导学生一题多解

1.探究基本方法

对于题目的第（2）小题，学生首先想到的解题思路是通过证明三角形全等来证明线段相等，这是由初中学生的知识水平和思维习惯决定的.因此，教师启发学生进行如下思考.

师：从第（2）小题的结论出发，要证明AE=DG，你是怎么思考的？

生1：只要证明△BAE≌△EDG即可.

因为∠A=90°，

所以∠ABE+∠AEB=90°.

因为∠BEG=90°，

所以∠AEB+∠DEG=90°.

所以∠ABE=∠DEG.

因为∠A=∠D=90°，

所以△BAE∽△EDG.

证明至此，生1的思路受阻，教师继续引导学生思考.

师：你的想法很好，通过证明两个三角形全等来说明边相等.现在已经证明了两个三角形相似，只要再证明一组线段相等就可以了，怎样证明呢？

生2：由△BAE∽△EDG，AB=AF，可以根据相似三角形对应边成比例来计算出AE=DG.

设AB=AF=a，DG=x，AE=y，

那么FD=x，EF=a-y.

由△BAE∽△EDG，

因为点E与点F不重合，所以y≠a.

所以x=y，即AE=DG.

师：生2利用相似三角形的性质，通过计算证明了AE=DG.

学生为什么会这样思考呢？由于受到图形特征的暗示，先想到证明△BAE≌△EDG，然而此题要证明这两个三角形全等，却颇费周折，有没有其他方法呢？

师：除了证明△BAE≌△EDG，还有其他方法吗？

生3：可以在△ABE内添加辅助线，构造与△FDG全等的三角形.

师：具体怎么构造呢？

教师巡视并指导，待学生完成证明后，让一名学生讲解.

生4：如图2，在AB上取一点M，使BM=EF.

图2

因为AB=AF，

所以AM=AE，∠AME=45°.

由已知，可得∠DFG=45°.

所以∠BME=∠EFG.

又因为∠ABE=∠DEG，

所以△BME≌△EFG.

所以ME=FG.

从而可证明△MAE≌△FDG.

得AE=DG.

师：证明三角形全等是证明线段相等的常用方法.

“全等法”是证明线段相等的常规思路，要求学生必须掌握.解题后要及时进行反思，看看是否遗漏有价值的线索，从而分析出其他的证明方法.

2.抓住有价值的线索，探索新的解法

证明△BAE∽△EDG后，如果再证明BE=EG，就可得△BAE≌△EDG.所以证明BE=EG成为解题的另一个方向.由于∠BEG=90°，连接BG，只要证明∠BGE=45°即可说明BE=EG.已知∠BFA=45°，所以只要证明∠BGE=∠BFA即可.可以通过证明B，E，F，G四点共圆，再应用同弧所对的圆周角相等证明∠BGE=∠BFA.教师引导学生用“分析法”寻找思路.

师：证明△BAE∽△EDG后，要证明△BAE≌△EDG，还有其他思路吗？

图3

生5：可以通过证明BE=EG来证明AE=DG.如图3，连接BG，只要证明△BEG是等腰直角三角形就可以，也就是证明∠EBG=45°或 者 ∠EGB=45°.可是……

“四点共圆”不是《义务教育数学课程标准（2011年版）》要求的内容，学生要想到这一点很难，所以思路受阻是可以理解的.如果教师进行启发，学生就可以顺势而为，应用四点共圆来证明，这对于优等生和中等生来说正是锻炼思维的好机会.

师：这是一个好思路，让我们一起回到生5刚才的问题，但是怎么证明∠EBG=45°或者∠EGB=45°呢？从已知可得∠AFB=∠DFG=45°.另外，△BEG与△BFG是有公共斜边的直角三角形，它们之间有什么联系呢？

生6：设O为BG的中点.因为直角三角形斜边上的中线等于斜边的一半，所以EO=FO=BO=GO.

教师提示学生画图，找相等的线段.此时圆已经呼之欲出，教师启发学生自己画圆，此时生6补充这些点在同一个圆上.

师：好.下面大家把这个圆画出来（画出图形如图4）.

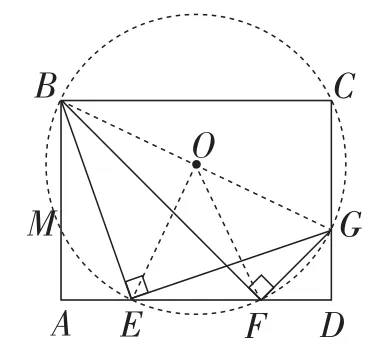
图4

四点共圆是学生思维的难点，也是解题的关键.教学中教师引导学生自己去发现，把圆画出来，接下来就水到渠成了.这是一个创造性的解法，是学生创造性的应用数学知识的体现.“四点共圆法”让此题的已知与未知之间巧妙地贯通起来，一步步引导学生解决问题.研究完问题的解法后，笔者尝试对原题进行改编.

二、改编为开放题，加深理解

笔者通过交换条件与结论、化静为动、将正方形变为矩形等方式对原题进行改编.改编后，原题目的解题方法是否还适用于新问题的解决呢？通过改编原题加深对问题的理解，提高学生综合应用知识的能力.

改编1：交换条件与结论.

（1）如图5，在矩形ABCD中，∠BEG=∠BFG=90°，BE=EG.求证：AE=DG.

（2） 如图5，在矩形ABCD中，∠BEG= ∠BFG=90°，AE=DG.求证：BE=EG.

图5

改编2：化静为动.

如图6，已知AB⊥AF于点A，AB=AF，点E为直线AF上一个动点（点E不与点F重合），过点E，F分别作直线EG⊥BE，FG⊥BF，它们交于点G，GD⊥AF于点D.

（1）如图6（1），当点E在线段AF上时，求证：AE=DG.

（2）如图6（2），当点E在线段AF的延长线上时，AE与DG相等吗？试说明理由.

（3）如图6（3），当点E在线段AF的反向延长线上时，在图中画出图形，猜想AE与DG的大小关系，并说明理由.

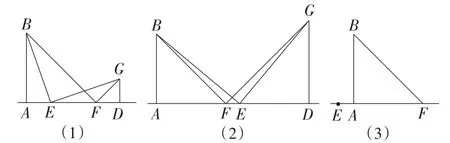
图6

改编3：一般化.

如果把改编2中的“AB=AF”改成“AB=mAF”，其他条件不变，则AE与DG的大小有什么关系呢？试说明理由.

点E在直线l上运动后，图形的形状发生了改变.通过证明三角形全等和四点共圆同样能证明该问题，具体解法在此不做赘述.

改编后的几何探究题对于知识的应用更加综合了.解题中学生体会了知识方法的迁移、分类讨论思想，以及类比思想方法的应用，体验在运动中寻找不变的关系，达到知识应用的融会贯通，从而对原题目的理解更加深刻.如果把几何图形放到平面直角坐标系中，构建函数模型来研究图形的运动，又能观察到什么变化呢？

三、建构函数模型解决问题，揭示本质

运动变化是分类讨论的原因，而初中函数知识也是研究运动的，所以可以把图形置于平面直角坐标系中，通过建立函数模型来研究该问题.于是笔者将问题改编如下.

图7

改编4：如图7，已知AB⊥直线l于点A，AB=a（a是常数，且a＞0），点E是直线l上的一个动点，且EG⊥BE，BE=mEG（m是常数，且m＞0），当点E在直线l上运动时，点G运动的轨迹是什么？并说明理由.

解此题的基本思路是建立平面直角坐标系，先通过作图探求点的运动轨迹，然后设点G的坐标为G(x，y)，通过相似三角形的知识求出y关于x的函数解析式，再验证猜想.

师：当点E运动时，点G的轨迹是什么？同学们是怎么思考的？

生1：可以画出满足已知条件的一些点G，看看运动轨迹是什么？

师：好方法！请同学们试一试.

生2：我画图后发现点G形成的轨迹应该是一条直线（所作图形略）.

师：我们已经通过画散点图发现点G的运动轨迹可能是一条直线，接下来就是进行证明.如果把图形置于平面直角坐标系中，大家认为坐标系应该怎样建立呢？

生3：如图8，分别以直线l、线段AB所在直线为x轴和y轴建立平面直角坐标系.

师：设图8中点G的坐标为G(x，y)，你能求出y关于x的函数关系式吗？如果再设点E的坐标为E(t，0 )呢？

图8

生4：在图8中，过点G作GD⊥Ox，由△BAE∽△EDG，得.所以.化简得到.因为m，a都是不为0的常数，所以也是不为0的常数.所以y是关于x的一次函数，所以点G的运动轨迹是一条直线.

显然这个解答还存在一些问题，因为受图形的暗示，没有从动态思维去看点G的位置，当点G在第三象限或者第四象限时，线段AE，ED，DG长度的代数式是不同的，需要分类讨论.

师：生4应用相似三角形的性质求出了函数关系式，判断了点G的运动轨迹，这就是对函数思想方法的应用.对于这样的推理过程，同学们有没有补充呢？

教师运用几何画板软件演示，点G分别在第三、四象限时停顿，就是图9，图10情形.

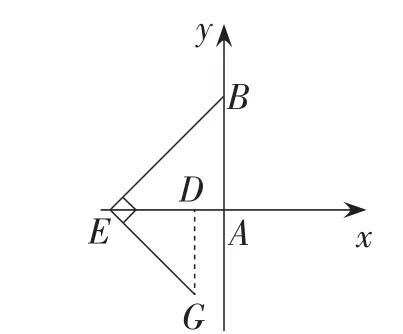
图9

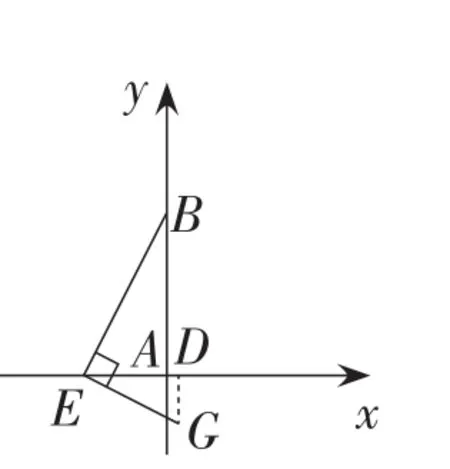
图10

生5：我认为需要分类讨论，当点G分别在第三、四象限时，比例式中这些线段的长度发生了变化，所以当点G分别在第三、四象限时需要重新计算.

师：现在请同学们分别画图计算.

教师巡视课堂，指导学生作图，推理计算，然后请一名学生进行归纳.

生6：当点G在第三象限时（如图9），得.化简得.当点G在第四象限时（如图10），过点G作GD⊥Ox，由已知可证得△BAE∽△EDG，所以.得m.化简得.得到与图9一样的函数关系式.

师：同学们考虑得很全面.改编4是把几何图形放在平面直角坐标系中，通过坐标来研究图形中的点、线段和角的关系，这是一种重要的数形结合的方法.下面我们应用函数的性质再做一些分析，看看能够得到什么结论？

生7：由直线的解析式可以求出直线与坐标轴的交点，与x轴、y轴交点坐标分别是

为了启发学生发现新结论，教师画出这条直线（如图11），并标上两个点的坐标.

师：请同学们求出点E的坐标及线段AF，ED，DG的长，你有什么发现？

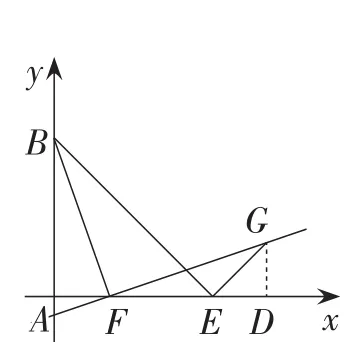
图11

生8：由，可以得AF=，ED=x-所以AF=ED.

通过应用函数的性质分析，学生发现了一个重要的结论，即图形中存在一个不变的等量关系AF=ED.

师：那么当点G分别在第三、四象限时候（图12，图13的情形），结论还成立吗？你还有什么发现吗？

图12

图13

生9：结论成立.我发现求出函数解析式后，图形中的线段长度都可以用代数式表示.当m=1时，就是刚开始研究的习题；当m≠1时，就是后面的改编题；而且它们之间是可以联系起来的，就是特殊与一般的关系.

师：生9总结的很到位.回顾整个解题、改编习题的过程，证明线段相等或者倍分关系，构造全等三角形或者相似三角形是基本方法；把几何图形放到平面直角坐标系中，建立函数模型，应用数形结合思想进行求解，为解题确立了一个新的方向，应用函数的性质，揭示了习题的本质，发现了重要的结论，而且可以把这些习题联系并且统一起来.

四、反思

习题的研究应当从解法开始，探索符合学生认知水平和思维习惯的解题方法，并归纳出通性、通法，如原题中的证明三角形全等或者三角形相似.教学中要求学生必须掌握这些基本方法，这是教学的重点所在.同时教师要精心设计问题，引导学生独立思考，自己发现解法，动笔画图、大胆发言，以及推理计算等.

解题后要进行反思，进行一题多解或者改编.如原题根据证明△BEG是等腰三角形，从而发现了四点共圆法，让解题找到了新的方向，也创造性的应用了圆的知识，培养学生的创造性思维能力.改编原题，如通过交换原题的条件与结论、把原题改编为开放题、一般化问题等方式，培养学生综合应用知识、探索问题的能力.

教师可以对原题做更深入的研究，进而揭示题目的本质.例如，改编4中，在几何图形中建立直角坐标系，构造一次函数模型研究题目，既应用了相似三角形性质和一次函数的知识，并用代数方法解决几何问题，又揭示了问题本质.同时也可以把各题统一起来，把初中的一些主干知识、数学思想方法结合起来.一方面，为学生渗透了用函数思想研究几何问题的方法，与高中解析几何衔接起来；另一方面，应用习题研究成果进行培优，发展学生的应用意识和解决问题的能力，让不同的学生得到充分的发展，实现经济高效的课堂教学.