乐学：问题导学的应然追求

李 军

（江苏省宿迁市实验学校）

乐学一词始见于《礼记·学记》之“不兴其艺，不能乐学”.它是学习者自觉、能动、积极、愉悦的学习状态，与乐学相对的是浅学、苦学、厌学、不会学等.乐学境界是学习者在学习中发现、享受、创造和传递快乐的思想觉悟和精神修养.孔子所言“知之者不如好之者，好之者不如乐之者”，则是对乐学学习境界价值追求的最好诠释.

一、乐学的心理分析

美国心理学家戴维·迈尔斯指出，乐观主义是追寻生命意义和幸福的法宝.学生乐学的心态能够帮助个体用更加客观的视角看待学习与生活，面对真实的人生，从而获得解脱和超越.从乐学的个体价值来看，坚持正向引导及乐观积极的心态具有重要的意义.

乐学是一种指向未来的积极认知（学习）倾向，属于个体的信念系统.有学者认为，乐观可能是一个高度有利的心理特征，它与人们好的心情、坚持不懈、成就和身体健康有关.由此看出，乐学是教育价值观念中应普遍重视的学习品质，是推动个体进步与发展的文化机制.

乐观的学习可以通过教育而形成，当前对学生乐观心态的培养程序主要由认知训练和行为训练两部分组成.认知训练主要包括四个步骤：一是分析情绪变化的情境；二是从解释风格的三个维度分析信念；三是找出情绪变化情境的其他可能解释，并评估其依据；四是与悲观主义思维进行辩论.行为训练包括放松和应对技巧训练、社会技巧训练、谈判技巧训练、问题解决训练等.

二、乐学的导学分析

问题导学是以问题为载体来引领、指导学生的学习，从而达成将内容本位转向学生本位的教学.而人天生是趋乐避苦的，这就要求教师在进行问题教学的同时，要更多地关注学生的学习状态，唤醒学生的内部动力，以学习兴趣为根本指向，追求有效学习、快乐学习，更好地促进师生共同成长，愉快和谐发展.

1.活化多元性问题，让学生主动“乐说”

活化问题就是通过灵活多元（一题多问、多思、多解、多图等）的问题设计，激活学生思维，启发学生的表达欲望，实现一吐为快的满足感.这里需关注以下几点：（1）营造和谐的学习氛围，让学生在轻松愉快的环境中表达；（2）问题设计要有整体性、灵活性、开放性的特点，做到能放可收；（3）问题要符合学生的最近发展区，突出学生主体、教师主导、问题主线的“三主”原则，让学生能主动地表达，等等.

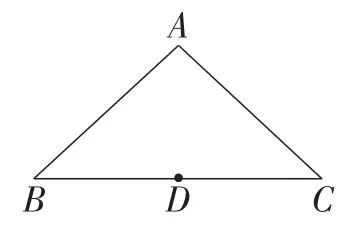
图1

案例1：全等三角形的判定教学片断.

问题：如图1，在△ABC中，AB=AC，D是BC中点，在AB，AC上确定点E，F，使△DBE≌△DCF，你有什么办法呢？并说明你的理由.

师：通过分析，针对需解决的问题，其实我们已经知道了一组边和一组角对应相等，下面请大家畅所欲言，给出一些符合判定定理的作法.

生1：过点D分别作DE⊥AB，DF⊥AC，垂足分别为点E，F，利用全等三角形判定方法“AAS”来说明△DBE≌△DCF.

生2：过点D分别作DE⊥AB，DF⊥AC，垂足分别为点E，F，连接AD，可利用直角三角形全等的判定方法“HL”来说明△DBE≌△DCF.

生3：过点D分别作DE∥AC，DF∥AB，分别交AB，AC于点E，F，利用全等三角形判定方法“ASA”来说明△DBE≌△DCF.

生4：在BA上截取BE，在CA上截取CF，使BE=CF，利用全等三角形判定方法“SAS”来说明△DBE≌△DCF.

生5：作 ∠BDE=∠CDF分别交BA，CA于点E，F，利用全等三角形判定方法“ASA”来说明△DBE≌△DCF.

生6：以点D为圆心画弧，分别交BA，CA于点E，F，利用全等三角形判定方法“SSA”说明△DBE≌△DCF.

生7：我认为生6的说法不对.我试着画了一下图形（如图2），以点D为圆心画弧分别交BA，CA于点E，F时，并不能说明△DBE≌△DCF.因为“SSA”是假命题，不能说明两个三角形全等.

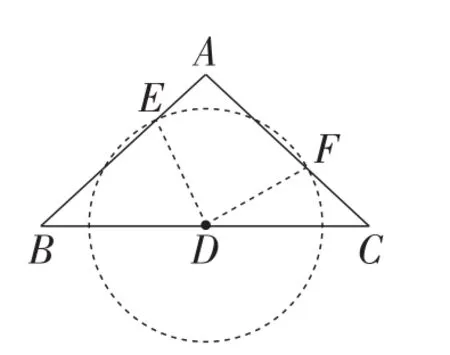
图2

师：很有说服力！生7不仅思考了，还画出了图形，并说明了理由.请同学们一定要注意，“SSA”及“AAA”不能判断两个三角形全等.

导学分析：初中生正值青春发育期，心理敏感而脆弱，内心渴望得到认可、尊重与信任，经受不起挫折、嘲笑与打击等，因此在众人面前，不愿意表达自己的见解.教学中，时常会出现学生不愿意回答或不敢回答问题的尴尬场面.其实，通过创设问题情境，活化问题，多元求通等，不拘泥于一问一答式的窄化学生思维的教学方式，便可慢慢打开学生“乐言”之闸.参与其中方能感受到快乐，快乐交流便能掌握知识、发展能力、提升素养、增长智慧.

导学时，教师要基于以下几点思考：（1）言之有物，即给出一定的问题条件（如问题中的边与角），搭建话语平台，让学生有抓手，睹物思言、畅所欲言就能水到渠成；（2）言之有序，就是要明晰已知与未知关联之序，或是图形变化之序，或是特殊与一般之序等，构建层次序列，实现清晰表达；（3）言之有据，表达时，始终围绕全等三角形的判定方法“SAS”“ASA”“AAS”“HL”展开，培养学生言之有据的说理习惯.

2.趣化操作性问题，让学生主动“乐做”

裴光亚先生认为，教师在课堂上最应该做两件事，其中之一就是激发学生的求知欲和好奇心.操作探究则是唤醒学生认知兴趣的重要抓手.因此，趣化操作类问题，可催发学生的动手欲望，激发学习热情，引发数学思考，继而提升数学学科的核心素养.

案例2：黄金分割教学片断.

在进行黄金分割内容的教学时，教师先介绍了定义，接着得出黄金分割比，并介绍了黄金分割在生活中的应用，学生感到很有趣.当进行到从形的角度画黄金分割点时，采取小组合作方式，学生探究的热情高涨，有的查书，有的讨论，有的先简单画图，有的还做出了模型，乐此不疲，争先恐后，认真讨论、总结、创新.接着，学生在教师的引导下完成了在正方形纸片的边长上折出黄金分割点，并进行了计算验证.

作法：如图3，用一张正方形纸片ABCD，先对折，得到E为边CD中点，将AE折叠到AB上，折痕为AH，则H就为边CB的一个黄金分割点.

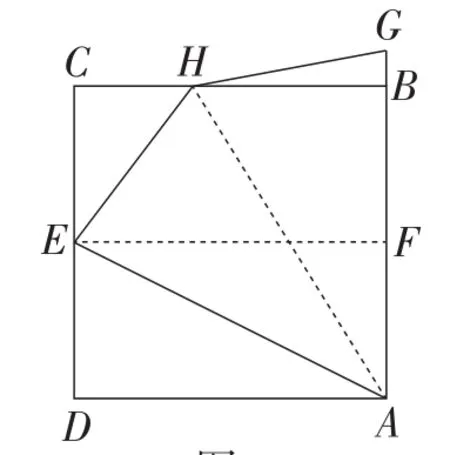
图3

导学分析：操作性问题就是强调重视实践操作，在“做”中学.《义务教育数学课程标准（2011年版）》指出，数学活动经验需要在“做”的过程和“思考”的过程中积淀，是在数学学习活动过程中逐步积累的.长期以来，有些学生习惯于听，而忽略“做”或懒于“做”，成为课堂上的看客或听众，被动或被迫学习，效果可想而知.上述教学中，教师通过精心设计有趣的操作性问题，让学生动手操作，在画图、折纸等过程中，加深了学生对知识的理解，获得了直观感受，引发学生积极思考，在“做数学”的主动探究过程中培养学生的动手能力和解决问题的能力，进而培养学生的创新精神.同时，让学生获得快乐的体验，达到乐学的功效.

3.深化基础性问题，让学生主动“乐问”

深化基础性问题就是将基础知识或基本模型进行适时的变式、深化探究，不让能揭示本质的数学问题轻易流失，珍视好的教学资源，发挥问题的启思功能，激发学生互议互问，善问乐问，从而获得解决问题的成就感.

案例3：勾股定理“总统证法”模型探析.

图4是美国第二十任总统伽菲尔德对勾股定理的证法的图形，也称总统证法.从表层来看，它可以证明勾股定理.当教师让学生进一步观察、深化图形的研究时，学生提出了诸多见解，概括起来有如下收获.

图4

图5

（1）图4的证法图可以看成毕达哥拉斯勾股图（如图5）的一半，两者有相通之处，利用面积关系均可证明勾股定理.

（2）图4的模型图为直角梯形，其中含有两个全等的直角三角形和一个等腰直角三角形，隐藏着正方形；蕴含着角相等、角互余、角互补、线垂直、线平行、三角形全等多种关系.

（3）在学生发问的基础上，探究了若以AE为直径画☉O，☉O与直线CD的位置关系为☉O与直线CD相交（如图6）.当b=a时，☉O与直线CD相切.

图6

（4）还可探究以CD为直径的圆与直线AE的位置关系等.

导学分析：对于浅层次的问题，学生是不屑询问的，而太难的问题又不愿意去问.面对两难境地，教师必须浅处搭台、深处挖掘，让基础性问题慢慢生长，让学生有爬坡之感.

德国教育家第斯多惠说，科学知识不应该是传授给学生，而应当是引导学生去发现它.这就是说，教师的重要任务是启发和引导学生拥有强烈的求知欲和浓厚的学习兴趣.“乐问”实际上就是一个有效的学习过程，它是一种参与、在场的态度.上述案例中，教师搭建了一个基本模型，引发师生共同思考，通过问题引领、变式探究，得到很多有意义的收获，将教学置于“乐问”情境中，超越预设，生成更多的精彩.

4.点化易错性问题，让学生主动“乐思”

学习是从未知走向已知的过程，学生在解答问题的过程中，难免会出现这样或那样的错误.点化错误问题，就是针对学生亲自体验过的，而又暂时没有顺利解决的问题，教师给予点拨、指导、启发，让学生再深入思考，形成反思能力，不断体会、顿悟，使之迈向成功.

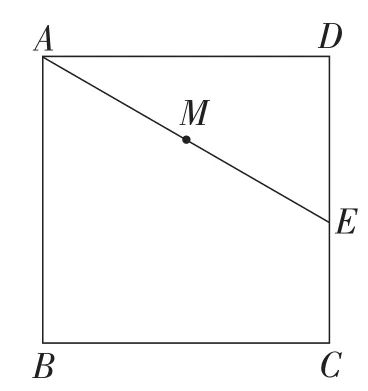
图7

案例4：一道中考试题的求解.

题目（2014年江苏·泰州）如图7，正方向ABCD的边长为3 cm，E为CD边上一点，∠DAE=30°，M为AE的中点，过点M作直线分别与AD，BC相交于点P，Q.若PQ=AE，则AP的长为_____.

错解展示：此题也是苏科版《义务教育教科书·数学》九年级上册第1章第26页习题的变式.学生看到题目后，直观上以为是教材上的问题，感觉很熟悉，从而放松对问题的深度思考，很快画出了图形（如图8），加之受解题思维定势的影响，由PQ=AE构造全等三角形，得PQ⊥AE.再用解直角三角形知识，得出AP=2.

图8

点化引思：基于上述问题，教师通过以下问题给予适时针对性点化，让学生乐于再探究、再思考.

问题：（1）请同学们进一步化无形为有形，即构图思考；（2）让静态的图形动起来思考，即将PQ绕点M旋转，是否有新的发现？（3）变换一种方式再思考：从轴对称视角，是否存在一条线段经过点M且与线段PQ成轴对称？

完善纠错：学生经过教师点拨后自发地展开了激烈的讨论，完善了上述的解答，将其整理如下.

图9

由题意画出图形（如图9），过点P作PN⊥BC，交BC于点N，得到AD=DC=PN.在Rt△ADE中，利用锐角三角函数定义，求出DE的长为，再由勾股定理求出AE的长是c m.根据全等三角形对应边、对应角相等，得到DE=NQ，∠DAE=∠NPQ=30°.再由PN与DC平行，得到∠PFA=∠DEA=60°.进而得到PM⊥AE.在Rt△APM中，根据AM的长，利用锐角三角函数定义求出AP的长为2 cm.再利用对称性确定出AP′的长为1 cm.综上，AP等于1 cm或2 cm.

导学分析：初中生受知识、经验和方法的局限，课堂上出现各种各样的错误实属正常现象，特别是对于分类型多解类问题，学生往往考虑不周，回答不全.哲学家黑格尔先生说得好，错误本身乃是达到真理的一个必然环节.错误是重要的教学资源，它的价值关键在于让师生能从中得到启迪，生成更多的思考.因此，要善待和珍惜学生的错误，要能在点化错误与纠错中生长智慧，积累更多的经验.通过上述问题的引导、点拨、反思，学生不断分析探究，琢磨解题策略，提炼解题方法，收获良多.例如，学生会养成画图分析问题的习惯，化无形为有形，化内隐为外显；让图形动起来思考问题；关注特殊分析问题（垂直、平行、30°等）；图形给出不完整时要想到分类，学会分类讨论，等等，真可谓吃一堑，长多智.

三、结束语

有问题才会有思维；有问题，才会有求异；有问题，才会有创新.教师可通过问题设置引导学生“乐言”“乐做”“乐问”“乐思”，把学生问题意识的培养落到实处，这是教师教会学生主动学习的重要方法之一，也是促进学生智能发展和素质提高的重要途径.总之，学生只有主动参与学习，才能体会到学习的乐趣，主动乐学是师生不懈地应然追求.