利用二部图生成概念格
2018-09-18窦林立展正然
窦林立,展正然
形式概念分析又称概念格[1-2],是由德国Wille教授在20世纪80年代首次提出的,它提供了一种支持数据分析和知识处理的数学工具[3-4]。近些年来,国内外各位学者提出了许多的构造算法。例如:Godin等[5]提出了概念格的渐进生成算法;Ho[6]提出了基于概念格的概念聚类算法;张文修等[7]给出了在保持格同构的条件下建立概念格的属性约简的方法;Elloumi等[8]基于模糊形式背景建立了一个多层次的约简理论。
近几年许多学者从图论方面对概念格进行研究。例如:Amilhastre 等[9]与 Berry 等[10-12]将二部图与概念格进行了交叉研究;李立峰等[13-14]利用弦二部图和链图对概念格进行表示;张涛等[15-17]利用属性树和属性拓扑图来表示形式背景,简化了形式背景的表示结构,并提出了基于树图的属性约简算法。本文通过二部图的极大完全子图的概念来生成概念格,给出了基于二部图的深度优先的概念格的迭代算法。
1 基本概念
本节主要介绍概念格与二部图的基本知识。关于概念格的更多内容参见文献[1,18],有关图论的详细内容参见文献[19-20]。
1.1 概念格
定义1 1)在形式概念分析中,一个形式背景是一个三元数组,其中O是对象集合,M是属性集合,I是O与M之间的一个二元关系。用表示“对象有属性” 。对于及, 定 义 :,。则形式背景的概念定义为元素对,其中,,,。概念的外延是A,内涵是B。
通过上述两种方法约简形式背景后,就可以有效地减少形式背景中属性集合中的元素个数,从而降低生成概念格的难度,更迅速地生成概念格。
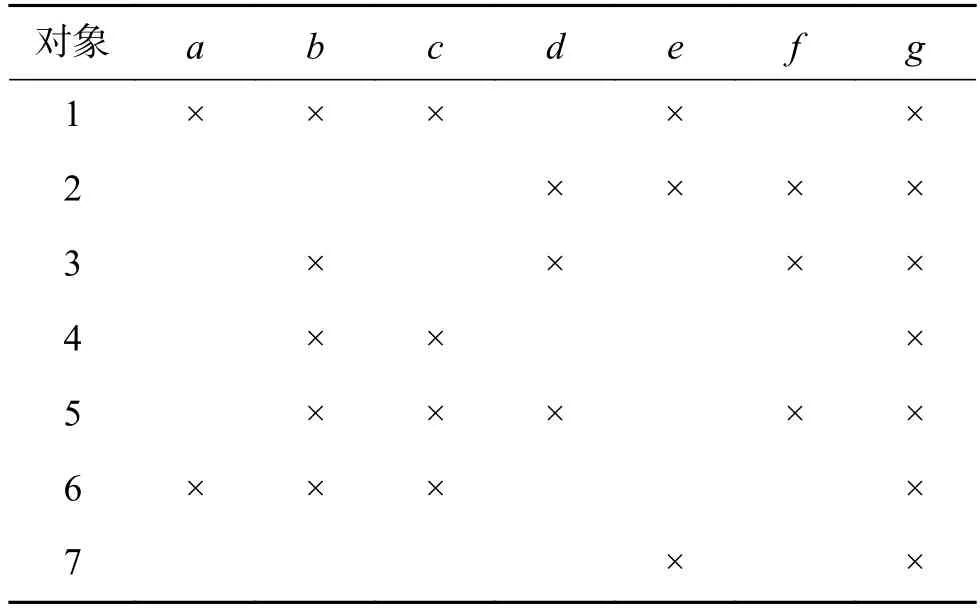
表1 形式背景(O,M,I)Table 1 Formal context (O,M,I)
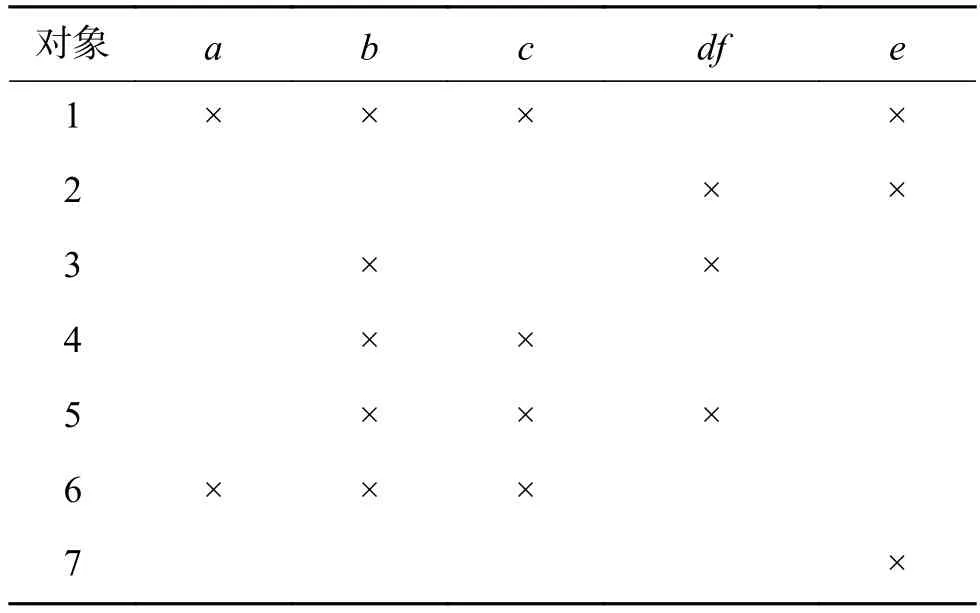
表2 约简后的形式背景(O,M,I)Table 2 Reduced formal context (O,M,I)
1.2 图论
由概念格和二部图的定义可知,每个形式背景都对应一个二部图,其中二部图的顶点集为,顶点与之间有一条边当且仅当与满足关系I。
下面用具体实例来说明以上定义。
例2 图1是例1中约简后的形式背景表2对应的二部图,图2是表2对应的概念格,原形式背景表1对应的概念格即为图3。

图1 表2对应的二部图Fig. 1 Bipartite graph for table 2
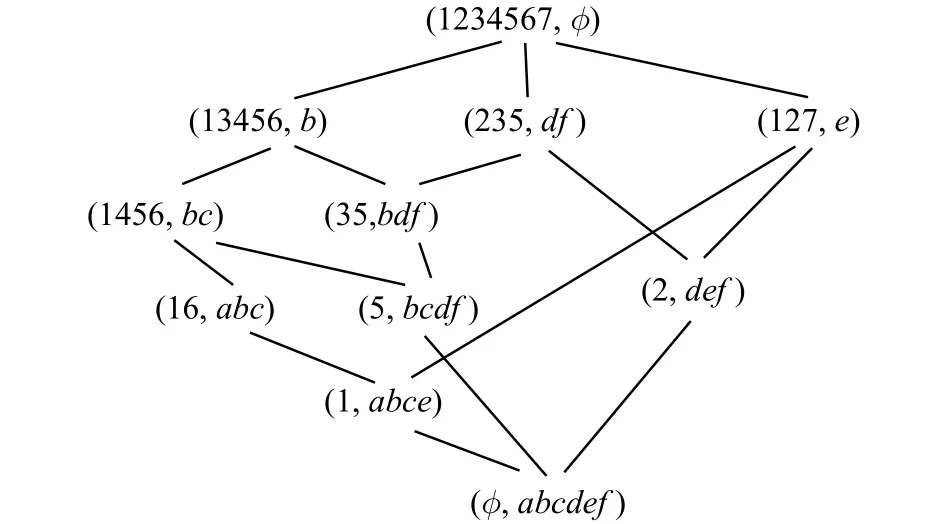
图2 表2对应的概念格Fig. 2 Concept lattice for table 2
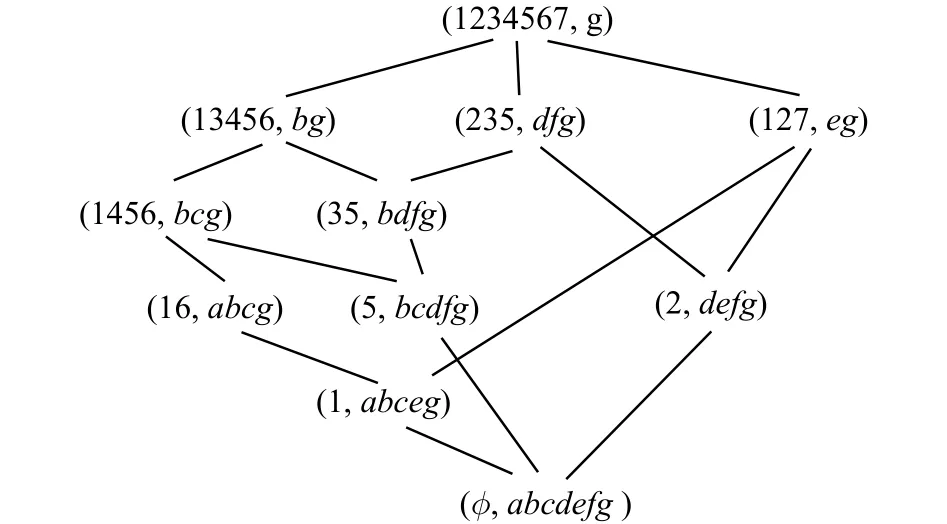
图3 表1对应的概念格Fig. 3 Concept lattice for table 1
2 利用二部图生成概念格
形式背景中的数据,在很多情况下,对象的个数较大,而属性的个数则相对较少,在这种情况下,基于属性来生成概念格,可以有效地减少算法的执行时间。本文基于属性,利用二部图子图和邻集的知识来生成概念格。
本节中的形式背景是指约简后的形式背景,二部图也指约简后的形式背景所对应的二部图。
首先给出二部图的极大完全子图的定义。
定义4 若 S 是二部图 G 的子图,且 S是完全二部图,对任意的 v ∈V(G)−V(S), G 由 V (S)∪v导出的子图 G [V(S)∪v]不是完全二部图,则 S称为二部图G的极大完全子图。
下面给出二部图的极大完全子图与概念的对应关系。
证明 由概念格的定义知充分性显然成立。
下面的定理2和定理3就是利用二部图的极大完全子图得到顶层概念 (O ,ϕ)的直接子概念。
定理2 形式背景 K =(O,M,I)对应的二部图为G=(O,M;E),i 为图 G 的顶点集 M 中度数最大的顶 点 , N(i)=P ,则i 与 P 构 成 的 G 的 导 出 子 图G[P∪i]是 G 的极大完全子图,即 (P ,i)为概念,且(P,i)为顶层概念( O ,ϕ)的直接子概念。
证明 用反证法。假设 G [P∪i]不是 G的极大完全子图,即存在 o ∈O−P ,有 S1=(P∪o,i;E1)为完全二部图,或存在 m ∈M,有 S2=(P,i∪m;E2)为完全二部图。若有第一种情况,则顶点 i 与 P ∪o相邻,此与 N (i)=P矛盾。若有第二种情况,由完全二部图的定义知 i ∪m与P中每个顶点都相邻,如果m的邻集恰好为P,则i与m应约简为im,与i和m是两个顶点矛盾;如果m的邻集包含P,即至少存在 o1∈O ,使 m 与 P ∪o1相邻,则 m 的度数大于i的度数,此与i为 M 中 度数最大的顶点矛盾。因此,G[P∪i]是G的极大完全子图,即 (P ,i)为概念。且其为顶层概念 (O ,ϕ)的直接子概念,因为不存在概念 C ,使(P,i)<C < (O,ϕ)。
定理3 若 j 是形式背景 K =(O,M,I)对应的二部图 G =(O,M;E)的顶点集 M 中除i外度数最大的顶点, N (j)=P∗。若 P∗⊄ P ,则 (P∗,j)为顶层概念(O,ϕ)的直接子概念;若 P∗⊂ P ,则以 P∗为外延的概念应为 (P ,i)的子概念。
证明同定理2。
证明 (P ,i)为形式背景 K 的概念, ( Q,j)为形式背景 K∗的概念,前文已证。下证 (Q ,i∪j)为形式背景 K 的概念,即需证 G Q,i∪j 为二部图 G 的极大完全子图。
用反证法。假设 G Q,i∪j 不是二部图 G 的极大完全子图,那么可能有下列两种情况:1)至少存在 o ∈P−Q,使 G Q∪o,i∪ j为完全二部图;2)至少存在 m ∈M−i−j ,使 G Q,i∪ j∪m为完全二部图。如果出现第一种情况,由完全二部图的定义知在图 S 中顶点 j 与 Q ∪o中的每个顶点相邻,此与在形式背景 K∗中 N (j)=Q矛盾。如果出现第二种情况,由完全二部图定义知在图S中m与集Q中的每个顶点相邻,那么m在S中的邻集必包含j在S中的邻集,这与形式背景已约简且j是S的顶点集中 度数最大的顶点相矛盾。所以为形式背景K的概念,并且不能找到集合B,使,因此 (Q ,i∪j)是( P ,i)的直接子概念。
根据定理4可以通过求 G 的导出子图的概念来简化形式背景,并求出 (P ,i)的直接子概念。这样经过反复的分解和约简,使形式背景越来越简化,同时也能求出的所有子概念。
因此便能生成顶层概念的所有直接子概念以及它们各自的子概念。这便是基于二部图的深度优先的概念格的迭代算法。
基于二部图的深度优先的概念格的迭代算法:
1) 最顶层概念为 (O ,ϕ),标号为1。
2) 形式背景 K =(O,M,I)(约简后),其对应的二部图为 G =(O,M;E),取属性M中度数最大的顶点i , N (i)=P ,则 (P ,i)为顶层概念 (O ,ϕ)的直接子概念,标号为21。
3) 画出 G 的导出子图 S1=G[P∪(N(P)−i)](约简后),其对应的形式背景为 K1。取二部图 S1的属性集 N (P)−i 中度数最大的顶点 i1, N (i1)= P1,则(P1,i1)为形式背景 K1的概念, ( P1,i∪i1)为形式背景K 中概念 (P ,i)的直接子概念,标号为31。
4) 画出 S1的导出子图S2=S1[P1∪(N(P1)−i1)](约简后),其对应的形式背景为 K2,取二部图 S2的属性集 N (P1)−i1中度数最大的顶点 i2, N (i2)=P2,则 (P2,i2)为形式背景 K2的概念,故 (P2,i∪i1∪i2)为形式背景K中概念 (P1,i∪i1)的直接子概念,标号为41。继续下去,直到 Pl为 单点集,则(Pl,i∪i1∪i2···∪il)为形式背景K的倒数第二层概念,它由导出子图Sl生成,其直接子概念为最底层概念 (ϕ ,M),标号为 (l +2)1,最底层概念 (ϕ ,M)的标号为 l+ 3。
5) 从标号为 r1 的概念回到生成它的导出子图Sr−2,考察二部图 Sr−2的属性集中未考虑过的度数最大的顶点 ir−2∗。如果 N (ir−2∗)=Pr−2∗是已生成的概念的外延,且当此已生成概念的内涵包含i∪i1∪i2···∪ir−2∗时,说明以 Pr−2∗为外延的概念及其子概念已生成,则不必再考虑此顶点;而当此已生成概念的内涵等于时,则是的直接子概念,且此概念及其子概念已生成(已标号),此顶点也不必再往下考虑。如果 Pr−2∗不 是 已 生 成 概 念 的 外 延 , 则 (Pr−2∗,ir−2∗)是(Pr−1,ir−1)的直接子概念,标号为 (r −1)2,然后按步骤3)和步骤4)的方法画出 Sr−2的导出子图Sr−1∗=Sr−2[Pr−1∗∪ (N(Pr−1∗)− ir−1∗)],接着再取未考虑过的最大度数顶点生成概念,直到倒数第二层概念。
3 实例
下面通过例3来具体说明此方法如何产生概念格。
例3 形式背景同例1,其中的对象O={1,2,3,4,5,6,7}表示1班至7班共7个班级,属性M={a,b,c,d,e,f,g}表示班级特色,其中a表示团结,b表示纪律严明,c表示学风端正,d表示卫生环境好,e表示干部队伍过硬,f表示英语四六级通过率高,g表示课余活动丰富。
下面用基于二部图的深度优先的概念格的迭代算法来生成概念格。
1) 最顶层概念为 (1 234567,ϕ),标号为1。
2) 画出形式背景(约简后)所对应的二部图G,其属性中度数最大的顶点为 b ,N(b)={1,3,4,5,6},故 (1 3456,b)为 (1 234567,ϕ)的直接子概念,标号为21。
3) 画出 G 的由 P ={1,3,4,5,6}和 N (P)−b={a,c,df,e}导出的子图 S1,二部图 S1的属性集中度数最大的顶点 c , N (c)={1,4,5,6},故 (1 456,bc)为(13456,b)的直接子概念,标号为31。
4) 画出 S1的由 P1={1,4,5,6}和 N (P1)−c={a,df,e}导出的子图 S2,二部图 S2的属性集中度数最大的顶点 a , N (a)={1,6},故 (1 6,abc)为 (1 456,bc)的直接子概念,标号为41。画出 S2的由 P2={1,6}和N(P2)−a={e}导出的子图 S3,二部图 S3的属性集中度数最大的顶点 e , N (e)={1},故 (1 ,abce)为(16,abc)的直接子概念,标号为51。此时 P3={1}为单点集,故 (1 ,abce)为倒数第二层概念,其直接子概念只有 (ϕ ,abcdef), ( ϕ,abcdef)为最底层概念,标号为6。
5) 从标号为51的概念 (1 ,abce)开始返回到生成它的二部图 S3,其属性集中除 e外无其他顶点。所以返回到标号为41的概念 (1 6,abc)的二部图 S2,其属性集中除 a 外还有顶点 d f 和 e 。先看 d f,N(df)={5},未出现过以5为外延的概念,故(5,bcdf)为 (1 456,bc)的直接子概念,标号为42,此时P2∗={5}为单点集,故 (5 ,bcdf)为倒数第二层概念,其直接子概念只有 (ϕ ,abcdef)。再看 e , N (e)={1},已出现过以1为外延的概念 (1 ,abce),且其内涵 a bce真包含 b ce,故此处不再考虑。
现在返回到生成标号为31的概念 (1 456,bc)的二部图 S1,其属性集中除 c 外还有顶点 a ,df,e。其中N(a)={1,6}, N (e)={1},已出现过以16和1为外延的概念 (1 6,abc)和 (1 ,abce),且其内涵真包含 a b和be ,故此二顶点不再考虑。而 N (df)={3,5},未出现过以35为外延的概念,故 (3 5,bdf)为 (1 3456,b)的直接子概念,标号为32。然后接着画出 S1的由P1∗={3,5}和N(P1∗)−df={c}导出的子图 S2∗∗,二部图S2∗∗的属性集中度数最大的顶点为 c , N (c)={5},已出现过以5为外延的概念 (5 ,bcdf),此概念的内涵恰好为 b cdf ,则 (5 ,bcdf)也为 (3 5,bdf)的直接子概念,此顶点不再考虑。
现在返回到生成标号为21的概念 (1 3456,b)的二部图 G ,其属性集中除 b外 ,还有 a、 c 、 d f 和 e。其中N(a)={1,6},N(c)={1,4,5,6},已出现过以16和1456为外延的概念 (1 6,abc)和 (1 456,bc),且其内涵真包含 a和 c,故此二顶点不再考虑。 N (df)={2,3,5},未出现过以235为外延的概念,故 ( 235,df)为(1234567,ϕ)的直接子概念,标号为22。然后接着画出 G 的由 P∗={2,3,5}和 N (P∗)−df = {b,c,e}导出的子图 S1∗,二部图 S1∗的属性集中度数最大的顶点为b,N(b)={3,5},已出现过以35 为外延的概念 (3 5,bdf),此概念的内涵恰好为 b df ,则 (3 5,bdf)也为(235,df)的直接子概念,此顶点不再考虑。 S1∗的属性集中除 b 外,还有 c 和 e , N (c) = {5},已出现外延为5的概念 (5 ,bcdf),且其内涵真包含 c df,故此顶点不再考虑。 N (e)={2},未出现过以2为外延的概念,故(2,def)为 (2 35,df)的直接子概念,标号为33。此时其外延 P1∗={2}为单点集,其直接子概念只有(ϕ,abcdef)。
返回二部图 G 中的属性 e , N (e)={1,2,7},未出现过以127为外延的概念,故 (1 27,e)为(1234567,ϕ)的直接子概念,标号为23。接着画出G的由P∗∗={1,2,7}和N(P∗∗)−e={a,b,c,df}导出的子图 S1∗∗,二部图 S1∗∗的属性集中 a 、b 、c的邻集相等,约简后属性集中度数最大的顶点为 a bc 和 d f , N (abc)={1},N(df)={2},已出现过以1和2为外延的概念(1,abce)和 (2 ,def),其内涵恰好为 a bce 和 d ef,则(1,abce)和 (2 ,def)也为 (1 27,e)的直接子概念,此二顶点不再考虑。
到此已生成所有概念,见图4。其概念格见图3。
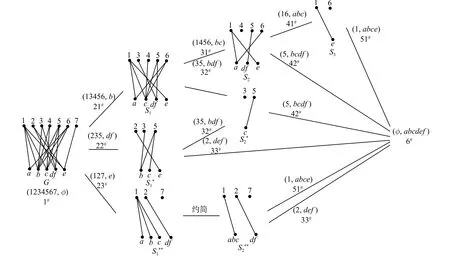
图4 生成概念格的过程Fig. 4 Process of generating concept lattice
4 结束语
本文结合图论的内容,将概念格的形式背景和一个二部图相对应,利用二部图的极大完全子图来寻找概念,并且同时得到概念之间的父子关系,最终构造出概念格。此方法同时生成Hasse图,简单直观,能够快速生成概念格。基于概念格的形式背景与图论内容的高度关联性,二者之间其余理论的相互应用是我们下一进努力的方向。
