瞬变流速作用下姿控发动机燃料管路的非线性振动特性分析
2021-03-02何志勇张志峰宋少伟
何志勇,张志峰,宋少伟
(1. 西安航天动力研究所,陕西 西安 710100; 2.长安大学 “道路施工技术与装备”教育部重点实验室,陕西 西安 710064)
0 引言
输送流体的管道广泛应用于航空航天工程、石油能源工业、动力水能工业以及核工业等领域。由于输送泵泵送原理、管道变径或弯曲等原因,导致流体在管道输送过程的压力[1]、流速[2]发生周期性波动或随机波动,这种波动会致使管道产生剧烈振动,甚至可能诱发管道发生共振,从而导致比较严重的系统失效,或发生灾难性事故。因此,输送流体管道的模型建立与振动特性分析一直受到专家学者的重点关注。国内外学者分别从管道材料[3]、载荷类型[4]、管道形状[5-6]、流体参数[7-9]等方面,利用数值模型[10-13]、有限元分析[14-16]、试验测试[17]等方法对流固耦合的流体管路进行振动特性研究,揭示了一些典型流体输送管道的振动机理,并提出了一些有效的预防措施,确保了流体输送管道的可靠性。
卫星姿控采用挤压式发动机,对其工作稳定性、可靠性要求均很高。如杨林涛[17]分析了姿控发动机燃烧室燃烧不稳定振荡对燃料输送管路振动的影响,但关于电磁阀门开启、闭合时长导致输送液路流速变化对燃料输送管路的振动影响的研究尚未见到。本文建立了瞬变流速作用下姿控发动机燃料管路的非线性液固耦合振动模型,用于研究管路电磁阀开启或关闭时长引起的液体瞬时速度变化对燃料管路的振动响应特性,以便为减弱卫星姿控发动机燃料输送管路的不稳定振动提供理论依据,以期对提高姿控发动机的可靠性有所帮助。
1 管路模型分析
某型姿控发动机系统由气瓶、贮箱、减压阀、电磁阀、燃烧室和管路等组成,燃烧室燃料入口管路示意图如图1所示。
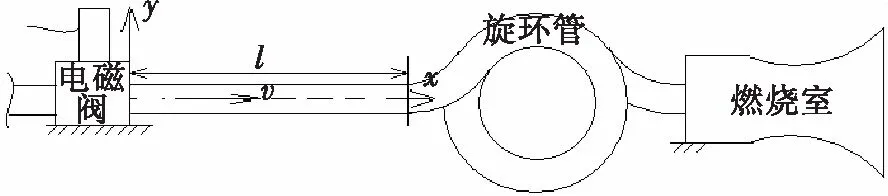
图1 管路分析理论模型Fig.1 Analyzed model of pipeline
电磁阀开启、关闭时,姿控发动机燃料瞬变流会激励管路(电磁阀到卡箍处之间管路)振动。由于旋环管具有大柔度,直线型管路会产生大位移横向振动现象。为简化管路分析模型,只考虑燃料瞬变流速对直线型管路(电磁阀到卡箍处之间管路)振动特征的影响,将管路电磁阀门端设为固定约束,旋环管设为非线性弹簧对直线型管路另一端进行横向位移约束,分析管路受到的非线性弹簧反力
f=(k1y+k2y3)δ(l)
(1)
式中:l为直线型管路长度;k1、k2为非线性弹簧刚度系数;δ为Dirac Delta函数。
1.1 流体单元的受力分析
截取一段流体单元dx为受力分析对象,流体单元受离心力、科氏力、惯性力、压力和管内壁对流体的作用力,其受力如图2所示。
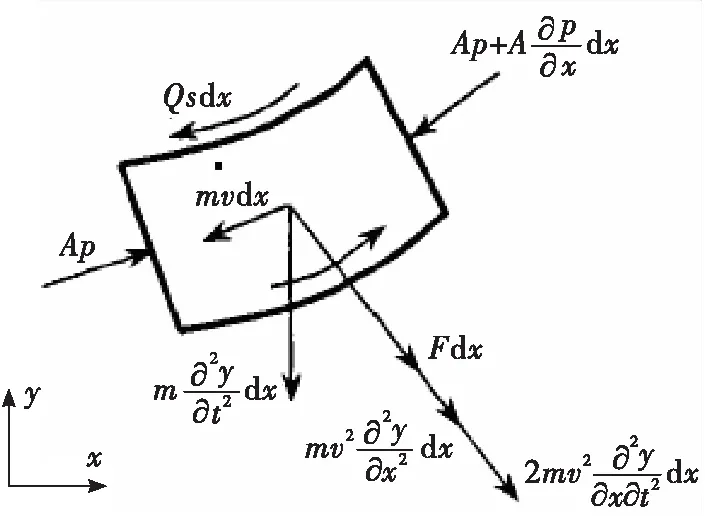
图2 流体单元受力分析Fig.2 Forces acting on the fluid element
可分别列出x、y方向的力平衡
(2)
式中:y为管路横向位移;θ为y对x坐标值的导数角;m为单位长度流体质量;v为流体流速;p为单位面积流体压力;s为管路截面内径周长;F为管内臂作用流体法向力;Q为管壁作用流体切向力;A为通流截面面积。
1.2 管路单元的受力分析
截取一段管路单元dx为受力分析对象,管路单元受剪力、轴力、弯矩、惯性力和流体作用管内壁力,其受力图3所示。
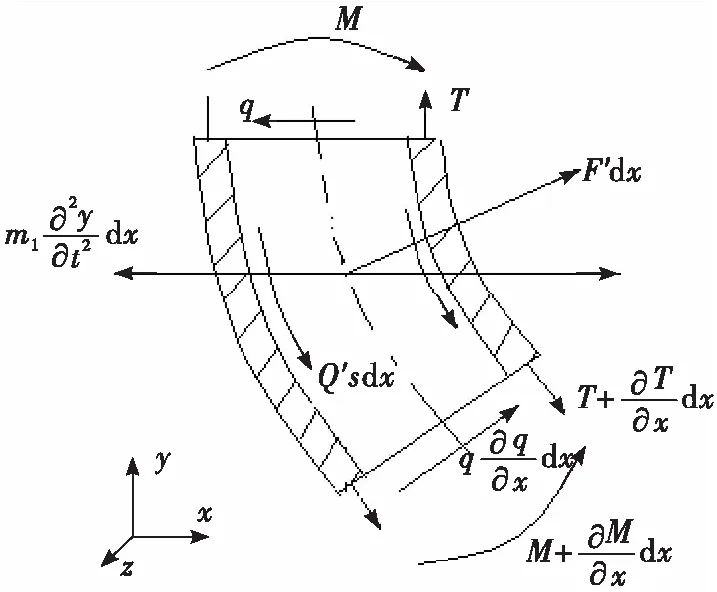
图3 管路单元受力分析Fig.3 Forces acting on the pipe element
考虑管路端面的非线性弹簧反力,x、y方向的力平衡方程和z方向力矩平衡方程
(3)
式中:y为管路横向位移;θ为y对x坐标值的导数角;m1为单位长度管路质量;q为管路截面剪力;M为管路截面弯矩;T为管路截面轴力;F′为流体对单位长度管臂法向力;Q′为流体对管壁切向力;l为管路长度;δ为Dirac Delta函数。
1.3 管路运动微分方程
为对管路非线性振动特征分析,将管路材料设为Kelvin—Voigt型材料,a为材料黏弹性系数,其应力—应变关系为
(4)
根据材料力学,由式(4)可得
(5)
(6)
管路振型一般有简支振型、固支振型和悬臂振型,管路分析理论模型一端为固定约束,另一端为非线性弹簧位移约束,选取管路前三阶悬臂振型函数对方程(6)求解,悬臂梁振型函数为
(7)
式中:l为管路长度;β1、β2、β3为悬臂管路振型参数,悬臂梁的第一阶振型β1为1.875/l,第二阶振型β2为4.694/l,第三阶振型β3为7.855/l。
对式(6)按前三阶振型函数加权之和积分获得离散化运动方程
(8)

2 燃油管路的振动稳定分析
姿控发动机的燃料输送管路材料为不锈钢(1Cr18Ni9Ti),管路模型参数如:管长为600 mm,直径为18 mm,管子壁厚为1.5 mm,流体密度为850 kg/m3,管路黏性系数设为a=0.02,非线性刚度系数设为k1=10 N/mm、k2=1.2 N/mm。采用四阶Runge—Kutta法对式(8)计算,计算时间步骤Δt=0.000 55 s,计算次数为7 000。
2.1 燃料管路的稳定特征线分析
管路稳定特征线表示管路稳定临界流量与开启、关闭时长的关系曲线。按电磁阀开启时长、关闭时长与流量参数计算管路稳定特征线如图4和图5所示。

图4 电磁阀开启时长对管路稳定特征线的影响Fig.4 Effect of the opening time of the solenoid valve steady characteristics line of pipeline
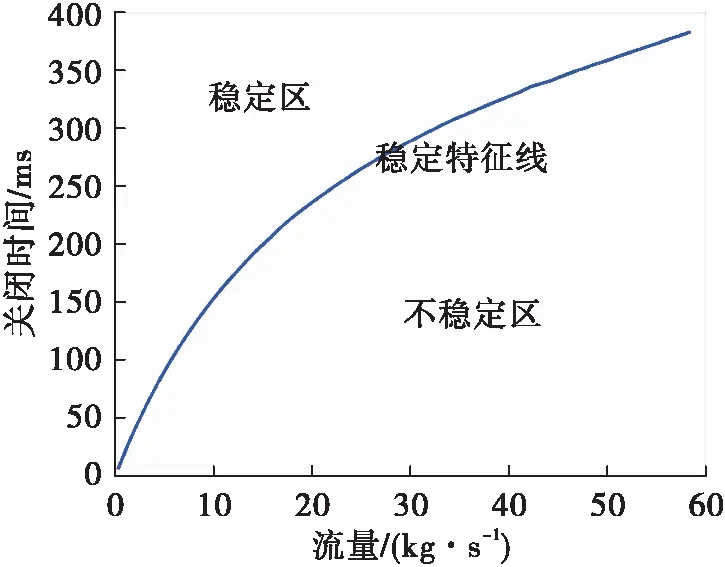
图5 电磁阀关闭时长对管路稳定特征线的影响Fig.5 Effect of the closing time of the solenoid valve on steady characteristics line of pipeline
分析可知,电磁阀开启时长、关闭时长均随着管路燃料稳定临界流量的增加而增加,且在某一定稳定临界流量(20~30 kg/min)下,关闭时长约为开启时长的4~5倍。沿特征线可将管路振动分为稳定振动区和不稳定振动区(位于特征线下方区域为不稳定区域,而位于特征线上方区域为稳定区域)。在某一稳定临界流量下,当电磁阀开启、关闭时长处在不稳定区内时,燃料管路将产生不稳动振动。
2.2 电磁阀开启时长对管路振动的影响
2.2.1 管路振动稳定分析
当电磁阀开启时长位于稳定区时,分析不同电磁阀开启时长、不同流量(30 kg/min和50 kg/min)对管路中心点位移响应曲线的影响规律,计算结果如图6~图7所示。

图6 流量30 kg/min时不同开启时长的管路位移时域曲线Fig.6 Displacement curve of pipe with different opening time when the flow rate is 30 kg/min
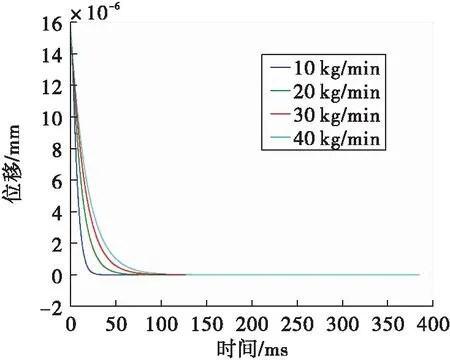
图7 开启时长100 ms时不同流量的管路位移时域曲线Fig.7 Displacement curve of pipe with different flow rate when the opening time is 100 ms
由图6和图7分析可知,电磁阀开启时长处于稳定振动区时,仿真得到的管路位移值均迅速衰减到零。其中,当燃料流量一定时,管路位移衰减到零的时间随着电磁阀开始时长增加而减小,呈负相关关系;当电磁阀开启时长一定时,管路位移衰减到零的时间随着管路流量的增加而增加,呈正相关关系。其原因在于电磁阀开启时长、管路流量均是影响管路阻尼比的主要参数,当电磁阀开启时长达到特征线时,管路的阻尼比最大。
2.2.2 管路动态扩张失稳分析
在管路失稳区分析中,对同一流量不同电磁阀开启时间、同一电磁阀开启时长不同流量两种情况下的管路非线性振动进行仿真计算。管路中心点位移响应曲线如图8和图9所示。
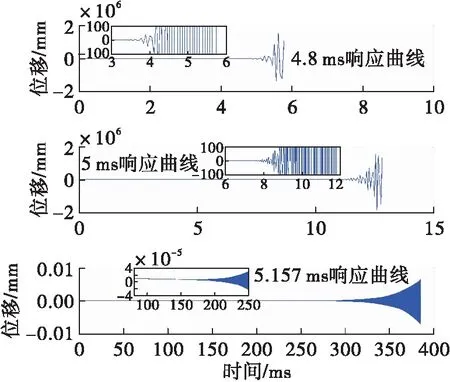
图8 流量30 kg/min时不同开启时长对管路位移的影响Fig.8 Displacement curve of pipe with different opening time when the flow rate is 30 kg/min

图9 开启时长5.157 ms时不同流速对管路位移的影响Fig.9 Displacement curve of pipe with different flow rate when the opening time is 5.157 ms
由以图8和图9分析可知,在同样流量下,随着电磁阀开启时长增加管路的振动频率也随之增加,呈正相关关系;在相同电磁阀开启时长下,随管路流量增加,管路的振动频率随之减小,呈负相关关系。当电磁阀开启时长值或管路燃料流量值靠近特征线时,管路振动位移扩张起始时间变长但位移扩张率降低,反之亦然。其中,燃料流速增加导致管路振动位移扩张迅速增大,如流量从30 kg/min增大到32 kg/min时,管路振动位移呈几何量级增加。由此可见,燃油流速增大是影响管路振动扩张断裂的主要因素。
2.3 电磁阀关闭时长对管路振动的影响
2.3.1 管路稳定分析
当电磁阀关闭时长位于稳定区或特征线上时,分析不同电磁阀关闭时长、不同流量对管路中心点位移响应曲线的影响规律,计算结果如图10~图12所示。不同流量时管路振动频率如图13所示。
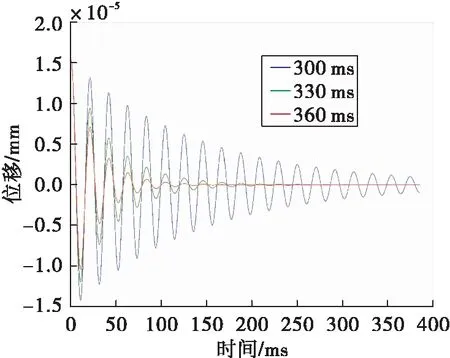
图10 流量30 kg/min时不同关闭时长对应的管路位移曲线Fig.10 Displacement curve of pipe with different closing time when the flow rate is 30 kg/min

图11 关闭时长300 ms时不同流量对应管路位移曲线Fig.11 Displacement curve of pipe with different flow rate when the closing time is 300 ms

图12 关闭时长245 ms且流量为20 kg/min时管路位移曲线Fig.12 Displacement curve of pipe when the closing time is 245 ms and the flow rate is 20 kg/min

图13 不同流量时管路的振动频率Fig.13 Vibration frequency of pipe at different flow rate
由以上分析可知,同一流量下,随着电磁阀关闭时长增加,管路中心点位移在较短周期内迅速衰减到零,管路振动消除;同一电磁阀关闭时长时,随着管路燃料流速的降低,管路中心点位移在较短周期内迅速衰减至零,管路振动消除。当电磁阀关闭时,燃料流速是逐渐降低的,相当于降低了管路的总刚度,使得管路振动频率范围较低,约为45~60 Hz。然而,当电磁阀关闭时长处于特征线时,管路位移按单频等幅振动方式持续振动,且管路振动频率随流量的增加而增加。
2.3.2 管路周期扩张失稳分析
在管路失稳区分析中,对同一流量不同电磁阀关闭时间、同一电磁阀关闭时长不同流量两种情况下的管路非线性振动进行仿真计算。管路中心点位移响应曲线如图14~图15所示。

图14 流量50 kg/min时不同关闭时长对应的管路位移曲线Fig.14 Displacement curve of pipe with different closing time when the flow rate is 50 kg/min

图15 关闭时间300 ms时不同流量对应的管路位移曲线Fig.15 Displacement curve of pipe with different flow ratewhen the closing time is 300 ms
由以上分析可知,同一燃油流量时,管路振动位移随着电磁阀关闭时长的增加急剧降低,但管路位移振动初始时间提前;同一电磁阀关闭时长时,管路振动位移随燃油流速的增加呈几何级数增加,但管路位移振动初始时间变长。因此,当流量参数、电磁阀关闭时长处于不稳定区域时,快速关闭电磁阀将引起管路较大的扩张位移,可能导致管路断裂。
3 结论
论文建立了燃油管路的非线性液固耦合非线性振动模型,采用加权余量法和四阶Runge—Kutta法对该模型进行了数值仿真,分析了电磁阀开启时长、关闭时长造成的燃油瞬变流速对燃料管路的非线性振动影响,获得了燃油管路在瞬变流速激励下的振动特性。
1)电磁阀开启、关闭时长均随着管路燃料稳定临界流量的增加而增加,且在某一定稳定临界流量下,关闭时长约为开启时长的4~5倍。沿特征线可将管路振动分为稳定振动区和不稳定振动区(位于特征线下方区域为不稳定区域,而位于特征线上方区域为稳定区域)。
2)电磁阀开启时长处于稳定区域或特征线上时,管路位移均迅速衰减到零。在管路失稳区分析时,管路振动频率与电磁阀开启时长呈正相关关系,与管路燃油流量呈负相关关系。燃油流速增大是影响管路振动扩张断裂的主要因素,且燃料瞬变流速引起的燃料管路振动形式为多频率、变幅值的扩张振动。
3)电磁阀关闭时长处于稳定区域分析或特征线上时,燃油瞬变流速引起的管路位移在较短周期内迅速衰减到零,或产生较小的单频等幅振动,但管路振动位移均极小。在管路失稳区分析时,快速关闭电磁阀将引起管路产生较大的单频、幅值扩张位移,可能导致管路断裂。
