基于演化博弈模型的矿区环境治理及监管策略分析

曾繁伟 , 石夫磊

(1.山东工商学院 工程学院,山东 烟台 264005;2.首都经济贸易大学 信息学院，北京 丰台 100070)

煤炭资源在我国的能源结构中占有相当大的比重，是国民经济稳定发展的能源基础，但是，煤炭资源的开采过程也伴随着十分严重的生态环境污染问题，比如大气污染、固体废弃物污染、水污染以及其他污染等。严重污染的背后，即与煤炭企业开采过程有关，也与地方政府的治理力度息息相关。近年来，政府高度重视矿区环境的保护，相继颁布了与矿区环境保护直接相关的法律法规13项，加快与促进了矿区环境保护的进程，但是，在矿区环境治理的过程中，依然存在制度上的不完善、监管不严等问题，矿区环境的治理与监管问题依然是一个亟待解决的问题。

近年来，已有部分学者采用不同的方法对矿区环境问题进行了深入研究，比如王志宏、何志强[1]对矿区环境的可持续发展结构模式进行了探讨，进而剖析了实现该结构模式的历史演变过程，并对该模式下的存续性以及稳定性进行了分析；孙玉峰[2]将矿区环境视为一个大的系统，并将其分为固体废物、水以及大气3个子系统，构建了基于矿区环境的系统动力学模型，并以某矿区为例进行了历史模拟与动态仿真；李宝旭、卢国斌[3]采用模糊数学的方法，构建了矿区环境质量综合评价的模糊数学模型；周玉民、卢国斌[4]对矿区环境系统的结构以及模型进行了深入探讨，并构建了包含环境污染模型以及环境保护模型的矿区环境系统模型，并应用环境质量分析方法对矿区环境的质量问题作了深入分析。

演化博弈论的方法区别于传统的博弈论理论，其以有限理性作为假设条件，最早由Smith和Price提出，以演化稳定策略(ESS)及复制动态方程广为应用[5-7]。将演化博弈论的方法应用于环境问题已经成为近年来的热点，比如将演化博弈论方法应用于大气污染、雾霾问题[8-10]；环境规制下企业与政府策略之间的博弈行为分析[11-15]等，现有的研究主要考察在博弈双方的演化过程中均衡点的稳定性以及是否存在演化稳定策略等[9-15]，而忽略了对于中心点的深入探讨。

本文在借鉴前人研究的基础上，贡献在于：结合矿区环境治理特点，将演化博弈论的方法应用于矿区环境的治理问题中，构建煤炭企业与地方政府之间的演化博弈模型，探讨煤炭企业与地方政府之间的系统演化过程；分析了博弈双方在均衡点的稳定性，并重点对中心点的演化过程进行了探讨；在不同参数调整下对中心点状态的演化博弈过程进行了仿真分析。

1煤炭企业排污与地方政府监管行为演化博弈模型构建与分析

1.1 模型条件假设与符号说明

在煤炭矿区环境污染的治理过程中，煤炭企业在选择贯彻地方政府的环境政策的同时，也在不断地追求自己企业本身的利益最大化，煤炭企业与地方政府之间的博弈行为表现为动态的重复博弈。

本文从演化博弈的角度来分析煤炭企业的排污行为与地方政府的监管策略在利益冲突下如何做出最优的行为决策，在构建煤炭企业与地方政府博弈双方的演化博弈模型之前，提出如下假设：

假设1：矿区环境污染问题存在很多影响因素，比如大气污染、固体废弃物污染、水污染以及其他污染等，为使问题描述方便，在此合理假设矿区环境质量的高低皆由煤炭企业的“排污”行为所致，且将其分为“合规排污”与“非法排污”两种情况。

假设2：博弈过程的参与者只有2个，一是地方政府监管机构D，二是煤炭企业M，两者之间存在博弈行为，并且博弈的双方都是有限理性的。

假设3：博弈主体D和M只有两种策略。地方政府监管机构选择“监管”或“不监管”，其策略集合为(监管D1，不监管D2)，煤炭企业可供选择的也有2种策略，一是“合规排污”，即在规定排放标准允许的范围内合理排放污染物，二是“非法排污”，其策略集合为(合规排污M1，非法排污M2)，此种情况下，煤炭企业在利益的驱使下，将会忽略污染物排放的相关规定，从而造成污染物的排放严重超标，进而影响矿区的生态环境。

假设4：煤炭企业选择“合规排污”策略的概率为x(0≤x≤1)，则其选择“非法排污”策略的概率为1-x；地方政府监管机构选择“积极监管”策略的概率为y(0≤y≤1)，则其选择“消极监管”行为策略的概率为1-y。

假设5：政府会给煤炭企业制定一个排污标准S(S≥0)，当煤炭企业的排污量小于S，即煤炭企业合规排污时，煤炭企业与地方政府监管机构收益皆为0，设煤炭企业“非法排污量”为S1(S1>S)，政府会对煤炭企业超标的排污量进行处罚，设α(α>0)表示每单位的超标量进行的处罚金额，当煤炭企业进行非法排污时，其需要支付α(S1-S)。

假设6：当企业进行非法排污时，其会获得额外收益V(V>0)。当煤炭企业合规排污时，如果地方政府采取不监管的策略，则其收益为0，同时，不需要支付监管成本。

假设7：当煤炭企业非法排污时，如果地方政府采取不监管的策略，此时，上级政府对地方政府的不作为处罚为-R，(R≥0)，当煤炭企业进行非法排污，同时地方政府采取监管策略时，上级政府对地方政府会有一个正面评价R1(R1>0)，同时，当地方政府采取监管策略时，其需要付出的监管成本为C(C>0)。

假设8：当地方政府采取监管策略时，可以及时发现煤炭企业的“非法排污”行为。当地方政府采取“不监管”策略时，不能发现煤炭企业的“非法排污”行为。

由上述假设条件，可以得到博弈双方的支付矩阵如表1所示。

1.2 博弈双方演化博弈模型建立

(1)

联立上述3个方程可以求得煤炭企业的演化博弈复制动态方程[16-17]为：

(2)

(3)

联立上述3个方程可以求得地方政府监管机构的演化博弈复制动态方程为：

(4)

则由博弈双方(2)、(4)组成的演化动态系统的复制动态方程如式(5)所示：

(5)

1.3 博弈双方演化博弈稳定性分析

根据雅可比矩阵局部渐进稳定性的分析方法，可以求得复制动态系统在均衡点的演化稳定性，对复制动态系统的偏微分方程分别求偏导，设该系统雅可比矩阵为J，可以计算出该系统的雅可比矩阵如下所示：

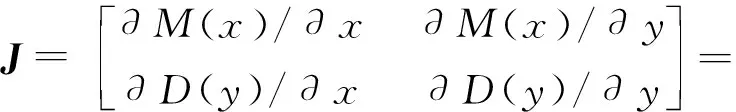
(6)

设该矩阵的行列式为detJ，该矩阵的迹为trJ，为使公式描述更加简明，设

(7)

则

detJ=∑1∑4-∑2∑3

(8)

trJ=∑1+∑4

(9)

在复制动态系统(5)中，令M(x)=0，D(y)=0，可以求得可能存在的均衡点为E1(0，0)，E2(0，1)，E3(1，0)，E4(1，1)，E5(x*，y*)，其中：

(10)

根据公式(8)，(9)，带入均衡点的数值，可以得到矩阵行列式以及矩阵的迹的表达式如下所示：

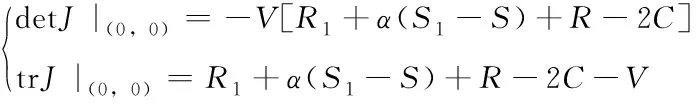
(11)

(12)

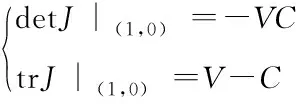
(13)

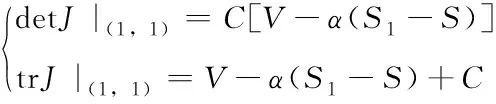
(14)

联立方程式(11)～(14)，可得：

(15)

根据演化博弈理论可知，如果满足detJ>0且trJ<0，则对应的均衡点即为局部渐进稳定不动点，其对应的演化策略即为演化稳定策略。为便于分析，设：

(16)

定义1：若ζ1>0，则必有ζ3>0；若ζ3<0，则必有ζ1<0。

证明：若ζ1>0，则R1+α(S1-S)+R-2C>0，即R1+α(S1-S)+R>2C，此时，一定存在ζ3=R1+α(S1-S)+R-C>2C-C=C，又C>0，故ζ3>0。同理，若ζ3<0，则必有ζ1<0。

由以上分析，可以将其分为以下几种情形：

情形1：ζ1>0，ζ2>0。此时，系统均衡点稳定性分析如表2所示。在此条件下，存在2个鞍点，1个不稳点以及1个中心点，E1(0，1)为该系统演化均衡稳定点，此时，企业选择“非法排污”策略，地方政府监管机构选择“监管”策略。

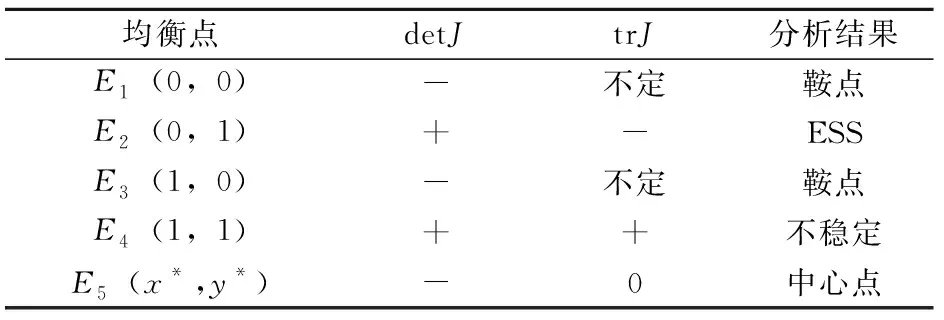
表2 均衡点稳定性分析(情形1)

情形2：ζ1>0，ζ2<0。此时，系统均衡点稳定性分析如表3所示。在此条件下，存在4个鞍点以及1个中心点，此时，没有均衡的稳定点存在。

表3 均衡点稳定性分析(情形2)

情形3：ζ3<0，ζ2>0。此时，系统均衡点稳定性分析如表4所示。在此条件下，存在2个鞍点、1个不稳定点以及1个中心点，E1(0，0)为该系统演化均衡稳定点，此时，企业选择“非法排污”策略，地方政府监管机构选择“不监管”策略。

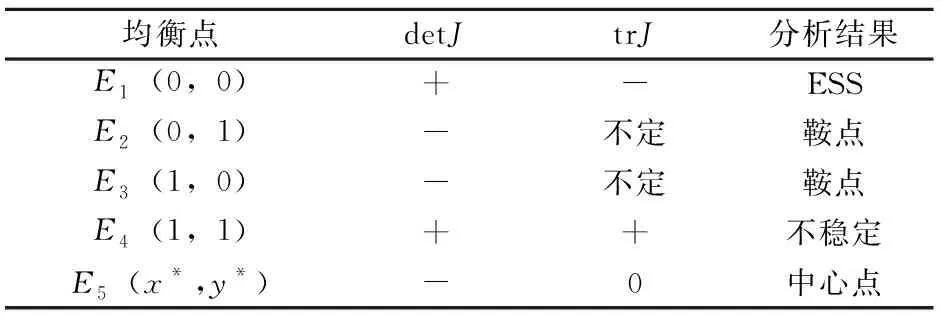
表4 均衡点稳定性分析(情形3)

情形4：ζ3<0，ζ2<0。此时，系统均衡点稳定性分析如表5所示。在此条件下，存在3个鞍点以及1个中心点，E1(0，0)为该系统演化均衡稳定点，此时，企业选择“非法排污”策略，地方政府监管机构选择“不监管”策略。

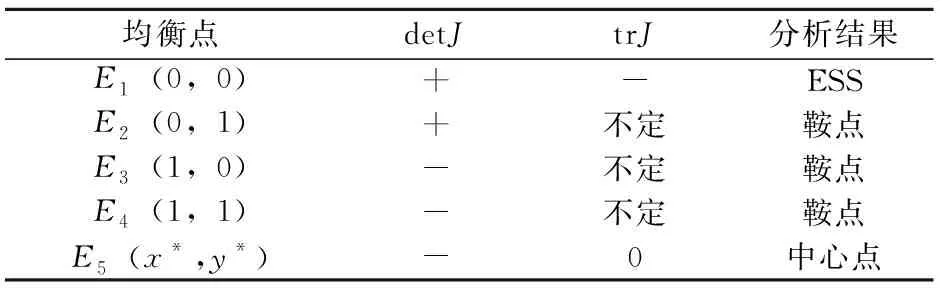
表5 均衡点稳定性分析(情形4)

上述4种情形对应的相位图如图1～4所示。

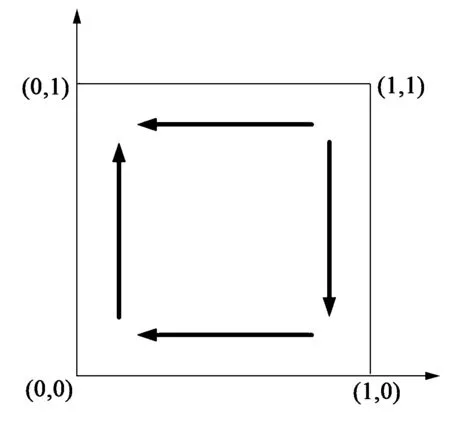
图1 情形1系统演化相位图

图2 情形2系统演化相位图

图3 情形3系统演化相位图

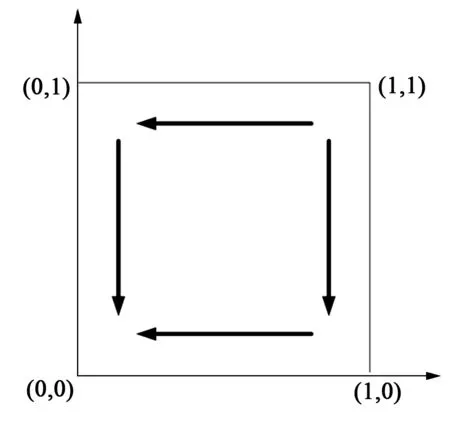
图4 情形4系统演化相位图

为了更加直观展示其演化过程，需要对其进行数值仿真分析。

1.4 数值仿真分析

1.4.1 4种情形下系统演化状态

为了进一步直观地研究博弈双方系统演化的影响因素，求解微分方程，根据数值方法判定系统博弈双方的演化趋势：在满足情形1，2，3，4条件的基础上，对复制动态方程中参数进行设定，如表6所示。

表6 复制动态方程参数设定

4种情形对应的模拟仿真演化趋势见图5。

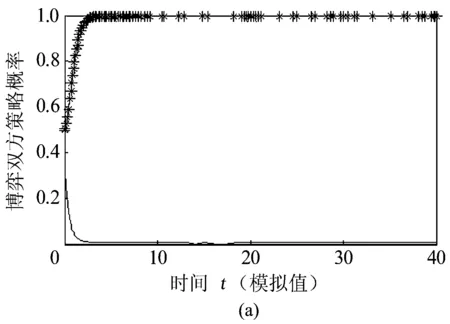
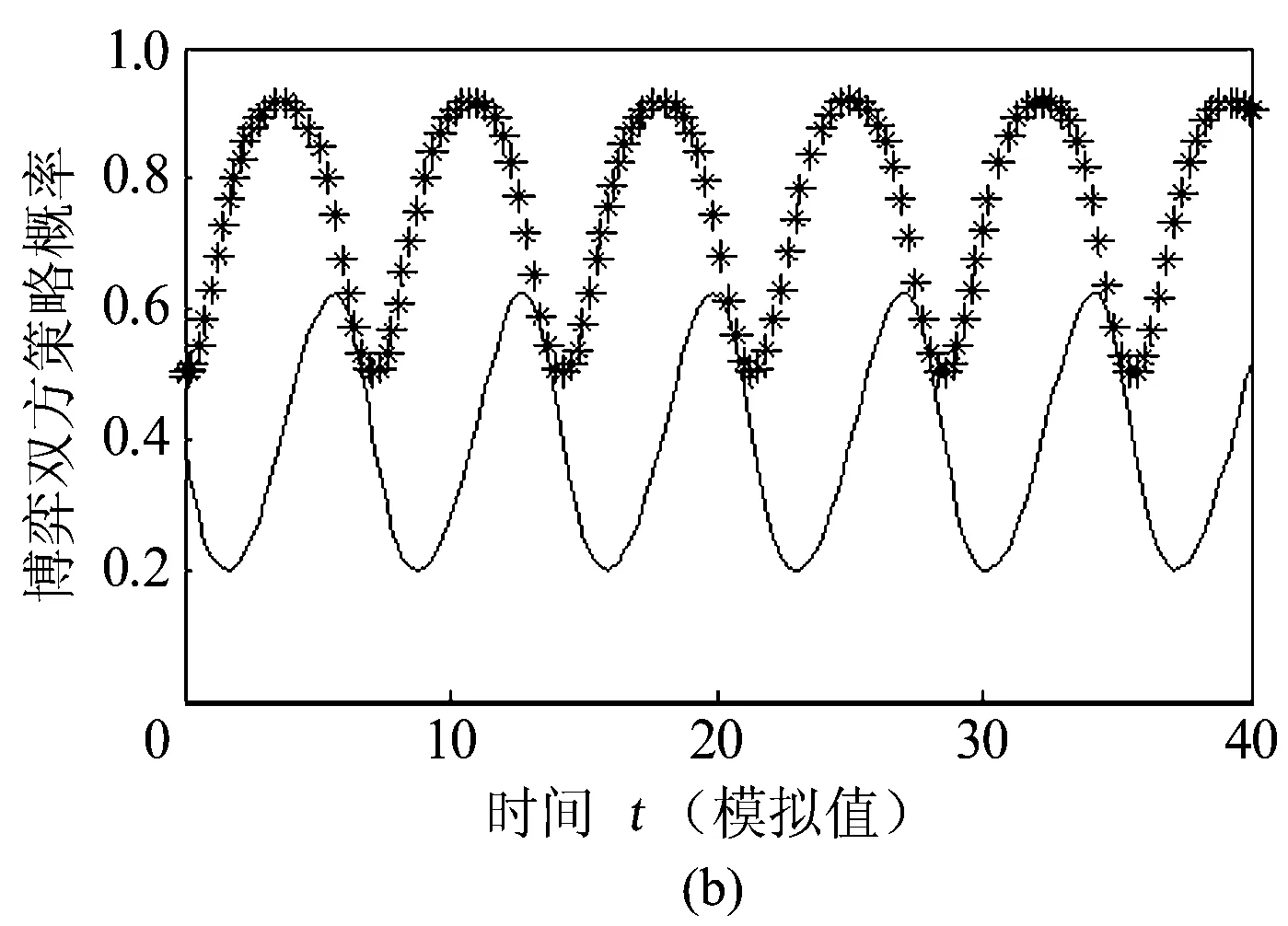
煤炭企业排污(**)；地方政府监管(——)图5 4种情形下对应的系统模拟仿真演化趋势

在上述4种情形中，从图中可以看出，情形2不存在稳定的系统演化过程，煤炭企业与地方政府的系统演化过程周期震荡，没有稳定的均衡状态，主要是由于演化双方付出的成本、收益以及奖惩政策的不定性，系统演化过程很难达到稳定的状态，系统双方采取的策略因而也是不确定的；情形1，3，4存在稳定的演化均衡点，在情形1中，如果煤炭企业选择“非法排污”，地方政府便顺其自然，选择“监管”策略，情形1，2与现实情况是比较符合的。然而在情形3，4中，煤炭企业均选择“非法排污”，地方政府却选择“不监管”策略，此种情形往往不可能发生。

1.4.2 情形2参数变化时系统演化状态变化

在上面的分析中可知，情形2不存在稳定的演化过程，煤炭企业与地方政府的策略变化是不确定的，下面考察在满足情形2条件的基础上当参数发生变化时系统的演化改变。分别对参数调整如下：

参数调整1：在其他数值不变的情况下，将R由原来的2增大到10，即增大上级政府对地方政府的不作为处罚。

参数调整2：在其他数值不变的情况下，将C由原来的3缩小到1，即缩小地方政府对煤炭企业排污的监管成本。

参数调整3：在其他数值不变的情况下，将S由原来的10缩小到2，即缩小地方政府给煤炭企业制定的排污量标准。

当参数调整后，情形2系统演化过程以及3种参数调整后的演化趋势如图6所示。

煤炭企业排污(**)；地方政府监管(——)图6 情形2系统演化过程以及3种参数调整后的演化趋势

从图6可以看出，在增大上级政府对地方政府的不作为处罚时，相对于情形2，此时地方政府选择监管的概率明显上升，在一定的时期内，煤炭企业选择“非法排污”的概率大大降低。在缩小地方政府对煤炭企业排污的监管成本时，地方政府选择“监管”策略的概率明显增大，并且监管的周期变得更长。缩小地方政府给煤炭企业制定的排污量标准时，地方政府选择“监管”的概率大大提高，并且周期变得更短，说明地方政府选择“监管”的频率大大提高。

2 结 论

基于演化博弈模型，系统考察了煤炭企业的排污行为与地方政府监管之间的策略的演化过程，求得了不同情形下系统博弈双方的均衡点，并对均衡点的稳定性进行了分析。研究表明，该系统的演化过程存在4种情形，情形1，2较能代表现实情况，进一步，对中心点位置的演化稳定性做了详细探讨，在增大上级政府对地方政府的不作为处罚时，相对于情形2，此时地方政府选择监管的概率明显上升，在一定的时期内，煤炭企业选择“非法排污”的概率大大降低。在降低地方政府对煤炭企业排污的监管成本时，地方政府选择“监管”策略的概率明显增大，并且监管的周期变得更长。缩小地方政府给煤炭企业制定的排污量标准时，地方政府选择“监管”的概率大大提高，并且周期变得更短，说明地方政府选择“监管”的频率大大提高。

矿区环境的治理，必然离不开地方政府的合理监管以及煤炭企业的努力，本文基于上述的分析结果，给出如下一些建议：

对地方政府的不作为行为，上级政府要对其进行严厉地处罚，制定合理的煤炭企业排污标准，加大对矿区环境保护的监管力度，尽快出台更加具有针对性、体系更加严密的矿区环境保护政策，降低地方政府对矿区环境监管的成本。对于煤炭企业来说，要自觉加大环境保护的责任意识，积极进行技术革新，降低煤炭开采排污量，积极配合政府的监管行为等。

由于上述演化过程是在数值仿真的条件下进行的，尚存在一些不足之处，下一步可以考虑使用更加真实的数据进行研究。