基于计算运动学的掩护式液压支架运动特性研究
2018-09-17许永祥张金虎张德生
许永祥,张金虎,佟 友,张德生
(1.煤炭科学研究总院 开采研究分院,北京100013;2.天地科技股份有限公司 开采设计事业部,北京100013;3.煤炭资源高效开采与洁净利用国家重点实验室(煤炭科学研究总院),北京 100013)
液压支架是煤矿长壁综采工作面的“钢铁长城”,是长壁机械化采煤的关键装备,为采煤工作面各个工序安全高效运行提供作业空间和坚实的安全保障。合理的液压支架设计能使支架与围岩实现理想的耦合关系,增强支架对围岩的适应性。传统的液压支架结构设计通常采用传统的运动学方法[1-10],即解析法和图解法。但其主要依赖于系统的几何拓扑关系,因而仅适用于含刚体和关节数目较少的系统的研究,对于复杂系统其所建立的方程较为复杂,求解不方便。且通常只求解出支架结构间的位置关系,而未对支架结构运动中的速度和加速度进行求解。本文基于计算运动学,通过约束方程建立液压支架结构件间的运动学方程,求解液压支架在不同工作状态的姿态、位置、速度和加速度关系,有利于液压支架的结构设计、分析优化、质量监测、智能控制以及与采场围岩的耦合状态等[11-15]。
1 计算运动学简介
运动学分析的目的在于根据已知的输入运动,来确定目标的位置、速度和加速度,求解系统运动关系可以确定系统的状态。完整的机械系统运动学分析包含3个阶段:位置分析,速度分析和加速度分析。通常来说,系统坐标的运动学关系是非线性的,因而求解过程需要使用迭代数值程序(如牛顿-拉普森法)。位移方程的一次、二次微分可得相应的速度运动方程和加速度运动方程,由此可得出一系列的以速度和加速度表示的线性代数方程。
计算运动学基于刚体结构假设,即:假设多结构系统由刚体组成,结构自身变形可以忽略。刚体分析中,结构中任意两点间的距离保持不变。如果结构仅仅发生小变形且小变形在整体运动过程中可以忽略,则该结构可以认为是刚体结构。如果研究的内容在于应力或者结构发生大变形且大变形的影响不可忽略,则刚体假设不再适用,需采用变形体模型来处理。
计算运动学方法可以用于求解包含刚体和关节数多的系统。该方法建立了坐标间代数运动约束关系方程,这些约束方程通常为坐标的非线性函数,可以采用迭代数值计算方法来确定系统中刚体的位置。通过约束方程关于时间的一次和两次微分可以分别获得以速度和加速度表示的线性系统方程。这些线性方程可以直接求解得到坐标的一次和二次时间导数。
2 液压支架运动学方程的建立
计算运动学中,刚体位移可以通过一个参考点的平移和通过该参考点的旋转组成。可以使用非线性三角函数来确定机构中所有刚体的位置和方向。计算运动学方程由结构间的约束方程组成,约束方程通常包含:固定约束、转动关节约束、平动关节约束和驱动约束方程。计算运动学使用局部坐标向全局坐标转换的方法,摆脱对结构几何拓扑关系的依赖,将复杂的问题简单化,便于建立复杂结构关系的数学模型。
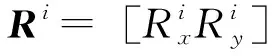
(1)

(2)
一个包含nb个刚体的多体系统具有3×nb个独立广义坐标,用矢量q表示为

(3)
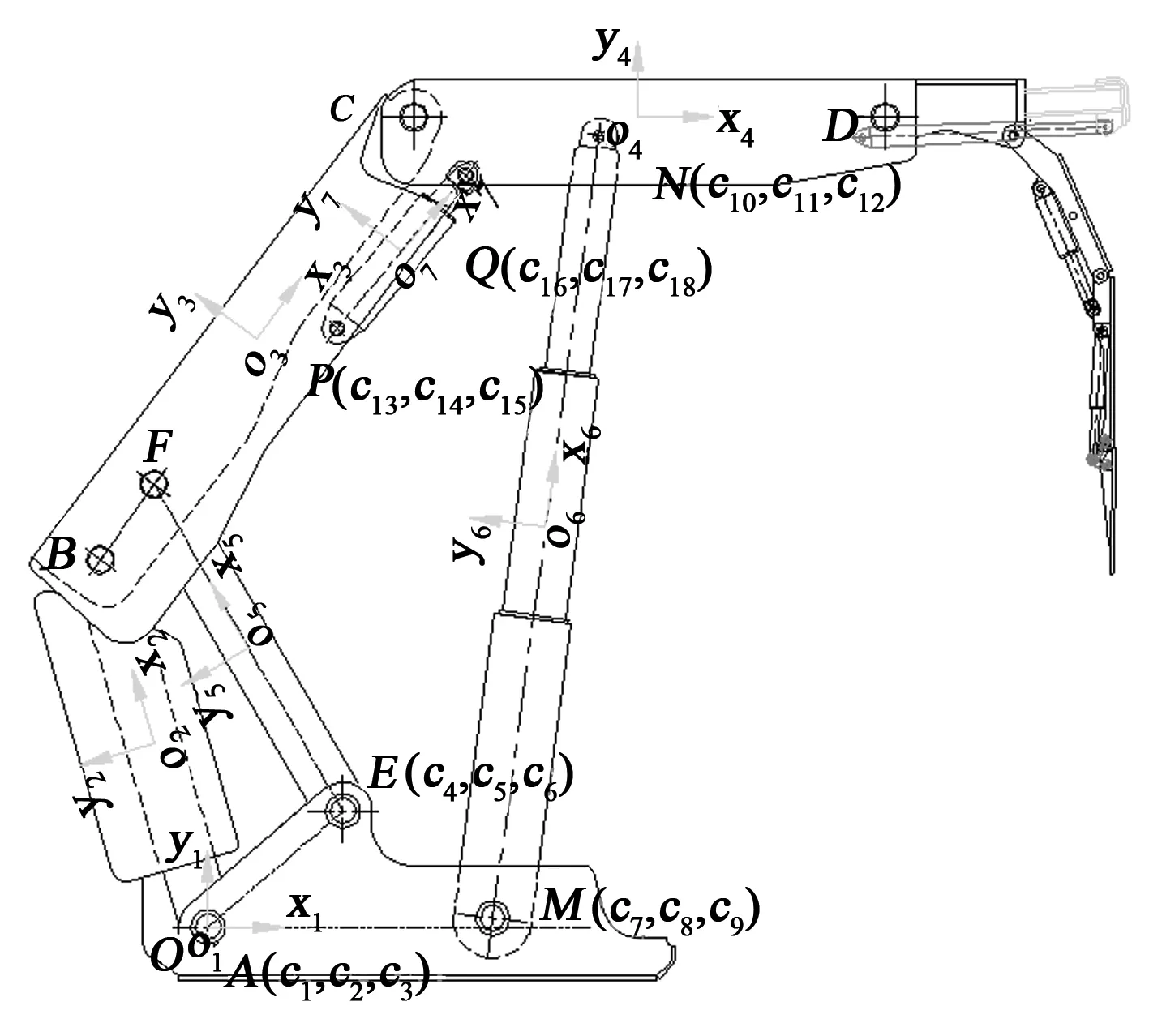
图1 液压支架模型
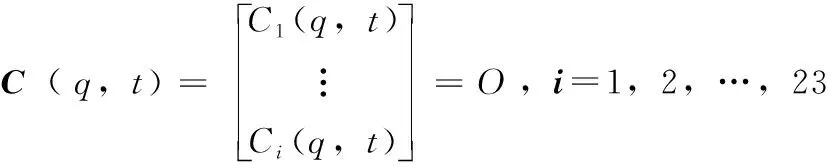
(4)
(5)
(6)
C3(q,t)=θ1-c3
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
C22(q,t)=f(t)
(26)
C23(q,t)=g(t)
(27)
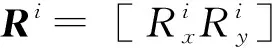
3 液压支架约束矩阵求解
系统坐标的运动学约束方程关系是非线性的,因而需要使用迭代数值法求解(如牛顿-拉普森法)。Matlab软件在非线性矩阵方程组求解方面有着成熟的求解程序,可直接调用已有库函数进行求解,十分方便。通过调节支架立柱和平衡千斤顶的长度,可以显示出支架不同的工作姿态。图2(a)为支架顶梁“抬头”、“低头”姿态,图2(b)为顶梁保持水平状态不同支护高度时支架的工作姿态。
3.1 顶梁前端运动轨迹、支架立柱和平衡千斤顶的伸缩量的关系
液压支架顶梁前端的运动轨迹是液压支架设计时需要考虑的重点,对于液压支架自身和工作面顶板与煤壁的稳定性都有影响。由于四连杆机构的约束,支架顶梁保持水平状态下,支架顶梁前端的运动轨迹为S型双纽线(图3),合理的四连杆参数可使顶梁在液压支架工作高度段(4000~5500 mm)内顶梁摆动较小,且在液压支架降架过程中顶梁向煤壁侧运动,使得液压支架在顶板来压时保持自身稳定,同时施加给顶板和煤壁以指向煤壁的水平作用力,可防止工作面顶板端面冒顶和煤壁片帮,提高液压支架抗水平载荷能力[1,9-10]。
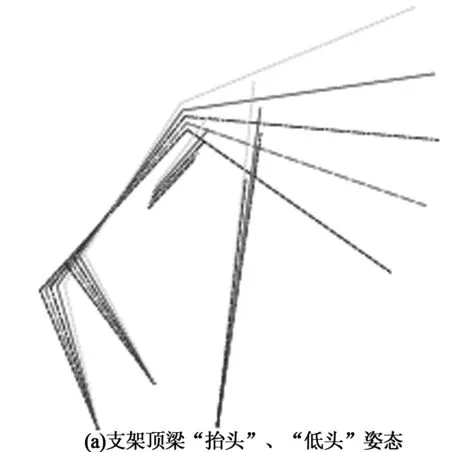

图2 支架姿态求解简图

图3 液压支架顶梁前端点运动轨迹线
3.2 液压支架立柱和平衡千斤顶的伸缩量的关系
掩护式液压支架的立柱是主要的支撑体和承载体,控制着液压支架的高度,承载着上覆岩层的压力。掩护式液压支架的平衡千斤顶铰接于支架顶梁和掩护梁之间,可以调节顶梁的倾角、合力及合力作用点位置,对液压支架姿态调节和稳定性控制有着至关重要的作用[16]。对于掩护式液压支架的控制主要是通过立柱和平衡千斤顶的伸缩量来实现,掌握它们的伸缩量与支架整体姿态和受力特征是实现液压支架自动化、智能化的基础。图4所示为支架顶梁保持水平情况下,立柱长度和平衡千斤顶长度关系。
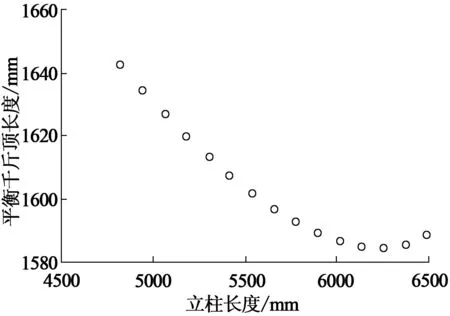
图4 立柱长度和平衡千斤顶长度关系
4 结束语
采用计算运动学方法建立液压支架运动学约束方程不必考虑复杂结构的几何拓扑关系,采用Matlab已有的库函数进行非线性方程组求解,降低计算难度,与传统支架设计中采用解析法和画图法相比,效率大大提高。同时,建立的运动约束方程用别的计算机语言编写也较为容易,可用于液压支架质量监测、智能控制等方面。
