合肥地区膨胀土残余强度的试验研究

赵明华，蒋晓庆

(1.安徽广播电视大学 马鞍山分校,安徽 马鞍山 243000；2.安徽广播电视大学 开放学院,合肥 230022)

一、引言

实际工程中，膨胀土边坡设计是按照膨胀土饱和峰值强度计算的，但是结果证明，膨胀土边坡还是会发生滑动。近年来，不少学者认为膨胀土边坡设计应以膨胀土残余强度计算，因为膨胀土边坡的变形破坏演变是边坡土体的抗剪强度由峰值向残余值逐渐衰减的过程。刘特洪提出采用残余强度等于给予膨胀土或层间软弱面一定的强度储备，工程实践的结果赋予了膨胀土力学属性的深化[1]。吴珺华等通过FLAC3D数值模拟分析，结合强度折减法，计算出膨胀土的残余强度对膨胀土边坡稳定性有影响[2]。刘华强通过裂缝对膨胀土抗剪强度指标影响的试验，得出膨胀土残余强度和膨胀土多次干湿循环后的强度指标接近[3]。

为了深入分析膨胀土残余强度特性，很多学者对其影响因素展开了大量的研究。李新民通过工程包边法，分析了干湿循环前后膨胀土残余强度的变化，提出干湿循环后膨胀土残余强度降低[4]。肖杰等通过对南宁膨胀土进行残余强度试验，提出初始干密度对残余强度影响不大，低应力影响显著[5]。左巍然等通过对宁明灰白膨胀土进行残余强度试验分析，提出残余强度与它的物质组成和颗粒相关[6]。张晓丽通过室内直剪试验分析了饱和后膨胀土的残余强度明显低于非饱和状态的残余强度[7]。

鉴于大量的文献调研，关于不同初始含水率、不同竖向应力对膨胀土残余强度影响的研究文献不多。孟庆宇通过室内快剪试验，提出不同初始含水率在较小应力(100kPa、200kPa)作用下，膨胀土残余强度相差不大；在较大应力(300kPa、400kPa)作用下，随着初始含水率的增大，残余强度在降低；竖向应力越大，残余强度越大[8]。Skempton研究表明，残余强度是指以缓慢剪切速率达到相当大的剪切位移条件下所达到的最小剪切强度值，剪切速率对黏土残余强度是有影响的[9]。因此，本文以合肥地区弱膨胀土为研究对象，采用全自动残余强度试验仪，在慢剪排水条件下，进行不同初始含水率、不同竖向应力作用下的残余强度试验。根据双因素数值方差分析，建立数学统计模型，确定初始含水率和竖向应力对膨胀土残余强度是否存在影响，如果有影响，并确定影响顺序。

二、试验方案

试验土样为原状土。土样取自合肥市瑶海区、包河区、蜀山区、庐阳区，共计80个土样。以初始含水率17.8%，20.5%，22.6%，25.6%为研究对象，加载竖向应力分别为100kPa、200kPa、300kPa、400kPa。试验仪器见图1。严格按照《土工试验规范》GB/T50123-1999进行，试验步骤如下：

(1)土样进行真空抽气饱和，真空抽气一个大气压下一个小时，饱和时间不宜低于10小时，本试验土样饱和时间控制在12～14小时。一次饱和两个土样，一个做饱和度试验，饱和度达到95%以上时，方可使另外一个土样进行残余强度试验。

(2)土样规格DXh=61.8mm×20mm，按照要求放入试验仪器。启动开关，正向剪切速率为0.02mm/min，按剪切位移0.02mm自动计数一次，最大剪切位移为8～10mm。

(3)第一次正向剪切完成后，启动反向开关，反推速率应小于0.6mm/min，本次试验为了保证能够准确退回原点，反推速率根据最大剪切位移计算且控制在0.6mm/min以内。

(4)等待30min后进行第二次剪切，如此反复多次，直至最后两次剪切时测力计读数接近。本次试验反复剪切四次，总剪切位移在32～40mm。

(5)剪切结束后，整理试验数据，绘制不同初始含水率下，不同竖向应力作用下剪应力-剪位移关系曲线。土样试验结果见图2。

图1 全自动残余强度试验仪

图2 反复四次剪切的土样

三、试验结果分析

图3～5是初始含水率为17.8%时，分别在竖向应力为200kPa、300kPa、400kPa作用下，经过四次反复剪切的剪应力-剪应变关系曲线。图中可以看出，经过四次剪切，膨胀土的峰值应力在下降，且第二次相对于第一次峰值降低很大，主要是因为经过第一次剪切，膨胀土的强度指标黏聚力急剧下降。随后的三次剪切使得剪切面颗粒不断发生定向排列，直至剪切面趋于光滑，因此从图中可以看出，第三次和第四次剪切峰值很接近，剪切曲线基本重合，处于稳定状态，因此可以第四次剪切峰值作为稳定的膨胀土残余强度。

图3 200 kpa作用下的剪应力-剪位移曲线

图4 300 kpa作用下的剪应力-剪位移曲线

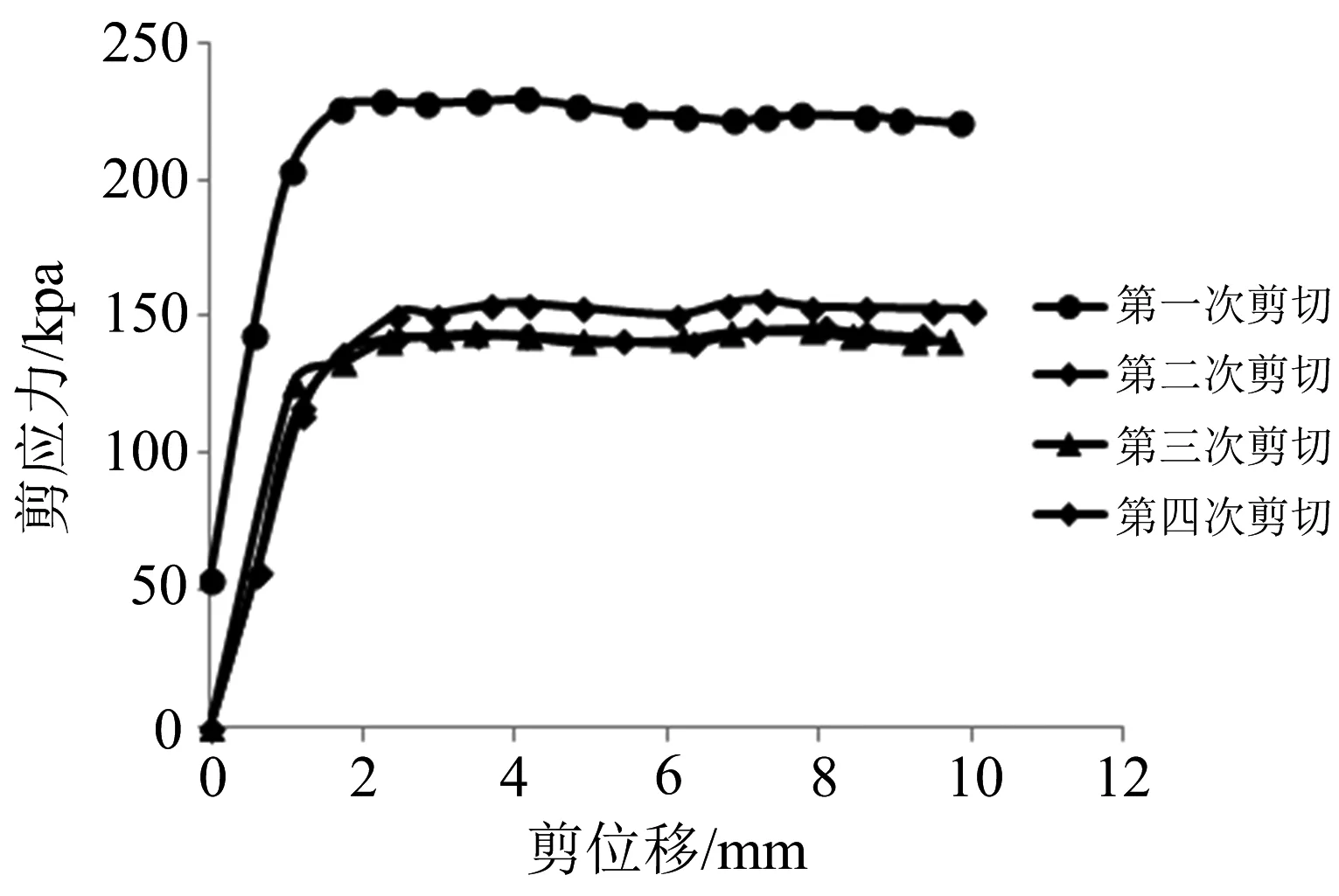
图5 400 kpa作用下的剪应力-剪位移曲线

不同初始含水率，在不同竖向应力作用下的膨胀土残余强度如表1所示。表1显示，在相同竖向应力作用下，随着初始含水率的增加，残余强度在降低。当竖向应力为200 kPa，初始含水率为25.6%时，残余强度下降幅度最大，达到60.1%。这点与膨胀土抗剪强度与含水率关系的结论是相同的[10]。初始含水率相同时，随着竖向应力的增大，残余强度在增加。主要是因为竖向应力的增加，可以增大土颗粒间的摩擦力，从而提高了残余强度。当初始含水率为17.8%，竖向应力为400 kPa时，残余强度最高增加了84.6 kPa，增幅达到137.1%。

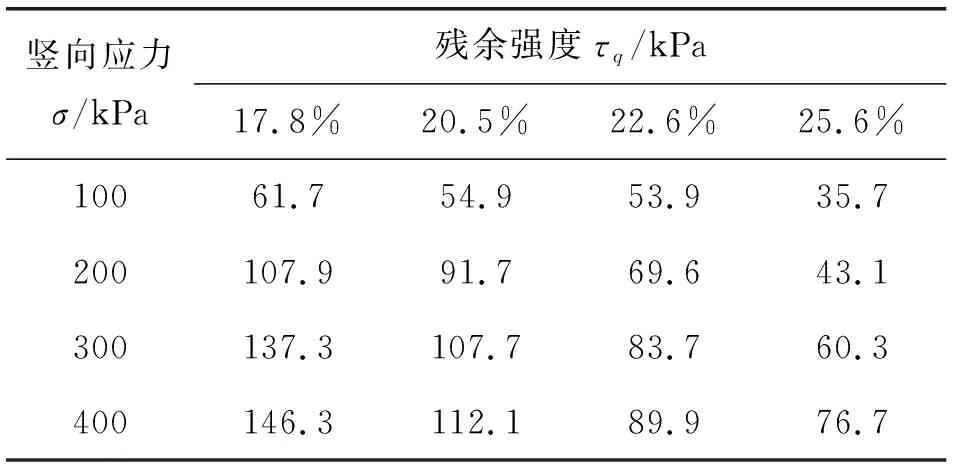
表1 膨胀土残余强度结果

四、双因素方差分析

从数据结果分析，在慢剪排水条件下进行膨胀土残余强度的测定，初始含水率和竖向应力对膨胀土的残余强度是有影响的，为了分析初始含水率与竖向应力对残余强度的影响是否显著，可以通过双因素方差分析进一步明确。双因素方差分析就是利用试验数据来推断两个因素在其水平发生变化时对试验指标是否产生显著影响的一种数理统计方法。通过方差分析，结合数理统计结果，也能够确定两因素的影响顺序。根据试验影响指标，把竖向应力看成因素A，有r=4个水平；初始含水率看成因素B，有s=4个水平。双因素方差分析数据结构表如下：

表2 双因素方差分析数据结构表

假设yij之间相互独立，yij～N(uij，σ2)，则ηij=uij+eij，eij之间独立同分布，eij～N(0，σ2)。则数学统计模型为：

(1)

式(1)中：αi为因素A在水平i下对试验指标的效应；βj为因素B在水平j下对试验指标的效应。

方差分析主要任务是分析因素A和因素B对试验指标的影响大小。本次试验取显著水平α=0.95，提出如下假设：

对因素A，原假设为因素A对试验指标影响不显著，等价于

H01：α1=α2=α3=α4=0

对因素B，原假设为因素B对试验指标影响不显著，等价于

H02：β1=β2=β3=β4=0

利用平方和分解公式中的各种离差平方和，构造F统计量。记：

(2)

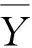
(3)

若FA≥Fα[r-1,(r-1)(s-1)],则拒绝H01，即认为因素A对试验结果有显著影响；若FB≥Fα[r-1,(r-1)(s-1)]，则拒绝H02，即认为因素B对试验结果有显著影响。相关统计量结果如表3所示。

从表3的结果显示，FA=18.6>F0.95(3,9)=8.81，则拒绝H01；FB=20.2>F0.95(3,9)=8.81，则拒绝H02。通过双因素方差分析可证明竖向应力和初始含水率对膨胀土的残余强度有显著影响。由于FB>FA，因此初始含水率对膨胀土残余强度的影响最大，其次是竖向应力的影响。

表3 双因素方差分析

五、结论

(1)经过四次反复剪切，膨胀土剪切面颗粒完成新的定向排列，第三次和第四次的剪切峰值基本接近，说明膨胀土剪切强度处于稳定状态，可以第四次剪切峰值作为膨胀土残余强度。为合肥地区膨胀土残余强度的确定提供了可靠的试验方法。

(2)在相同竖向应力作用下，随着初始含水率的增加，残余强度在降低；初始含水率相同时，随着竖向应力的增大，残余强度在增加。残余强度与初始含水率、竖向应力的变化关系，为合肥地区膨胀土边坡稳定性分析，提供了理论指导。

(3)通过双因素方差分析，证明竖向应力和初始含水率对膨胀土的残余强度有显著影响。其中初始含水率对膨胀土残余强度的影响最大，其次是竖向应力的影响。为合肥地区膨胀土边坡稳定性的影响因素提供了理论依据。