太赫兹金属光子晶体结构研究
2018-09-14杨冰洋许恩豪
陈 麟, 杨冰洋, 雍 有, 杨 涵, 杨 洁, 许恩豪
(1.上海理工大学 上海市现代光学系统重点实验室, 上海 200093;2.上海理工大学 光电信息与计算机工程学院, 上海 200093)
引 言
在20世纪70年代末,Yeh和Yariv首次报道了周期性平面结构的表面波,随后带动了微纳光子学领域相关技术的发展。特别是在Ebbesen等发现在金属膜中的亚波长孔阵列能够实现特定波长的超常透射特性后[1],这个现象引起了广泛关注[2-3]。Pendry等理论证明了表面等离子体的存在[4],2002年,Thio等报道在牛眼结构中也有类似的现象[5],不久之后,Degiron等在实验中对单侧和双侧牛眼结构的传输信号进行了比较分析[6]。由于金属孔阵列的光学厚度是由介电衬底涂覆的,表面等离子体可以在可见光和太赫兹范围内激发,并在透射谱中出现Fano共振[7-25]。当金属孔阵列的周期与电磁波在谐振频率上的波长可比拟时,表面波的作用起主导作用[26-28]。与金属孔阵列相关的内容可以在文献[29-30]中找到。
对比金属膜厚度只有亚微米量级的金属孔阵列,其金属光子晶体因有着能够控制电磁波传播的潜能而受到广泛关注。此时金属层的厚度范围远超过金属孔阵列,达到波长量级,表明金属光子晶体有着独有的光子能带与表面等离子激元性质。由于金属光子晶体在太赫兹频段易于制造,大量研究关注于太赫兹频段内表面波引起的金属光子晶体的传播特性上,例如,金属光子晶体表面电场的强约束使我们有机会研究具有高灵敏度和大面积成像特性的传感技术。根据透射谱的角度变化可建立表面等离子模式引起的光子能带结构。近年来,在太赫兹频段内,正方形阵列的金属光子晶体的超透射现象已有报道。对于三角形阵列,作者所在的课题组对这种表面波的色散特性在太赫兹域通过角分辨光谱进行了详细研究。本文基于之前的成果讨论了金属光子晶体中ΓK和ΓM方向的完整太赫兹光子能带图及其角度依赖特性。
1 利用三维时域有限差分法分析超透射
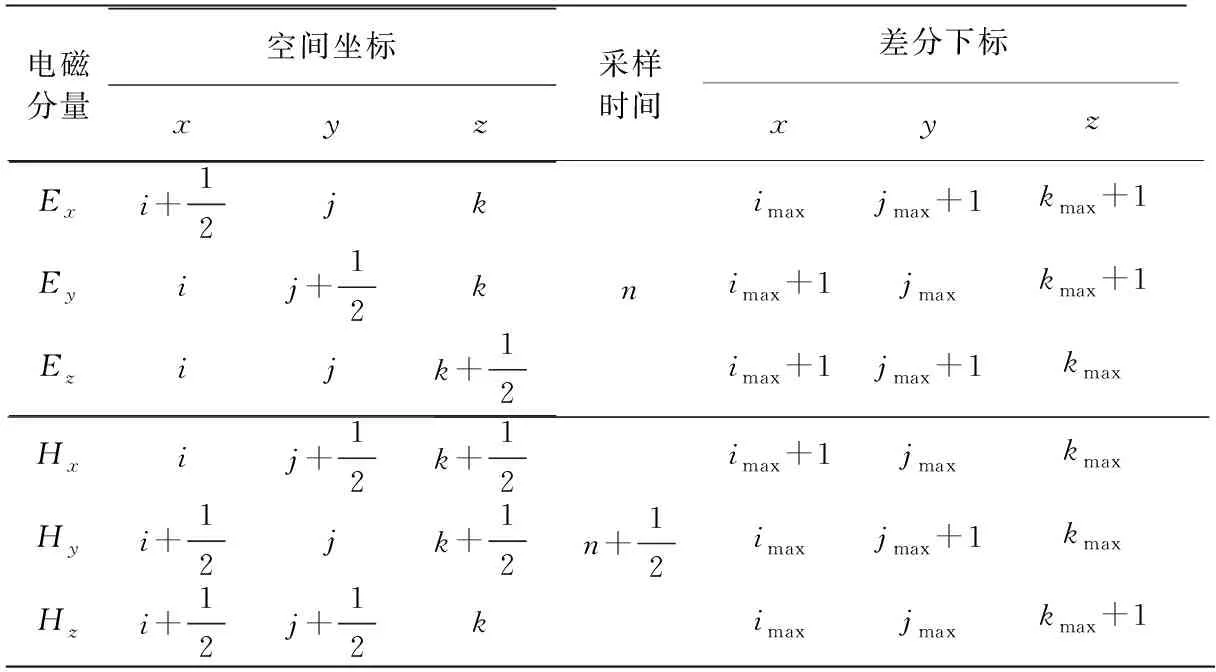
三维时域有限差分法是通过离散化的方式精确求解麦克斯韦方程。通过使用Yee元胞,如图1所示,每个部分的精确坐标如表1所示,并可表示为
F(x,y,z;t)=F(iΔx,jΔy,kΔz;nΔt)=Fn(i,j,k)
(1)
式中:i、j和k为不同坐标轴上的Yee单元序列;n为计算的时间步骤;x、y、z和t分别为空间坐标和时间坐标。

图1 Yee单元上的电磁场分量Fig.1 Electromagnetic field components on Yee unit
电磁分量空间坐标xyz采样时间差分下标xyzExi+12jkEyij+12kEzijk+12nimaxjmax+1kmax+1imax+1jmaxkmax+1imax+1jmax+1kmaxHxij+12k+12Hyi+12jk+12Hzi+12j+12kn+12imax+1jmaxkmaximaxjmax+1kmaximaxjmaxkmax+1
利用表2所示的对偶关系可导出离散的麦克斯韦方程满足的一系列的递归方程组,其物理意义是表示了不同传播位置处的电场分布。
在图2所示的吸收边界中,选择基于吸收边界条件算法的完全匹配层。

表2 递归方程的对偶关系Tab.2 The dual relation of the recursion equation

图2 区域的划分和样品,输入和输出面的位置Fig.2 The division of domain and the location of sample,input and output plane
我们利用三角排列的金属光子晶体来验证上述三维时域有限差分算法的准确性。如图3所示,所给出的金属光子晶体由在铝(Al)板上的三角形孔阵列组成,参数为t=0.25 mm,d=0.7 mm,p=1.13 mm,太赫兹波垂直入射到金属光子晶体平面上。金属光子晶体几何尺寸为50 mm,用以提供足够的周期性延伸。
在太赫兹范围内,铝的介电常数可以用Drude模型来描述,即
(2)
式中:ω为入射波的角频率;ε(ω)=1;ωp=2.276×1016rad/s;γ=7.141×1016rad/s。
此时,透射率T可以表示为
(3)
式中Win为入射波的总能量。图4显示了Ex和Hz在垂直x轴的结构对称平面上的场分布。图4(a)和(b)的场分布表明,电磁波的方向被结构束缚,在金属和空气的界面上确实存在表面等离子波[29]。
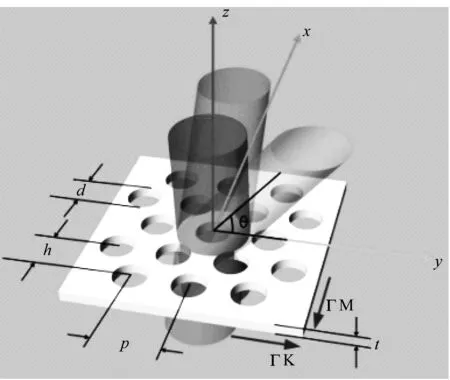
图3 尺寸为t=0.25 mm,d=0.7 mm和p=1.13 mm的金属光子晶体的示意图,以及沿着x(ΓM)或y(ΓK)方向斜入射的示意图Fig.3 Schematics of a metallic PC with the regarding dimension,t=0.25 mm,d=0.7 mm,and p=1.13 mm,a nd θ the polar angle of the incident radiation along x(ΓM) or y(ΓK) directions

图4 Ex和Hz的场分布Fig.4 Field distributions of Ex and Hz
如图5所示为入射波的透射率与入射波频率的关系。很容易看出,在共振频率0.26 THz时,透光率高达76.52%。
为了验证上述理论结果,我们利用太赫兹时域光谱仪测量了上述样品的透射谱[30-32]。参考光谱和输出信号光谱如图6所示,输出谱的谐振频率为0.27 THz。计算结果与实验结果吻合较好。

图5 基于三维时域有限差分方法的透射率曲线Fig.5 Transmittance based on 3D-FDTD method
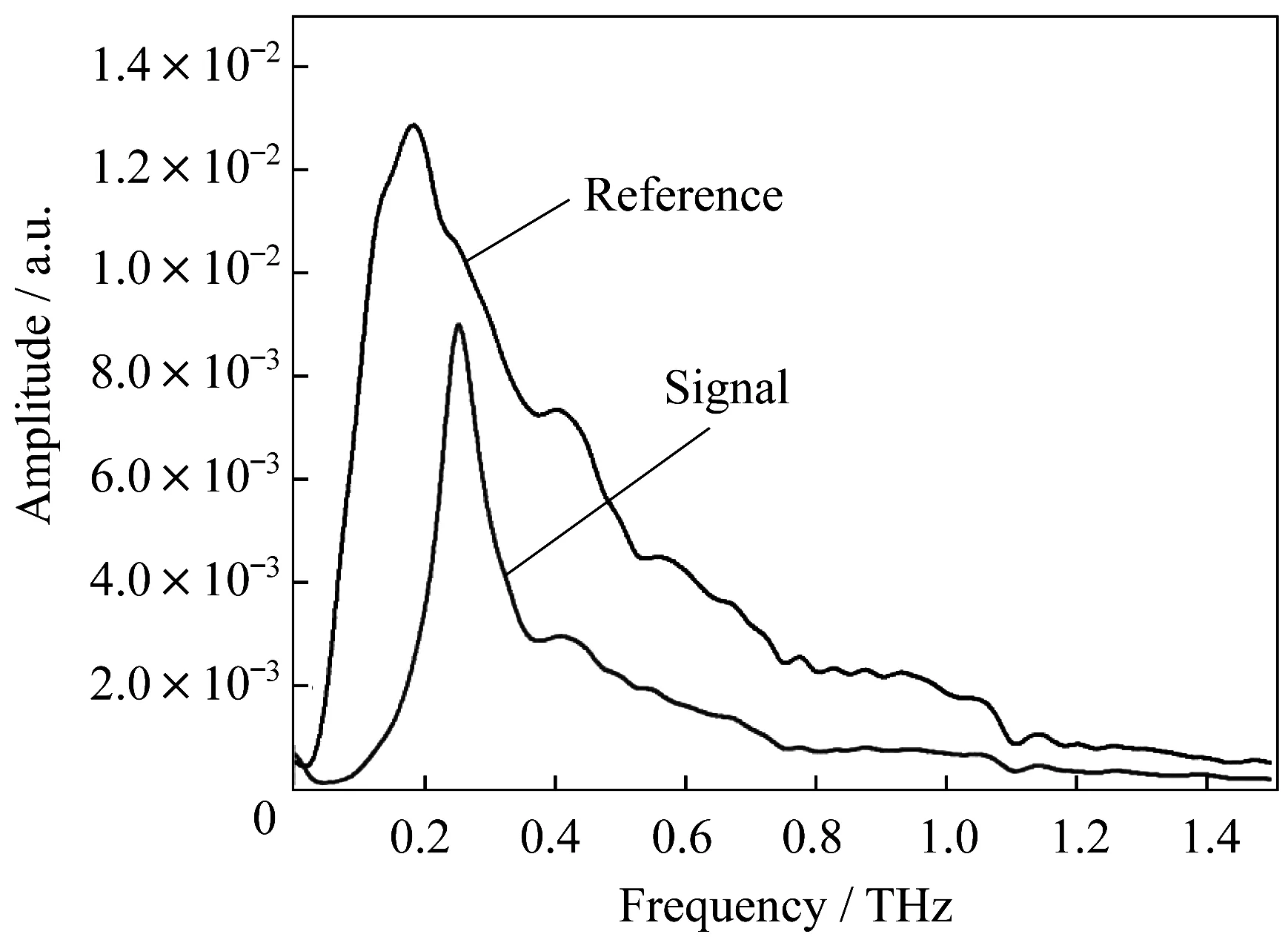
图6 使用太赫兹时域光谱仪的实验结果Fig.6 Experimental results by using THz-TDS
2 金属光子晶体上的ΓM和ΓK方向上太赫兹光子能带图
我们重点研究三角阵列的金属光子晶体的完整光子能带图。结构示意图如图3所示,其中ΓM和ΓK方向已在图中标出。考虑到金属光子晶体中的波矢和入射波波矢之间相互作用及匹配条件,如果入射太赫兹波在金属光子晶体上与光栅常数p、入射角θ等参数密切相关,则金属光子晶体平面上的表面波矢量ksur可表示如下[24]:
|ksur|=|kx+mGx+nGy|
(4)
式中:m和n为整数;kx为x方向传播的的波矢分量;Gx和Gy为六边形网格中沿x和y方向的倒格矢。kx又可定义为
(5)
式中k∥为平行于金属光子晶体表面的波矢。Gx、Gy可以表示为:
(6)
(7)
则式(4)可以改写为
(8)
当电磁波从外部入射时,金属光子晶体可以支持表面波,这种表面波在金属和空气的界面处传播,并耦合到自由空间中[28]。在孔直径缩小至零时,即在占空比为零的晶格近似中,表面波波矢可以表示为
(9)
式中:ksp为表面等离子体共振矢量;fsp为表面波的谐振频率;ε1为覆盖金属光子晶体的材料介电常数,ε2为金属的介电常数。Al的介电常数在1 THz波段为-44 900+i511 000[33-34],这比可见光范围大得多[35]。所以式(9)右边根号内的项可近似为1。
根据式(8)和式(9),我们画出了金属光子晶体在ΓK和ΓM方向的完整的光子能带图,如图7所示。为了方便起见,图7中的色散图折叠到第一布里渊区里[36]。在ΓM方向,有一个强的谐振峰色散线和三个弱的色散线,强色散线对应的是主表面波的(-1,0)模式,我们发现(-1,0)模式有陡峭的负斜率,与真空中的光色散线几乎相同。在ΓK方向,有一个强的谐振峰线和两个弱谐振峰线,强谐振峰线对应于表面波(0,-1)模式。
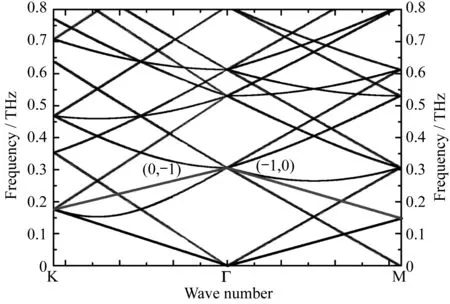
图7 金属光子晶体在ΓM和ΓK的光子能带图Fig.7 Photonic band of metallic PC for ΓM and ΓK directions
3 入射角对透射的影响以及模式分裂效应
本节讨论表面等离子体激元的共振峰随入射角的变化情况。太赫兹波在ΓM和ΓK两个方向上以一定的入射角入射,如图3所示。从公式(8)和(9)可以知道,表面波的共振频率fsp不仅受孔阵的几何构造影响,还受入射角θ的影响。显而易见,k∥可以表示为
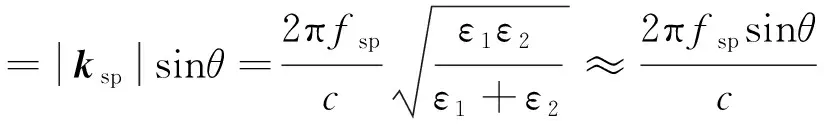
(10)
如果我们定义f0是在垂直入射时的零介等离子体共振频率,并定义归一化共振频率为
(11)
利用式(8)、式(10)和式(11),我们可以得到表面等离子体的共振频率为
(12)
为了验证仿真结果,我们在实验中将金属光子晶体样品沿x轴方向和y轴方向旋转,以代替不同的太赫兹波入射角。如图8所示,当入射角不是垂直入射时,透射峰会分裂成两个峰,而峰值共振频率会发生红移。图9显示了由式(12)得到的金属光子晶体在表面波模式下的色散特性以及不同入射角产生的模式分裂效应。当入射波垂直照射在表面时,太赫兹波的能量与金属光子晶体的本征模耦合。随着入射波的改变,本征模会分为若干个模式,每个模式都有自身的色散曲线(如图9)。本征模的分裂与布里渊区有关,由金属光子晶体的几何结构决定的。从图8和图9可以看出,当入射角改变时,金属光子晶体表面波模式的色散和与共振频率对应的真空中的光色散线之间的相互作用点发生了移动(如图9(a)中的点A,B,C,D和图9(b)中的点E,F,G,H)和分离(如图9(a)中的点A和I)。当极角为0°~40°(ΓM方向)且模式为(-1,0)、(0,1)和(-1,1)时,金属光子晶体的共振频率如图10所示,从图10可以看到,实验结果与理论计算得到的结果相吻合。

图8 太赫兹波在金属光子晶体上透射的特性Fig.8 The THz transmission property from metallic PC
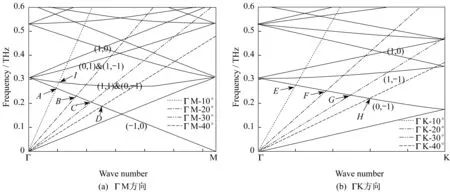
图9 金属表面等离子波模式的色散,光在真空中不同的角度Fig.9 Dispersions of plasma wave pattern on metal surface and the light in vacuum at different angle
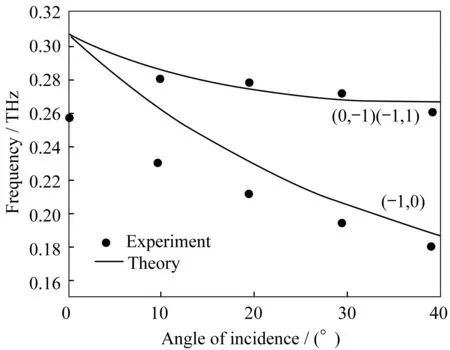
图10 理论与实验结果的共振频率Fig.10 Theoretical and experimental results of resonance frequency
4 结 论
简要讨论了金属光子晶体的异常传输,光子能带图和非对称入射下的模式分裂效应。该研究将对从事相关现象研究的人员有着借鉴作用。因此,本文给出的结果不仅太赫兹波段,同样在滤波、成像和其他学科具有潜在的应用。未来,金属光子晶体结构在太赫兹近场显微术、高分辨率太赫兹成像和可调谐太赫兹滤光片中的应用仍有许多未知的重要现象有待研究和发现。
