基于后向光散射的颗粒测量技术研究
2018-09-14卢松芳沈建琪
卢松芳, 沈建琪
(上海理工大学 理学院, 上海 200093)
引 言
随着工业化和城市化的快速发展,全球大气污染日益严重,大气颗粒物已成为城市(尤其是东亚城市)的首要空气污染物[1-3]。颗粒物对环境和人体健康危害非常大,有必要对颗粒物污染情况进行准确监测和深入研究。目前常用的颗粒测量方法主要有基于消光原理的光浊度法和基于光散射的颗粒计数法[4]。光浊度法只有配合颗粒粒径分布的测量才能得到准确的颗粒浓度信息,而光散射颗粒计数法是利用散射光能量与颗粒粒径的对应关系得到颗粒的粒径信息,且对低浓度颗粒系的测量能力有明显提高。光散射法以其测量范围宽、测量速度快、适用性广等优点被广泛应用。本文基于后向散射光自混频干涉技术[5-9]研究大气颗粒物在线实时监测技术,通过理论分析、数值计算和实验验证,研究后向散射光能与颗粒粒径、颗粒折射率及颗粒浓度之间的变化特性。
1 原理及模拟计算
1.1 后向散射光能计算原理
大气颗粒物测试原理如图1所示,激光器发出的激光经透镜组会聚到样品池内的流动颗粒上,颗粒的后向散射光经相同透镜组反馈回激光内腔,与原始激光发生自混频,小部分自混频信号从激光器后端面射出,被置于后方的探测器接收。
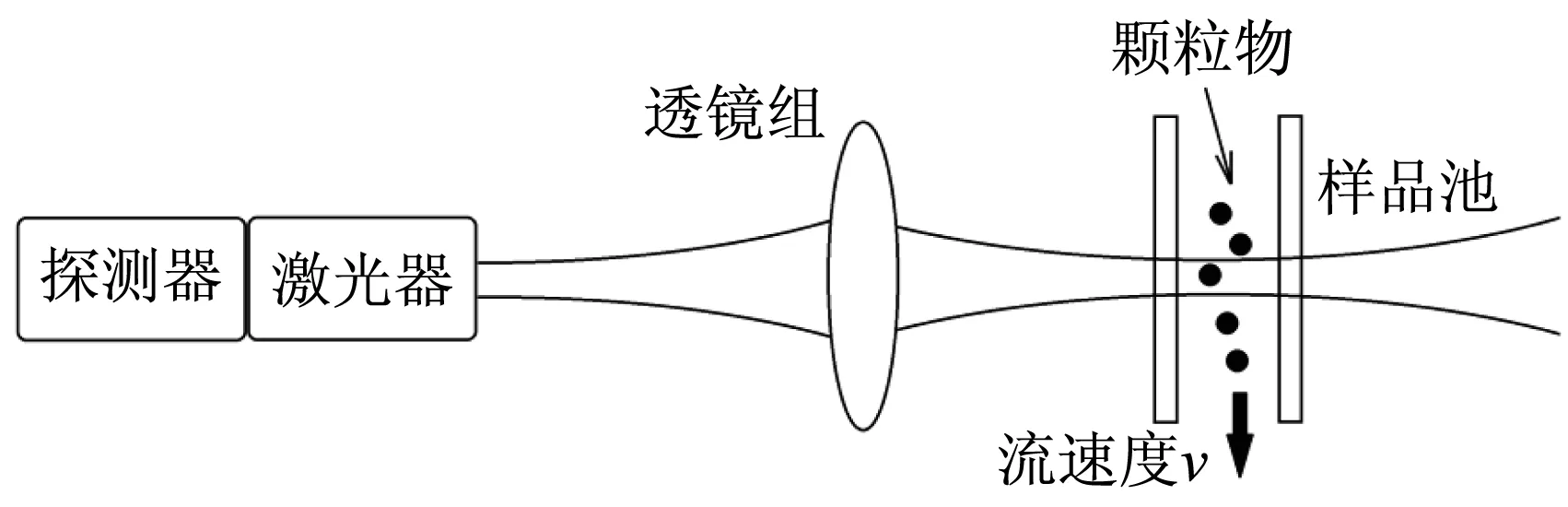
图1 大气颗粒物测试原理图Fig.1 Schematic diagram of optical system for measuring the airborne particulates
图2是基于广义Mie理论[10-11]对颗粒物散射光空间分布的计算模型。设一单色高斯光束入射波束沿z轴正向传播,束腰中心为O,束腰半径为ω,偏离z轴的颗粒中心OP在光束坐标系O-xyz中的坐标为(x0,y0,z0),Op-xpypzp是颗粒坐标系。在研究球形颗粒的散射问题时,通常会引入无因次粒径参量α=2πa/λ,其中λ是入射光在真空中的波长,a是球形颗粒的半径。
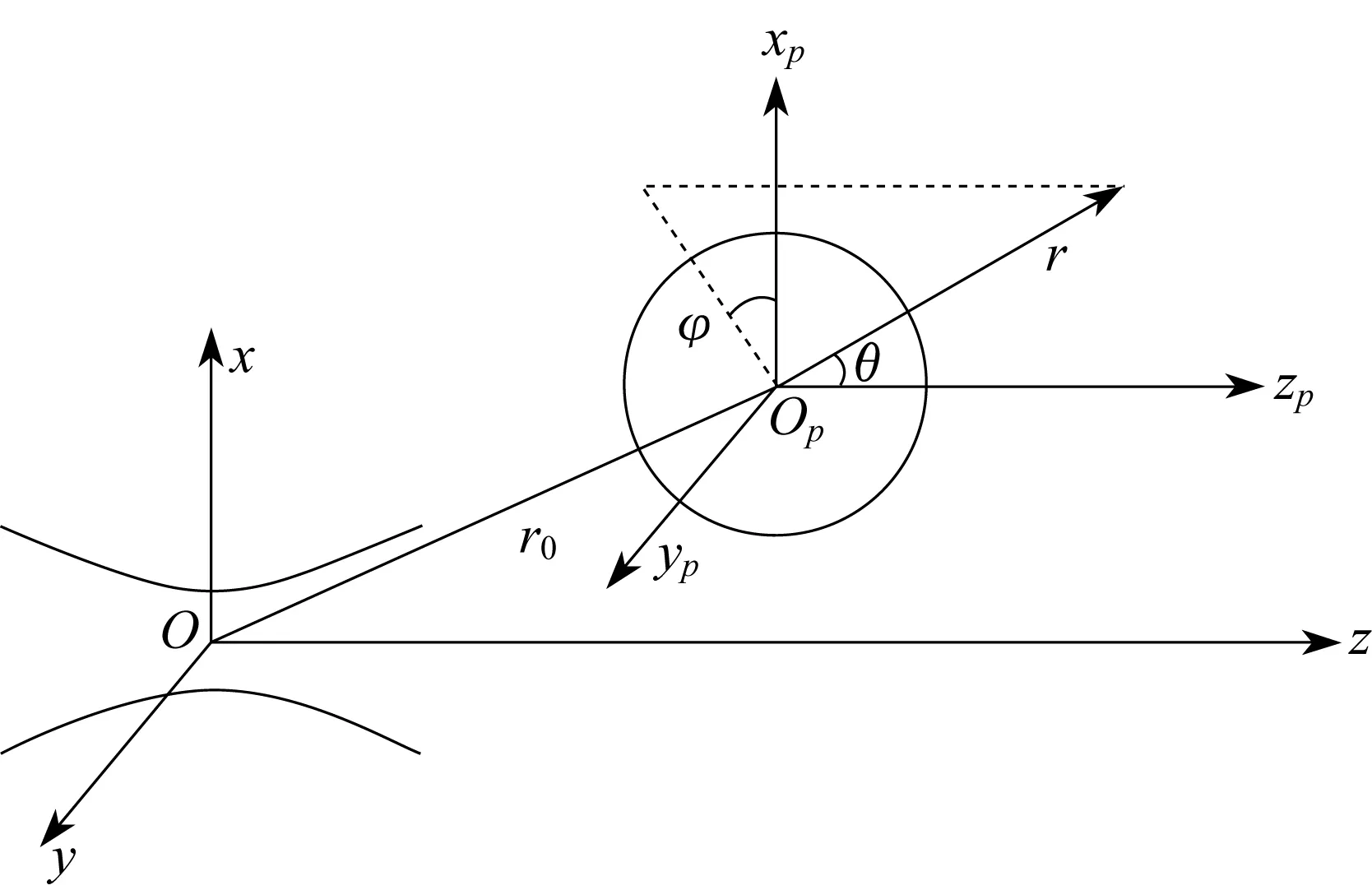
图2 球形粒子对高斯光束的散射Fig.2 Light scattering of a Gaussian beam by a spherical particle
根据图1所示的后向散射光探测装置,颗粒散射光能量可表示为
(1)
式中:Isca为散射光强且Isca=|S1(θ,φ)|2+|S2(θ,φ)|2,S1(θ,φ)和S2(θ,φ)为散射振幅函数;rmax为后向散射光接收透镜系统的有效半径。
1.2 颗粒粒径对散射光能分布的影响
颗粒的光散射特性与颗粒粒径密切相关[1],颗粒粒径不同,散射光能分布明显不同。基于颗粒的后向散射原理编写程序计算颗粒后向散射光能,改变参数获得颗粒散射光能与颗粒粒径及颗粒折射率之间的对应关系。设置高斯光束的束腰半径ω=5.0 μm,改变颗粒粒径大小,由模拟计算可知:在小颗粒情况下,后向散射光能随着颗粒粒径变化在对数坐标上呈线性变化关系,如图3(a)所示;对于非吸收性颗粒或弱吸收性的大颗粒,散射光能随颗粒粒径变化呈周期变化特性,其周期约为Δa=0.276 8 μm,该周期转化为颗粒粒径无因次参数后与颗粒折射率m的乘积是一个常数,即Δαm=π,对于吸收性颗粒,当折射率虚部大于一定数值时,散射光能随颗粒粒径变化不再呈现振荡现象,如图3(b)中m=1.33+i0.01和m=1.33+i0.1。
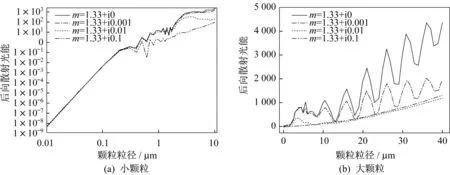
图3 颗粒的后向散射光能分布随颗粒粒径的变化Fig.3 Dependence of the backward scattered light energy on the particle size
在束腰半径ω=5 μm情况下,计算折射率为m=1.33+i0.001、颗粒半径分别为a=8 μm和a=16 μm的弱吸收性颗粒的后向散射光能随颗粒在光束中位置变化的规律。图4给出了计算结果,其中横坐标表示颗粒在垂直于光束传播方向且包含光束束腰中心的平面内与束腰中心之间的距离。可以看出:对于a=8 μm的颗粒,其散射光能呈双峰分布且二个峰值对称分布,颗粒后向散射光能的最大值偏离束腰区一定距离,并不在束腰中心处;对于a=16 μm的颗粒,模拟计算得到的波形呈三峰分布,散射光能在束腰中心位置出现一个很强的峰,在偏离束腰位置有两个对称波峰且峰值较小。经过大量模拟计算发现,颗粒后向散射光能的波形在a≥1.6ω时呈双峰或者三峰分布。散射光能与颗粒粒径呈非线性关系且具有一定的周期变化规律。

图4 后向散射光能随颗粒在光束中位置变化规律,颗粒折射率为m=1.33+i0.001Fig.4 Profile of backward scattering energy via the location of particle in the beam where the refractive index m=1.33+i0.001
针对折射率为m=1.33+i0.01的颗粒,散射光能分布的计算结果如图5所示。可以看出:在颗粒半径与束腰半径之间满足a=1.6ω时,颗粒的后向散射光能的波形呈对称双峰分布;当颗粒a>1.6ω时,颗粒散射光能的波形为单峰分布。进一步增大颗粒折射率虚部,计算结果基本类似。即颗粒后向散射光能在颗粒折射率虚部较大且满足一定条件(a>1.6ω)时,颗粒的散射光能呈单峰分布且散射光能峰值不再随颗粒粒径振荡变化。

图5 后向散射光能随颗粒在光束中位置变化规律,颗粒折射率为m=1.33+i0.01Fig.5 Profile of backward scattering energy via the location of particle in the beam where the refractive index m=1.33+i0.01
1.3 颗粒折射率对散射光能分布的影响
颗粒的光散射特性与粒径大小及其折射率密切相关。取固定粒径的颗粒,改变颗粒折射率虚部的值进行数值计算。对数据分析处理得到图6所示结果:对于非吸收性颗粒,在折射率实部相对较大时,小颗粒的后向散射光能分布随折射率变化呈周期振荡规律;颗粒半径a分别为2.0 μm、3.0 μm、4.0 μm、5.0 μm时,与其相对应的折射率周期Δm分别为0.158 2、0.105 5、0.079 1、0.063 3。可以得到折射率周期与颗粒半径参量的乘积是一个常数,即αΔm=π。随着颗粒半径增大,周期振荡规律越明显,而且在较小的折射率下散射光能就会有周期振荡的规律出现。
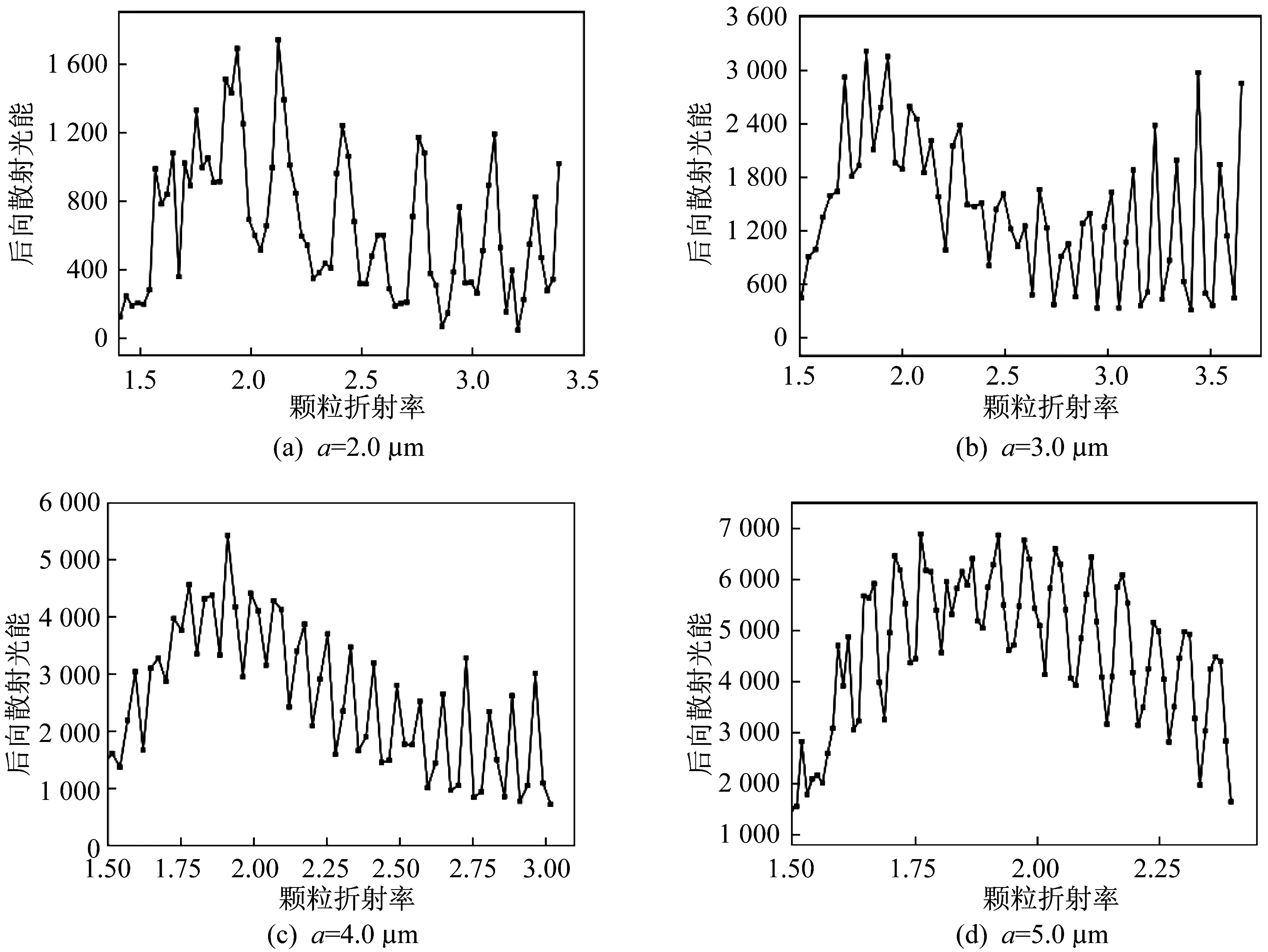
图6 吸收性颗粒的后向散射光能与颗粒折射率关系Fig.6 Variation of backward scattering energy due to the increasing refractive index of the particles
由图6可知,颗粒散射光能随颗粒折射率变化呈周期变化特性。对于非吸收性颗粒,无法避免折射率带来的影响,但在实际测量中,大气颗粒物大都是吸收性颗粒。图7给出了不同吸收系数颗粒的后向散射光能分布与颗粒粒径的对应关系。随着吸收系数增大,后向散射光能逐渐减弱,这是由于颗粒对入射光的吸收导致了其散射能力的降低。
1.4 颗粒位置对散射光能分布的影响
颗粒的后向散射光能还与颗粒通过束腰区的位置有关,同一时间经过测量区不同位置得到的反馈信号高度有所不同。保持颗粒半径2.0 μm、折射率m=1.33+i0.01不变,通过设置颗粒偏离束腰中心的参数,得到吸收性颗粒后向散射光能与颗粒偏离束腰中心距离的关系,如图8所示。由图8可知颗粒偏离束腰区越远,其后向散射光能越小,这与高斯光束的特殊能量分布方式相吻合。
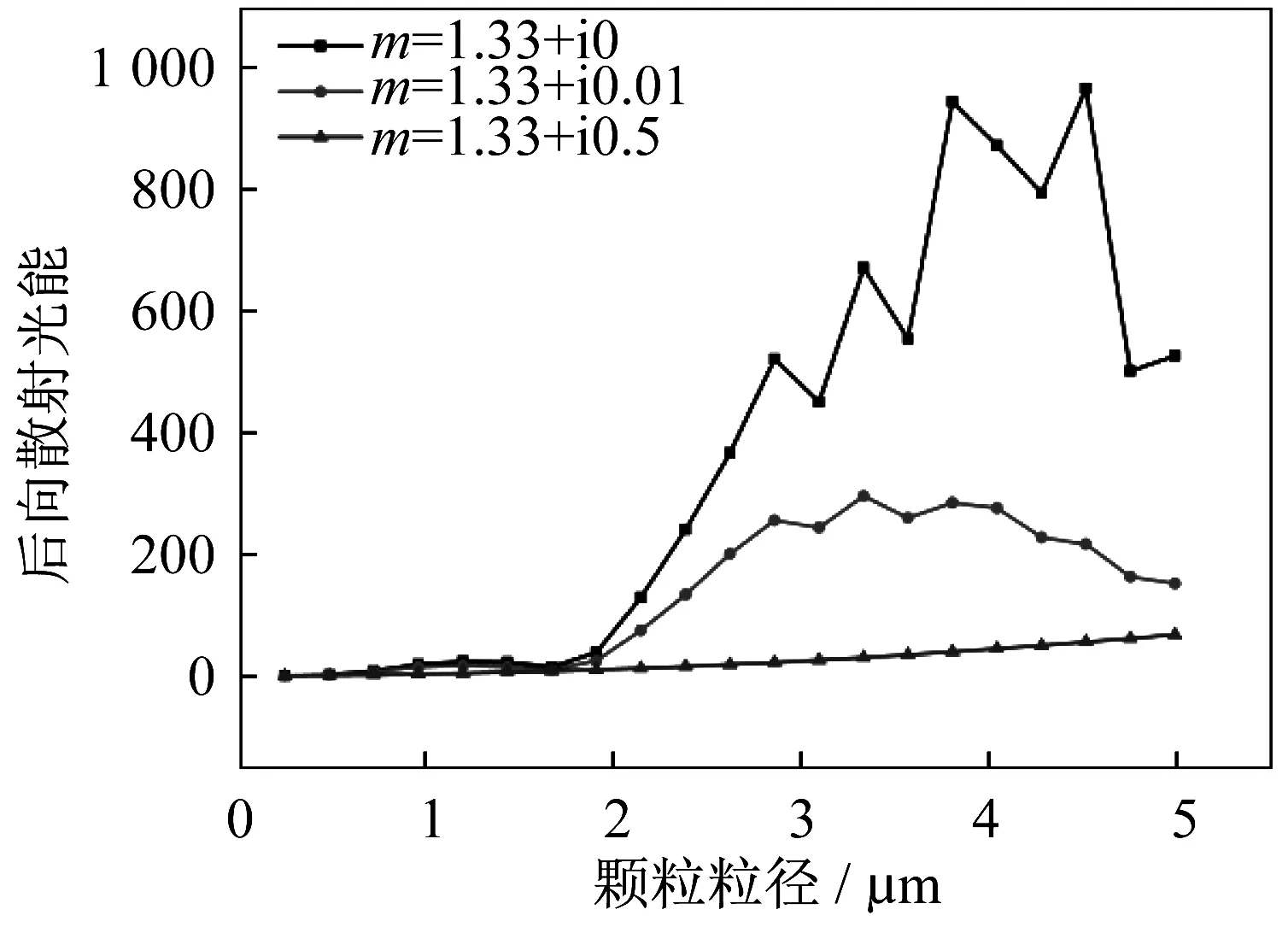
图7 不同折射率下的后向散射光能分布与颗粒半径的对应关系Fig.7 Dependence of backward scattering energy on the particle size for different refractive indices

图8 颗粒后向散射光能随颗粒通过束腰区位置的分布Fig.8 Distribution of backward scattering energy with different waist area
2 实验验证
2.1 后向散射信号与小颗粒半径的关系
根据图1的实验原理搭建实验平台,激光器是从THORLABS公司购买的型号为HL6738MG的半导体激光器,光束束腰半径为ω=9 μm。所采用的颗粒试样是从海岸鸿蒙采购的聚苯乙烯标准颗粒。在丹东百特生产的BT-800自动循环进样系统(分散介质为水)中分别滴入颗粒半径为0.5 μm、0.9 μm、1.5 μm和2.1 μm的聚苯乙烯标准颗粒,依次进行实验。循环进样系统采用2 500档位的最大循环速度,以期在软件采集周期内采集到更多的响应信号。用四川拓普公司的topview2000示波器模拟系统进行信号采集,采样频率设置为125 kHz,触发方式为内触发,触发电平为0~10 V,设置连续采集保存数据。采集软件得到的颗粒响应信号中含有较多的单峰波形,根据已有的实验数据,考虑到通过束腰区位置不同带来的误差,选取合适的实验数据进行Origin高斯拟合,拟合结果如图9所示。
在循环速度一定的情况下,不同粒径的颗粒在通过束腰处的单峰波形的波形幅值及波形宽度均不同。颗粒粒径越大,其单峰波形的幅值及宽度均越大。在相同的循环速度与采样频率下,颗粒粒径较大时,其通过测量区时经历的时间较长,因此宽度较宽。由Origin拟合结果可知,单峰波形得到的实际波形与高斯拟合波形匹配程度很好。需要指出,由于仪器噪声以及来自于环境的轻微震荡等原因,颗粒散射光信号较小的地方存在振荡现象。
2.2 后向散射信号与较大颗粒浓度的关系
设置高斯光束束腰半径ω=9 μm并保持不变。在BT-800自动循环进样系统中依次滴入2滴、4滴、6滴颗粒半径为15.1 μm的标准颗粒,保持循环速度和采样频率不变,连续采集200次并自动保存数据。分析实验数据得到实际观察到的颗粒后向散射响应信号。图10给出了浓度分别为2滴、4滴、6滴标准颗粒的实验采集图,颗粒后向散射响应信号个数随浓度的增大而增多,浓度高时相同时间段内通过测量区的颗粒数愈多,因此软件在相同周期内探测到的信号个数愈多。
对采集到的实验数据进行局部放大,发现实际观察到的响应信号多半呈双峰或者三峰分布,理论分析表明,对于非吸收性颗粒,当颗粒半径与束腰半径之间满足a>1.6ω,颗粒的后向散射光能响应波形呈多峰分布(即双峰或者三峰)。采用Origin软件对多峰分布数据进行高斯曲线拟合,如图11所示,可以看出与实验曲线的拟合度较好。
分析图11(a)所拟合的曲线可得,两个波形的底宽相同,说明这两个波形是由两个同一粒径的颗粒先后经过测量区时的响应信号形成。在图11(b)中,三个峰值来自于三个颗粒先后经过测量区的散射信号,由于颗粒通过测量区时偏离束腰中心的距离不同,导致其后向散射信号的峰值呈现出不同的高度。颗粒散射光信号出现重叠的概率与颗粒浓度有关,当颗粒浓度增大时,信号交叠的概率随之增大。这有可能导致信号计数出现误差。
此外,还探测了颗粒半径为23 μm的吸收性颗粒的后向散射响应信号,实验发现实际得到的波形较多的是单峰波形,选取波形较好的数据并进行局部放大,如图12所示。由图可以看出,随着颗粒半径增大,波形高度与波形宽度均有一定程度的增大。
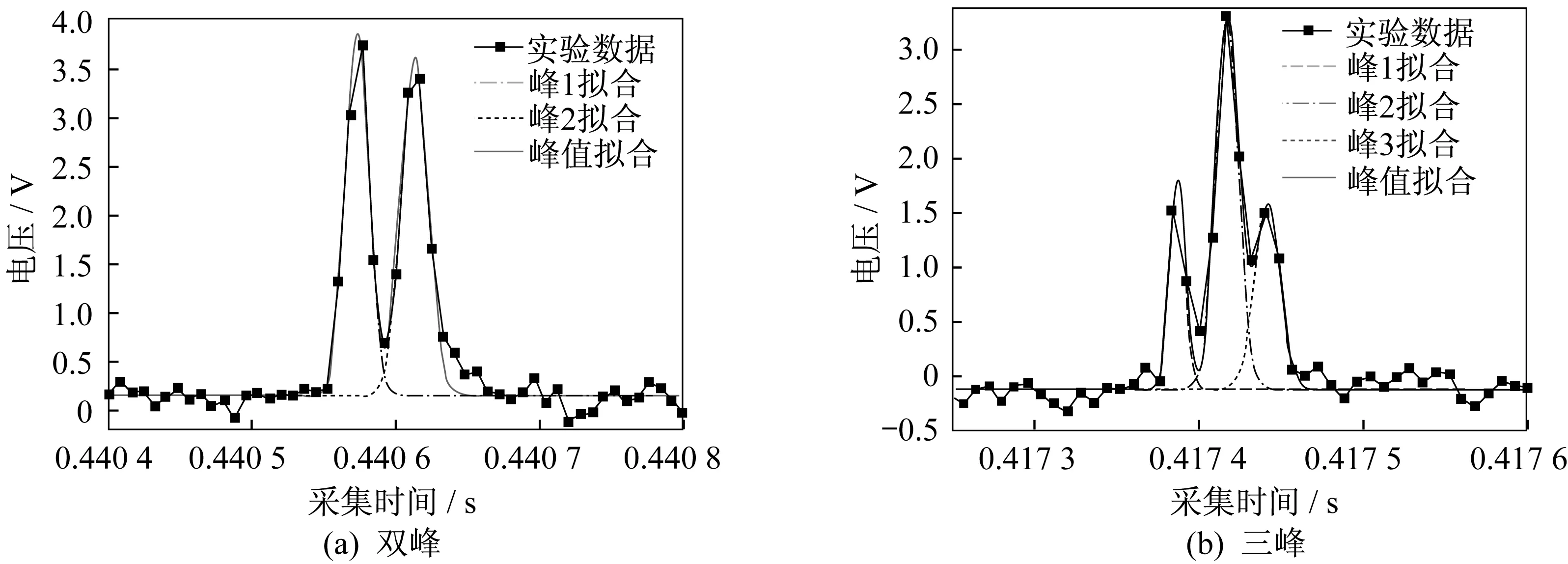
图11 仪器对颗粒的响应多峰的高斯曲线拟合Fig.11 Gaussian curve fitting of more than two peaks
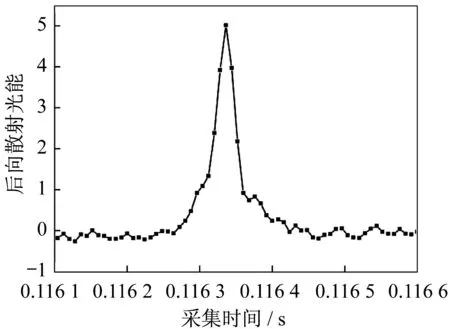
图12 半径为23 μm的颗粒的后向散射信号实验波形Fig.12 Backscatter signal waveform of 23 μm particles in the experiment
从以上分析可知,颗粒的后向散射光能与颗粒粒径、颗粒浓度密切相关,实验验证了颗粒后向散射光能分布随颗粒粒径的变化关系,颗粒浓度对实验研究有很大的影响。
3 结 论
通过理论分析、数值计算及实验验证得到了后向散射光能分布与颗粒粒径、颗粒折射率及颗粒浓度之间的变化规律。理论计算表明,非吸收性和弱吸收颗粒后向散射光能量与颗粒粒径、颗粒折射率呈周期变化规律。实验验证颗粒后向散射光能分布与颗粒粒径的变化关系,与理论模拟吻合。颗粒在测量中的信号个数及信号波形与颗粒浓度有关。
此外,实验发现,由于仪器噪声比较大以及来自于环境的轻微震荡等原因,粒径很小颗粒的散射光信号有可能淹没在噪声中,这个问题还有待进一步解决。
