偏心拉伸铆孔双耳裂纹的应力强度因子计算分析

姚冠兵，万兵，方向，周志祥，吴修波

（1.重庆交通大学，土木工程学院，重庆400074；2.青海省公路科研勘测设计院，青海西宁810001）

在机械、桥梁及水工工程中，相同材料及不同材料间需要相互连接共同受力，不可避免的要对整体结构进行开孔、挖槽等，另外由于材料的不均匀性、以及制作过程中的误差等原因造成结构本身、连接构件及附属构件带裂纹工作往往是不可避免的.特别是在钢结构、钢混组合结构、复合材料结构中铆钉连接是最常见的一种连接方式，带槽孔钢板的断裂损伤问题原理及控制裂纹扩展方法成为亟待解决的问题[1-2].复杂结构在力的作用下破坏以及断裂形式，总是可以看做若干简单破坏或断裂形式的组合，断裂破坏存在3种基本的断裂模式.这3种模式即为张开型—I型断裂、滑移型—II型断裂、撕裂型—III型断裂[3].应力强度因子是断裂力学在研究应力作用下考虑应力和裂纹尺寸这两个因素对裂纹扩展影响而引入的新参数，反映了裂纹尖端附近应力场的强弱.如何简化计算得到适合于工程结构计算的应力强度因子解析式，各国学者做了大量的工作[4-6].弹塑性力学的发展进程与复变函数的发展密不可分，工程结构以材料和边界条件为基础结合实际的工程经验做出判断，解析函数意味着连续结构或者区域内部的值可以通过边界上的边界条件表示，而得到解析函数又是复变函数论的主要目的，这就为复变函数论在工程力学中的应用奠定了基础.其中俄国数学力学家首先应用复变函数论方法解决了平面线弹性静力学问题[7].本文在前人研究的基础上，采用复应力函数及叠加原理计算得到无限宽板上偏心拉伸铆钉双耳裂纹的应力强度因子表达式.

1 方法的提出

1.1 线弹性力学在求解应力强度因子中的应用

线弹性理论是弹塑性力学、断裂力学、固体力学中最基础的力学理论之一，研究对象为理想单元或结构，服从广义胡克定律.本节从线弹性力学的基本理论入手，对无限板上的微孔结构进行分析.

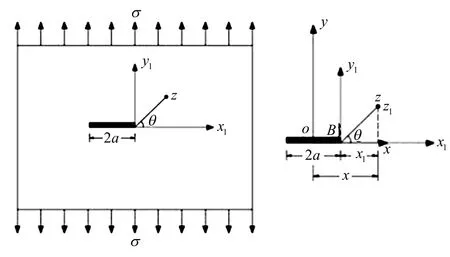
图1 平面应力状态下带中心穿透裂纹

如图1所示的无限平板，为I型断裂；长度L=2a的穿透性裂纹，当无限平板受到均匀的拉应力σ时，其裂纹端部区域的应力分量可以应用弹性理论解得到[8-9]，为便于求解，建立以尖端B点为坐标原点的复数坐标系（如图1），得到复变量z1为：

应力函数表达式：

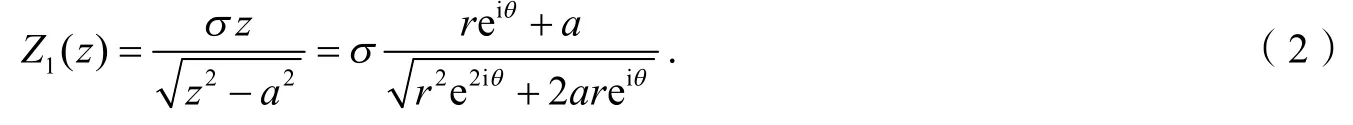
由于裂纹的扩展只取决于裂纹端部区域的应力应变场，对于端部区域有r＜＜a，因此：

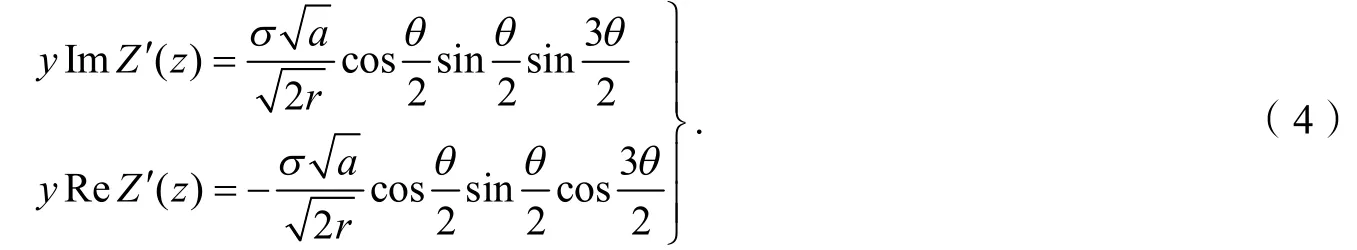
将式（4）代入Ⅰ型经典裂纹问题的Westergaard应力函数得到I型应力函数表达式如式（5），同理得到Ⅱ型断裂的应力表达式如式（6）：

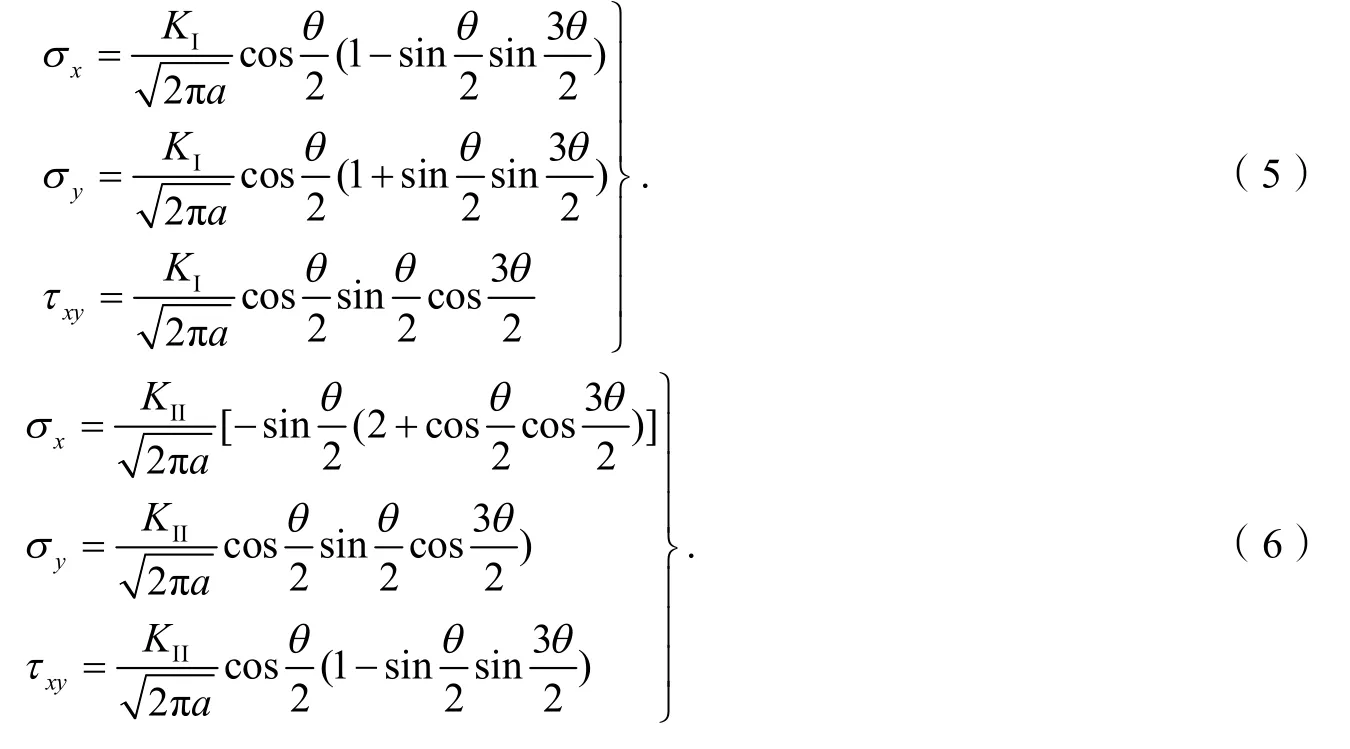
1.2 偏心拉伸铆钉的静力学解

为了得到偏心拉伸铆钉双耳裂纹的应力强度因子，我们从铆钉的线弹性力学弹性阶段静力学受力分析入手，应用叠加原理对铆钉结构进行受力分解.将铆杆对铆孔边缘的偏心集中力分解为垂直于双耳裂纹方向上的张开型力P，平行于裂纹方向上的滑移型力Q，以及铆钉钢板产生的反作用正应力σ、切应力τ.铆钉受力图如图2所示.

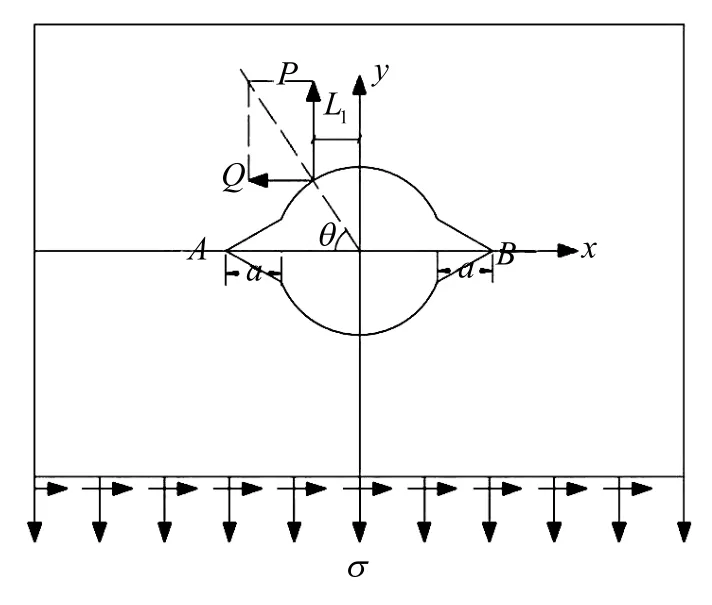
图2 带双耳裂纹偏心拉伸铆钉受力图示

在平面应力状态下，双耳裂纹的破坏形态既可能沿坐标轴y方向张开破坏，也可能沿坐标轴x方向剪切破坏，特别的集中力P作用在近A端裂纹，因此双耳裂纹A端与B端应力强度因子存在差异，需要另行计算.如前所述双耳裂纹偏心拉伸铆钉裂纹扩展破坏属于张开型—Ⅰ型断裂、滑移型—Ⅱ型断裂的复合破坏，为了方便计算我们利用叠加原理对图2受力进行分解，如图3所示.

图3 铆孔偏心受力分解示意图

叠加原理得到aK表达式：

对于图3-b进一步分析可知，裂纹尖端受到了均布应力σ、偏心集中力P的共同作用，可利用叠加原理继续对图3-b受力图示进行分解，如图4所示.分析易知图4-b与图4-f所示铆钉为对称受力，受力特性及变形特性一致，故可以进行合并.

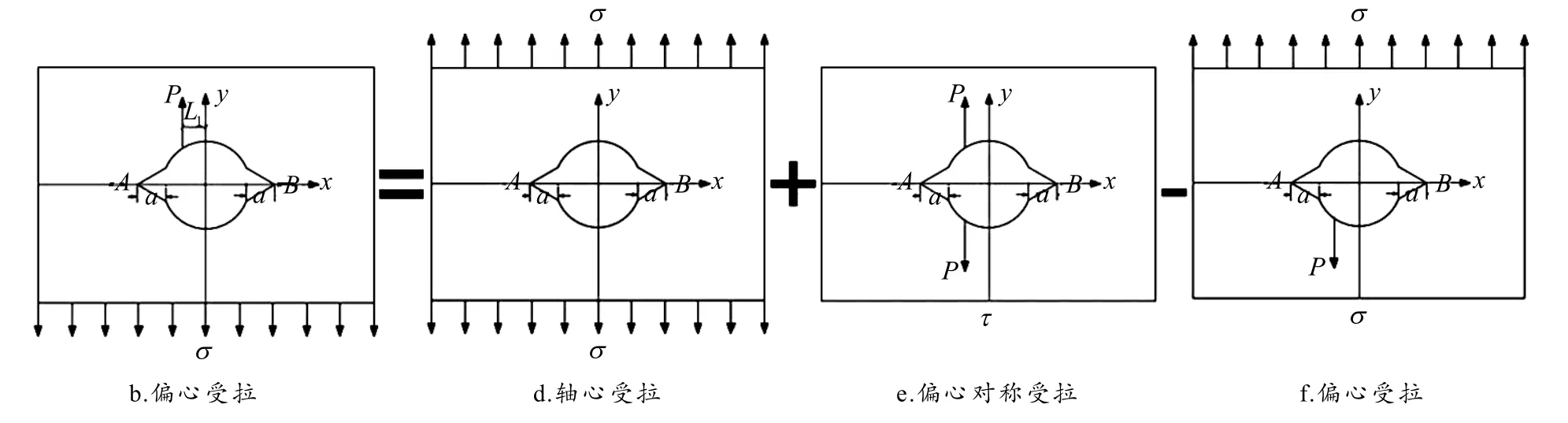
图4 铆孔偏心受拉分解示意图

应用叠加原理得到KbI表达式：

综合得到：

2 应用复变函数求解铆孔双耳裂纹尖端应力强度因子

2.1 应力强度因子的解析解

由式（5）及式（6）综合得到：

偏心作用下带双耳裂纹铆孔钢板，很难得到裂纹尖端应力场的精确求解.为了简化计算过程，将铆钉孔看做裂纹的一部分对裂纹尖端的应力强度因子进行分析，将含裂纹的符合广义胡克定律的钢板归结为弹性力学平面问题进行分析，寻找一个应力函数，使其满足边界条件要求的复变应力函数，即双调和方程.由文献[3]得到I/II复合型断裂破坏其应力强度因子的表达为：

其中φ′(z)为满足边界条件的应力函数.对于纯I型断裂破坏构建应力函数：

得到：

得到：

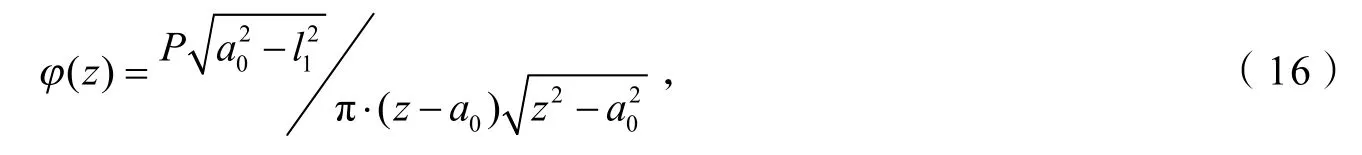
得到：

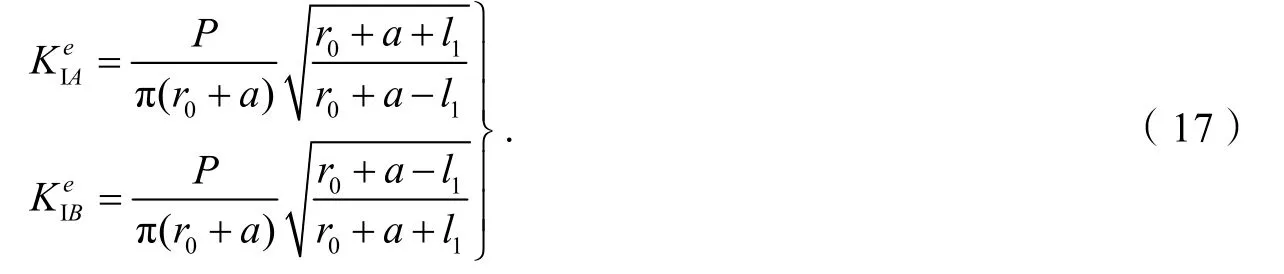
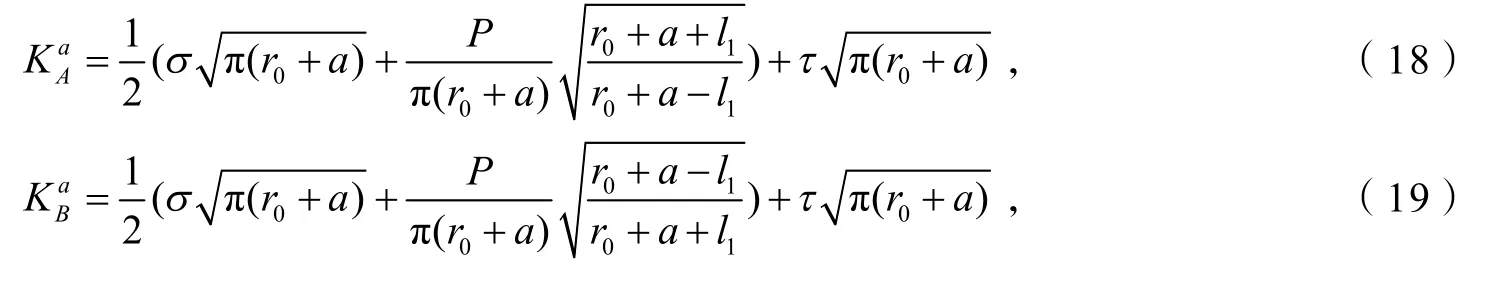
参考文献[3]算例得到中心受力双耳裂纹的K表达式：

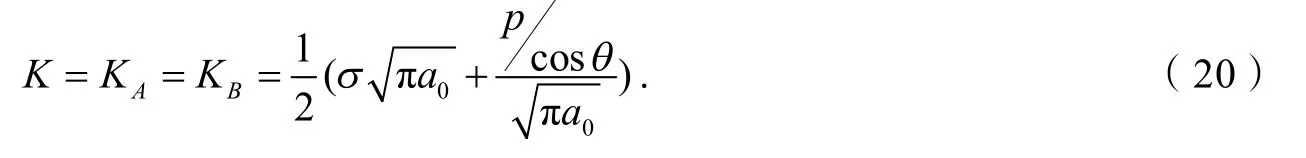
2.2 算例分析

以钢铆板铆孔直径20 mm、裂纹长度5 mm、受到集中力10 kN的板厚、板宽为无量纲单位1的钢板为例，以不同的偏心长度1l为变量，对比分析偏心作用下的铆孔双耳裂纹应力强度因子的变化特征.

表1 偏心与中心受力强度因子比值的变化特征

由表1可知，与中心受载情况下相比（90θ=°即中心受载），偏心作用时随着偏心距变小（θ变大）近偏心端（A端）在45θ=°时应力强度因子最大，对控制铆孔双耳尖端裂纹扩展越不利，应尽量避免；对于远离偏心端（B端），铆孔双耳尖端控制裂纹扩展随偏心距变小（θ变大）扩展越不利，但整体不超过对称受载，可以忽略.

3 结论

通过利用线弹性力学方法获得I/II型断裂破坏裂缝尖端的应力强度影子，应用叠加原理对偏心拉伸铆钉双耳进行静力学分析，并将其受力分解为简单的3部分，运用复应力函数得到各部分的解析解，最后分别得到双耳裂纹尖端/AB两侧解，通过与中心受载比较分析得到了偏心受力对控制近偏心端裂纹扩展不利，且偏心转角45θ=°时，应力强度因子达到最大；远离偏心端裂纹扩展可以忽略.实际工程中结构受力复杂，对于可能带裂纹工作的构件，设计过程中应适当增加安全系数，保证结构物使用安全；本文仅探讨了平面受力状态下偏心受力作用下的应力强度因子，对于空间结构受力对平面结构的影响将是下一步研究的方向之一.