基于Heston模型的期权隐含波动率研究

（广东农工商职业技术学院财经系，广东广州510507）

随着金融市场的不断发展，以期权为代表的衍生品成为了套利者和投机者最重要的资产配置工具.一个正常的市场应拥有价格的自发回归机制，使偏离的价格能回归到理性.要实现这一过程，投资者首先需要得到一个合理的价格作为参考.因此，如何利用理论模型计算期权等衍生品的合理价格，成为了维持市场理性的关键.Black-Scholes模型因其直观和计算简单为传统期权定价理论奠定了基础，但该模型的成立至少依赖于2个假设：一是标的资产的对数收益服从正态分布；二是基础资产的价格波动率为常数.但实际情况却并非如此，历史数据和实证研究表明：标的资产的对数收益具有超值峰度并呈负偏态分布，而非正态分布；基础资产的价格波动率会发生改变，且存在隐含波动率“微笑”现象.

为了使模型更贴近实际，1993年Heston利用随机波动率模型（包含5个参数，Ω={θ,κ,α,Vt,ρ}），并使用均值回复平方根描述了实时波动率方差，从而放宽了Black-Scholes模型的这两个假设.为考察 Heston模型的有效性，Melino等[1]通过研究外汇期权的定价，发现随机波动率模型优于 Black-Scholes模型.之后学者对 Heston模型的研究主要集中于两个方面：一是对模型参数的寻找；二是对模型的仿真求解.模型参数的寻找实质上是求组合最优的过程，传统的极大似然法中目标函数过于复杂，而且容易出现多个极值，难以准确求解，因此，有学者尝试了智能求解法：王林等[2]用模拟退火法估算模型参数，李斌等[3]用遗传算法求解模型参数.对模型仿真求解的研究主要是利用Monte Carlo加以实现，如Kahl[4]利用Monte Carlo方法对随机波动率模型的快速估算.

为验证Heston模型的有效性，本文首先假设一对固定的模型参数Ω={θ,κ,α,V0,ρ}={1.5,3,3,1,-0.5}；然后利用Heston模型推导隐含波动率计算公式，利用Monte Carlo分别得出标准的看涨期权和看跌期权的隐含波动率；最后将不同期限、不同行权价的期权对应的隐含波动率绘制在由期限、行权价和隐含波动率构成的三维坐标空间中，得出隐含波动率曲面.

1 模型与方法

1.1 Heston模型

Heston模型实际上是标的资产波动率符合CIR[5]过程的Black-Scholes SDE扩展形式.假设资产远期价格为Ft，随机方差为V，γt为常数，则Ft服从：

本文中，我们假设参数数值如表1所示.

表1 Heston模型参数假设

由于以上参数满足Feller条件[6]，因此Vt为正数.

1.2 隐含波动率的计算

当我们将一个已知到期日、行权价和市场价格的真实期权的参数带入到Black-Scholes模型后，其反解出的波动率即为隐含波动率.隐含波动率数值与Black-Scholes模型假设的常数波动率数值不同，理论上，其差别会随着到期日和行权价的变化而变化，并呈现出“V”字形“笑脸”状，故而又被称为期权隐含波动率“微笑”.这一过程可用公式表达如下：

其中，V表示期权的市场价格；VB-S为利用 Black-Scholes模型计算出的期权价格；K为期权的行权价；T为期权到期日；r为无风险利率；θimp为期权的隐含波动率，计算如下：

本文中，我们参考文献[3]的观点，用风险中性世界的期权价格代替现实世界的期权价格，并假设无风险利率r为0，方差V0为1，则隐含波动率是行权价K和到期日T的函数.为使研究更加直观和便利，我们将隐含波动率、行权价和到期日放在同一三维坐标里，进而得出隐含波动率曲面，

1.3 利用Monte Carlo估算隐含波动率

由于隐含波动率曲面是一个极其复杂和多变的系统，每一个模型参数的变化都会引起曲面的变化，难以穷尽计算.因而，我们考虑假设一组参数，并基于这组参数建立随机微分方程，然后使用Monte Carlo模拟对方程进行仿真估值.在本文中，隐含波动率是被建模对象，期权为标准化普通欧式期权.先将标的资产远期价格Ft对数化，并将这一过程用Xt表示，利用伊藤引理可以得出以下公式：

为模拟Xt和Vt，我们借助Euller[6]离散化方法得出：

其中，C与P分别表示看涨期权和看跌期权的价值，K为行权价，T为到期日，表示第i期的资产远期价格，而Xti的计算见式（7-8）.式（9）和式（10）利用Matlab最优化函数，假设行权价K=[ 0.7,1.3]和到期日T=[ 0.25,2]，通过反复模拟实现计算.最后将C、P作为期权市场价格带入Black-Scholes模型，利用式（4）反解出隐含波动率θimp.最终，我们可以得出以行权价K、到期日T为参数的隐含波动率面板.

2 实证结果

到期日T=2年，假设每天为一个交易日，可以得出504个离散点，利用Monte Carlo进行超过40000次模拟，可以分别得出看涨期权和看跌期权的隐含波动率面板.在面板中，我们假设坐标

2.1 看涨期权的隐含波动率面板

通过图1我们发现：看涨期权的隐含波动率会随着期权到期日和期权行权价的变化而变化，这一特点符合理论预期；右侧隐含波动率“微笑”大于左侧，这可能是由于 Heston模型参数中相关系数ρ假设为负数导致的；随着到期日的增加，隐含波动率“微笑”逐渐变平，这是由于均值回归速度κ使得θ均值回归；在较低的行权价和较高的行权价上，隐含波动率出现明显“上翘”，因为极端的行权价与标的资产的市场价严重脱钩时，人们会买入拥有较低行权价的看涨期货、卖出拥有较高行权价看涨期货，使得期权市场价格大幅波动，导致隐含波动率增加.

图1 看涨期权的隐含波动率面板

为进一步研究行权价与隐含波动率的关系，我们采用截面分析，绘制出短期（T=0.25）和长期（T=2）看涨期权的隐含波动率，并附带各自的置信区间，用于评估模拟的准确性，具体见图2.由图2可知：行权价越低，隐含波动率越高，但并未得出行权价越高，隐含波动率越高这一结论.在图2-a中，当期权行权价较高或较低时，隐含波动率曲线出现“上翘”，形成隐含波动率“微笑”；对比图2-b可知，这种“上翘”现象会随着期权到期日的延长而消失.

图2 看涨期权不同行权价下的隐含波动率曲线

2.2 看跌期权的隐含波动率面板

看跌期权的隐含波动率面板与看涨期权类似，具体见图3，不再赘述.

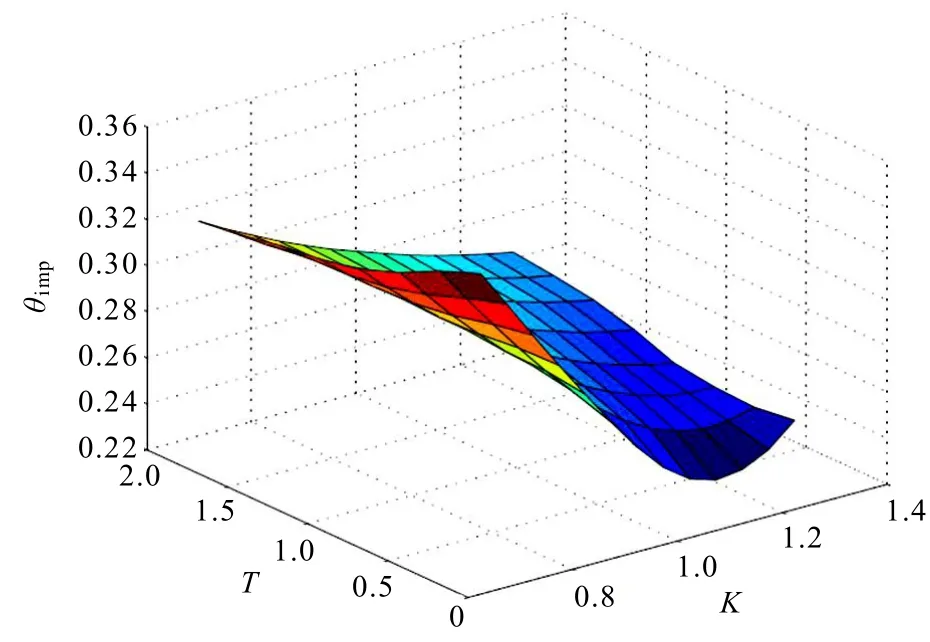
图3 看跌期权的隐含波动率面板

为进一步研究行权价与隐含波动率的关系，我们采用截面分析，绘出短期（0.25T=2）和长期（T=2）看跌期权的隐含波动率，并附带各自的置信区间，具体见图4.由图4，我们仍然可以得出“行权价越低，隐含波动率越高”这一结论；但不同的是，在图4-a中，右下角出现了“V”形特点，说明看跌期权行权价上升后，隐含波动率也上升.再次验证了在较低和较高的行权价上，隐含波动率出现明显“上翘”，形成隐含波动率“微笑”.这种“上翘”的现象会随着期权到期日的增加而逐渐消失.

图4 看跌期权不同行权价下的隐含波动率曲线

3 Heston模型参数的敏感性分析

为研究Heston模型参数与隐含波动率的关系，我们进一步设定如表2所示的3组情况，并以看涨期权为例依次作出隐含波动率面板图.

表2 Heston模型参数设定

3.1 θ敏感性分析

图5表明，当波动率长期均值θ增长时，隐含波动率曲面逐渐出现“下翻”；随着长期均值θ减小，隐含波动率曲面出现“上翻”.

图5 θ参数下的隐含波动率曲面

3.2 κ敏感性分析

图6中，随着均值回归速度κ的上涨，隐含波动率曲面“变平”的速度越来越快；当均值回归速度κ上涨到一定大小时，隐含波动率曲面的变化越来越小.

图6 κ参数下的隐含波动率曲面

3.3 α敏感性分析

图7表明，波动率方差α增加会使得隐含波动率曲面发生“上翘”；α越大，隐含波动率“微笑”越明显.

图7 α参数下的隐含波动率曲面

3.4 ρ敏感性分析

图8 ρ参数下的隐含波动率曲面

4 结论

本文的主要目的是使用 Heston随机波动模型改善 Black-Scholes模型关于对数正态分布和常数波动率的假设约束，使期权估价更加贴近实际.研究主要分为三大块：Heston随机微分方程的推导和利用，隐含波动率面板的建立与分析，以及 Heston模型参数敏感性分析.主要结论如下：1）看涨期权和看跌期权存在隐含波动率“微笑”；2）看涨期权和看跌期权的隐含波动率与行权价和到期日有关，当行权价很低或很高时，隐含波动率上升，并出现明显“上翘”，形成隐含波动率“微笑”，当到期日增加时，隐含波动率“微笑”消失；3）Heston模型参数的变化能直接影响隐含波动率的大小和形态.

标的资产的价格波动率是影响期权定价最重要的因素之一，基于Heston模型的期权隐含波动率的研究对指导期权定价具有重要意义.但本文也存在以下不足：1）对 Heston模型的应用基于一组假设参数，在对模型参数Ω={θ,κ,α,ρ}进行敏感性分析时，我们假设无风险利率为 0，方差为 1，这不一定符合实际情况；2）在将微分方程转化为差分方程时，未对可能为负的方差项Vt进行特殊处理，本文借助了Euler法，而没有比较和讨论IM和FT等其他方法；3）在运用Monte Carlo模拟期权估值时过于简单，没有加入控制变量以提高预测准确性.