抛物线y=ax2+bx+c一条鲜为人知的性质

云南省昆明市宜良县职业高级中学(652100) 胡光明

对于抛物线y=ax2+bx+c,老师们一般只关注对定义(一般式、顶点式、交点式)、图像(画法)、一般性质(定义域、值域、开口方向、顶点坐标、对称轴、增减性、最值)及应用等内容的研究,很少注意更广泛的开拓性研究.

在教学中,笔者发现,抛物线y=ax2+bx+c还有一个很有趣的性质,写下来与同仁分享.

定理抛物线y=ax2+bx+c上依次取不重复的四个点,若第一点与第二点、第三点与第四点横坐标间距相等,则这四点构成的四边形是梯形,其两底的比值为定值.

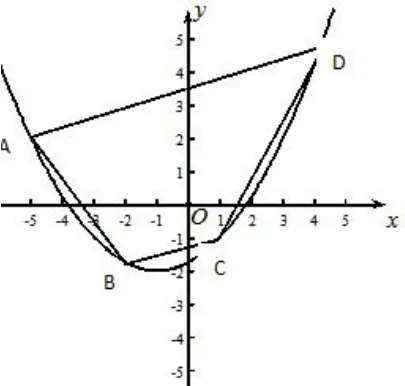
图1

如图1,已知抛物线上四点A、B、C、D,A点和B点横坐标的间距与C点和D点横坐标的间距相等.求证:四边形ABCD为梯形,且为定值.

推论1抛物线y=ax2+bx+c上依次排列的四个点,若相邻两个点之间横坐标间距相等,则这四个点构成的四边形是梯形,其两底的比值为3.

推论2抛物线y=ax2+bx+c上依次排列的四个点,若相邻两个点之间横坐标间距都是1,则这四个点构成的四边形是梯形,其两底的比值为3.

这一定理在解一些相关联的题目时,有化难为易的功效,举例如下.

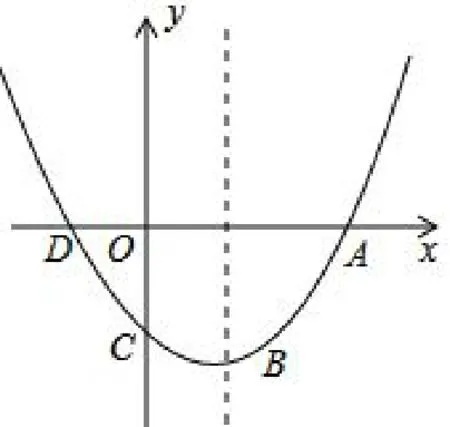
图2

例1如图2,已知抛物线与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.

(1)直接写出A、D、C三点的坐标;

(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;

(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.

这是2014年广东省汕尾市的一道数学中考题(第25题),有一定难度.一般思路和解法摘录如下.

分析(1)令y=0,解方程可得到A点和D点坐标;令x=0,求出y=−3,可确定C点坐标;

(2)根据抛物线的对称性,可知在在x轴下方对称轴右侧也存在这样的一个点;再根据三角形的等面积法,在x轴上方,存在两个点,这两个点分别到x轴的距离等于点C到x轴的距离;

(3)根据梯形定义确定点P,如图所示:[1]若BC//AP1,确定梯形ABCP1.此时P1与D点重合,即可求得点P1的坐标;[2]若AB//CP2,确定梯形ABCP2.先求出直线CP2的解析式,再联立抛物线与直线解析式求出点P2的坐标.

解(1)因为,所以当y=0时,解得x1=−2,x2=4.当x=0,y=−3.所以A点坐标为(4,0),D点坐标为(−2,0),C点坐标为(0,−3);

[1]点M在x轴下方时,根据抛物线的对称性,可知点M与点C关于直线x=1对称,因为C点坐标为(0,−3),所以M点坐标为(2,−3);

[2]点M在x轴上方时,根据三角形的等面积法,可知M点到x轴的距离等于点C到x轴的距离3.当y=3时,,解得,所以M点坐标为.综上所述,所求M点坐标为(2,−3)或;

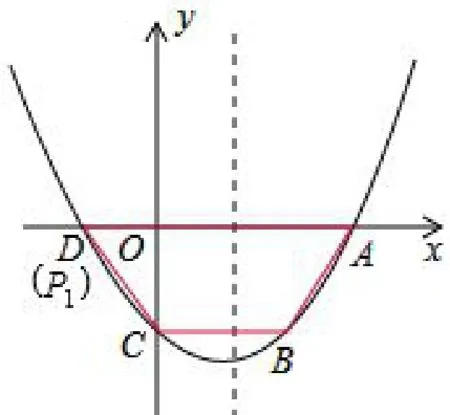
图3

(3)结论:存在.如图3所示,在抛物线上有两个点P满足题意:[1]若BC//AP1,此时梯形为ABCP1.由点C关于抛物线对称轴的对称点为B,可知BC//x轴,则P1与D点重合,所以P1(−2,0).因为P1A=6,BC=2,所以,所以四边形ABCP1为梯形;

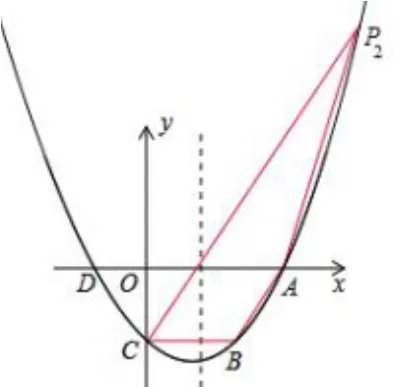
图4

[2]若AB//CP2,此时梯形为ABCP2.因为A点坐标为(4,0),B点坐标为(2,−3),所以直线AB的解析式为y=所以可设直线CP的2解析式为将C点坐标(0,−3)代入,得n=−3,所以直线CP2的解析式为因为点P2在抛物线上,所以,化简得:x2−6x=0,解得x1=0(舍去),x−2=6,所以点P2横坐标为6,代入直线CP2解析式求得纵坐标为6,所以P2(6,6).因为AB//CP2,AB̸=CP2,所以四边形ABCP2为梯形.

综上所述,在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(−2,0)或(6,6).

上述第三个问题的解答颇花费了一些笔墨.若应用本文定理,就来得容易多了.

事实上,已求出C、B、A三点的坐标分别为C(0,−3)、B(2,−3)、A(4,0),因为C、B、A这三个点横坐标间距都是2,根据上述定理及推论,P点与C点横坐标的间距或P点与A点横坐标的间距为2时,四边形ABCP为梯形.所以P点的横坐标应为−2或6,于是得点P的坐标为(−2,0)或(6,6).

例2已知对任意实数x,二次函数f(x)=ax2+bx+c恒非负,若a＜b,求的最小值.

对于本题,《数学通报》2012年第12期的文章《回归知识基础 关注基本性质》有过精彩的讨论.通过阅读文[1],笔者了解到《数学通报》2008年第12期、2010年第9期也有文章研究过此题.

这里,笔者仅从本文定理及推论的角度,对例2进行讨论.

通过观察,结合二次函数f(x)=ax2+bx+c相关知识易知:f(−1)=a−b+c;f(0)=c;f(1)=a+b+c.这些信息均与解题目标相关,而它们相应的点的横坐标间距都是1,且f(0)−f(−1)=b−a,因此考虑引入第四个元素f(−2),使以横坐标为-2、-1、0和1的四个点满足构成梯形的条件 (推论 2).由f(1)−f(−2)=3[f(0)−f(−1)]得:a+b+c−f(−2)=3(b−a),即:,因为对任意实数x,二次函数f(x)=ax2+bx+c恒非负,所以f(−2)≥0,又因为a＜b,所以当且仅当f(−2)=0时等号成立.由知,b=c=4a.问题迎刃而解.

其实,围绕本文定理及推论,仿照例2可以得到一系列翻版或升级版的命题.比如:

(1)已知对任意实数x,二次函数f(x)=ax2+bx+c恒非负,若25a+5b＞0,求的最小值.

(2)已知对任意实数x,二次函数f(x)=ax2+bx+c恒非负,若b＞3a,求的最小值.

(3)已知对任意实数x,二次函数f(x)=ax2+bx+c恒非负,若b＞2a,求的最小值.

(4)已知对任意实数x,二次函数f(x)=ax2+bx+c恒非负,若3a+b＞0,求的最小值.

不胜枚举.

本文提出的抛物线内接梯形的原理,还可应用到抛物线作图上.取抛物线上横坐标间隔距离相同的三个点(最好是先定出顶点),即可通过推平行线的方法分别向两侧找到第四点、第五点……,从而作出抛物线的图像.读者可自行尝试,这里不再赘述.