巧设空间形式 突显直观想象—以近三年高考全国卷立体几何选填题为例

广东省深圳市龙华区教育科学研究院(518029) 殷木森

高考试题逐渐由“能力立意”转为“素养立意”是大势所趋,从近几年的高考全国卷试题可以看出,命题者正在不断地探索试题如何体现“素养立意”.而“直观想象”是高中数学六大核心素养中唯一新造名词,《普通高中数学课程标准(2017版)》是这样描述的:直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决问题的素养.笔者认为,主要包含两点:一是要发展几何直观与空间想象能力,建立数与形的联系;二是能通过分析与想象,思考和解决具体问题,在具体事物中感悟事物的本质.可见,“直观想象”素养对考生的要求很高,能充分体现数学试题在高考选拔中的特殊作用,命题者理应会非常关注这一素养.

通过研究近三年全国卷试题发现,以立体几何知识为载体的选填题,特别是选择题第11、12题,填空题第16题,需要考生巧妙构造空间几何形式,充分体现“直观想象”立意,考查创新意识和实践能力.以下是笔者的一些分析与思考,不当之处,敬请批评指正.

一、借助正方体,巧设线面间位置关系

正方体由于各条棱长度相等,且有三组棱分别平行,是三维空间中极为对称的图形.若再引入另一个截面,构造棱与截面所角的角,截面与正方体其它线面所成的角,便能在不同水平考生的脑海中出现不同的空间几何形式,区分的效果非常明显.

例1(2018年全国I卷,理科第12题)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )

分析此题是一道改编题.原题要求正方体十二条棱与某一截面所成角相等时求该角的三角函数值,而本题则改成求满足条件的截面中,面积最大的一个,反其道而行之.为此,分两步进行求解:

第一步:找出符合条件的其中一个截面.如图1,在正方体ABCD−A1B1C1D1中,把十二条棱分成三组,即只需要同一顶点出发的三条棱与截面所成的角相等即可, 如以A 顶点出发的三条棱,容易找到截面A1BD,其面积为.这是截面面积最大的吗?显然不是.

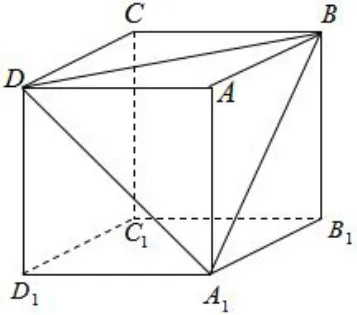
图1

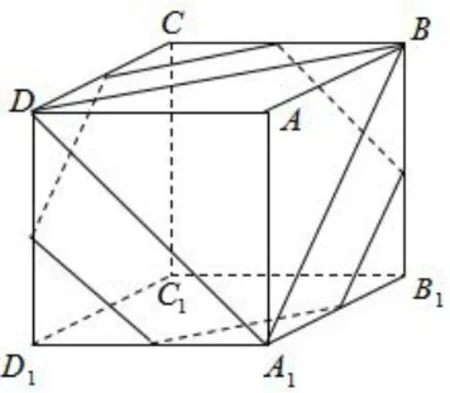
图2

第二步:找与截面A1BD平行的截面中面积最大的一个.当平行截面往A顶点靠近时,面积显然变小;所以平行截面只能往下移,变成一个六边形,其面积逐渐增大,当截面与各边的中点相交时,截面变成一个正六边形,此时面积最大,如图2,因为由正方体的对称性可知,当平行截面再往下移时,面积则又会逐渐减小至(△CD1B1的面积).所以最大值为,选A.

反思本题深刻反映了高考命题的方向“多考一点想,少考一点算”,在第二步中,若考生通过构造函数求最大值,即先把六边形的面积表达成函数关系式,再求函数的最大值,而不是通过分析思考的方法,则会“小题大做”,违背命题者的本意.

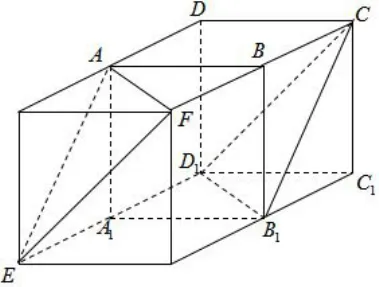
图3

例2(2016年全国I卷文理科第11题)平面α过正方体ABCD−A1B1C1D1的顶点A,α//平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )

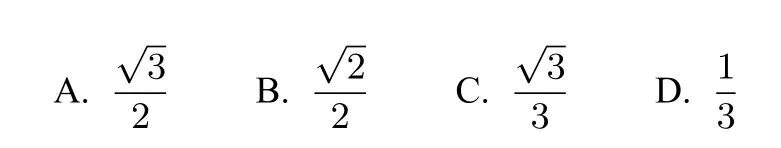
分析此题是一道漂亮的原创题.考生自然会问:平面α究竟在哪?m,n所成角其实可以等价为哪个角?不同水平考生的理解肯定不一样.为此,可以逐步进行分析与解决:

最初想法:先过点A如何作出平面α.只能补一个相同的正方体,如图3,过点A的平面AEF就是平面α,m=AF,由面面平行的性质定理可得EF//n,所以∠AFE就是m,n所成的角,正弦值为

进一步思考:还有没有更简洁的解法?

我们会发现,其实不补形也行,因为平面A1BD//平面AEF,而平面A1BD//平面CB1D1,平面CB1D1∩平面A1B1C1D1=B1D1,平面CB1D1∩平面C1CDD1=CD1,由面面平行的性质定理可知∠CD1B1就是m,n所成的角,其正弦值为,选A.

反思本题的平面α按常规方法确实难找,“不识庐山真面目,只缘身在此山中”是此题的真实写照.仔细一思考∠CD1B1就是m,n所成的角,因为α//平面CB1D1,只需由面面平行的性质定理得出即可.但要分析思考出来,没有相当的直观想象,恐怕难以成行.

二、借助锥柱体,巧设动态几何体积

锥柱体内接或内切另一个几何体,或是动态的锥柱体,这样构成的空间几何形式,由于其不定性,同样是体现直观想象的最佳载体.

例3(2016年全国III卷文科第11题)在封闭的直三棱柱ABC−A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是()

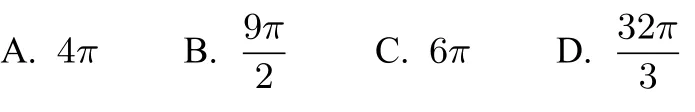
分析此题是一道原创题.我们只需要弄清两个问题:

1.这个直三棱柱是怎样的?

由AB⊥BC,AB=6,BC=8得知底面△ABC是一个直角三角形,所以这个直三棱柱其实是长方体的一半(图略).

2.内切球怎样与直三棱柱的面相切?

最理想的状况是球与底面、侧面均相切.分两种情况:一是当球与两底面相切,此时球的半径为;二是当球与三个侧面相切,球的半径为2.比较得知只能是第一种情况.选B.

反思本题虽说落脚点并不难,应先迅速得出该直三棱柱其实是长方体的一半,但若困域于空间形式的复杂性时,考生将无从下手.故此,本题很好地反映了此类题型“空间想象”是起点,而“分析解决”是落脚点.

例4(2017年全国I卷理科第16题)如图4,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB,分别是以BC,CA,AB为底边的等腰三角形,沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为____.

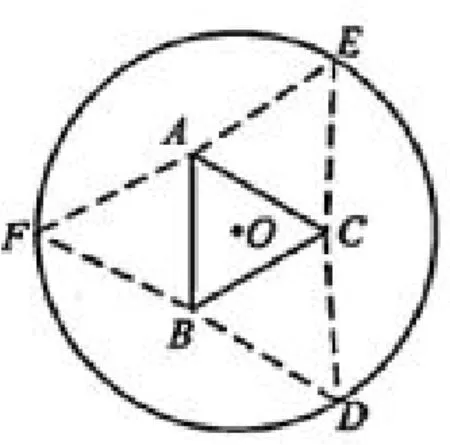
图4

分析本题是一道漂亮的改编题.等边三角形ABC的中心O就是圆O的圆心,△ABC的大小可以改变,极限的情况就是圆O是△ABC的外接圆,但此时折起并不能得到三棱锥.故可设△ABC的内切圆的半径为x,则三个等腰三角形底边上的高为5−x,若能折起得到三棱锥,则5−x＞x,即.为此,要解决两个问题:

1.三棱锥体积的函数表达式怎样?

反思本题通过空间想象,得到一个动态的正三棱锥,当底面积增大时,高必然减小,故“设△ABC的内切圆的半径为x”是关键一步,然后构造函数借助导数求最值.若考生不能通过想象得出三棱锥各边的关系,本题的解答亦会相当艰辛.

三、借助旋转体,巧设线线位置关系

虽然高中阶段只要求学习简单的旋转体,如圆柱、圆锥、球等,但是通过它们的外接或内切几何体,构造动态空间几何形式,或者再外设线、面,使其与旋转体的母线、高等构成动态的角、面,对考生的挑战同样很大.

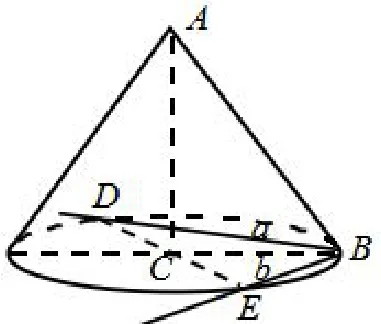
图5

例5(2017年全国III卷理科第16题)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:

[1]当直线AB与a成60°角时,AB与b成30°角;

[2]当直线AB与a成60°角时,AB与b成60°角;

[3]直线AB与a所成角的最小值为45°;

[4]直线AB与a所成角的最小值为60°;其中正确的是____.(填写所有正确结论的编号)

分析本题是一道原创题.较之前面几题,本题起点更高,即题目给出的空间几何形式究竟是怎样的?考生一时不能难以确定.此时,我们只能一步一步来,先确定最关键的元素—圆锥,再思考其它元素,如两条互相垂直的直线a,b究竟在哪更为合适.由于边AC所在直线与a,b都垂直,所以不妨设a,b都在底面上,DE为底面圆C的直径,连结BD、BE,设BD为a,BE为b,因为a⊥b,如图5.易知直线AB与a所成角的最小值为45°,选[3];设BC=x,则,当直线AB与a成60°角时,,又因为DE=2x,所以,即AB与b成60°角,选[2].

反思本题若能通过直观想象得出图5,则成功了一大半,若再能把[3]选出,则就能完全猜出答案是2[3]○,因为当直线AB与a所成角的最小值为45°,a,b在同一底面上,所以AB不可能与b成30°角,故[1]有误,[2]正确.

以素养立意命制的题目,思维的含金量一定会更高一些,题目的入口也会更窄一些.其实本题的意思很简单:已知一圆锥的轴截面是等腰直角三角形,a,b是其底面上两条相互垂直的两条直线.当母线AB与a成60°角时,求AB与b所成的角.但如果这样命题,就会失去很多意义,只能考查考生简单的数形转换能力.

笔者相信,通过“巧设空间形式,突显直观想象”的试题在未来的高考中一定会有更重的份量,因为这是体现数学核心素养“可测”的一种重要方式.