本质回归 让一次“邂逅”不再陌生—探究2018年高考新课标卷理科第21题

广东省广州大学附属中学(510050) 韩智明 陈经纬

题目1(2018年高考新课标卷I理科第21题)已知函数

(1)讨论f(x)的单调性.

(2)若f(x)存在两个极值点x1,x2,证明:

分析我相信广大考生看到此题,应该有一种似曾相识的感觉,感觉它就是不久前的一次邂逅和相识,但回忆起来又是那么的模糊,特别是对第(2)问大多数考生一动起笔时总感觉缺少一种关联,总是出现思维链条的断裂;还有一部分考生虽然按照分析法的解题思想处理成功,但是很多同学还是不明白其中的原理.

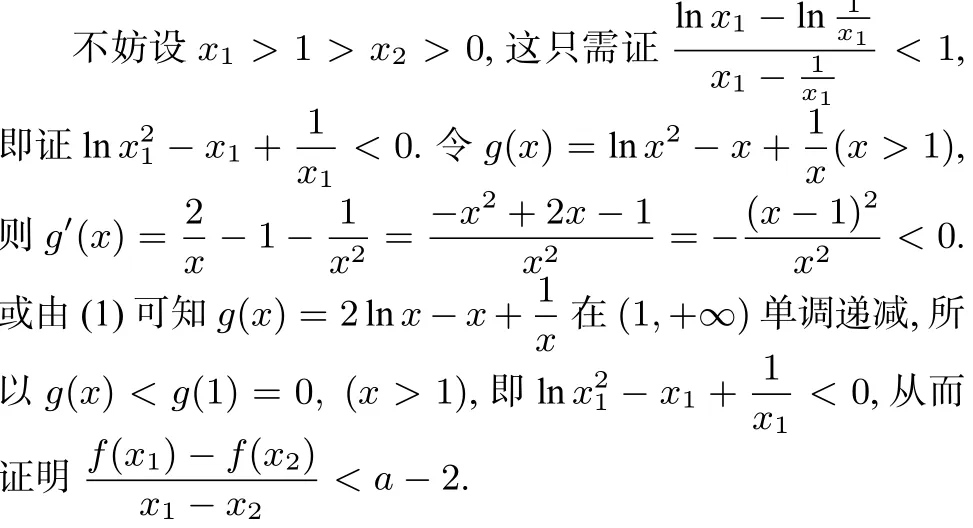
点评笔者认为如上方法为本题的最佳解法.通过极值点找出两根x1,x2的关系x1x2=1,再通过把要证明的不等式通过减少变量化为一元变量不等式,构造函数然后证明不等式即可.考生只有经过这种数学思维和方法的训练,才能想到这种方法,本题充分体现了数学逻辑推理的核心素养.

无独有偶,在以往的高考试题中也出现类似的情况.

题目2(2011年全国高考湖南卷文科第21题)设函数

(1)讨论f(x)的单调性;

(2)若f(x)有两个极值点x1,x2,记过点A(x1,f(x1)),B(x2,f(x2))的直线的斜率为k,问:是否存在a,使得k=2−a.若存在,求出a的值,若不存在,请说明理由.

分析此题虽然和题1题干有所不同,但究其本质应该是相同的,可见高考考查考生的数学思维的思想和本质不变,具有较为稳定的连续性.

点评题1和题2的解法相似,也是它们共同的最佳的解法,但针对不同形式但本质相似的试题,我们在教学中可以探究此类数学问题的其它的具有共性的解决方法,也就是回归此类题目解法的本质.

本质回归当大家看到题目1和题目2的解法以后,熟知其本质就是充分挖掘题目隐含条件,变二元变量问题为一元变量问题,我们原本模糊的感觉应该变得越来越清晰了,以往在平时的备考中众多的“邂逅”一下子变得深刻,我们可以感受到函数与导数的制题都有一个背景和平台,这个背景和平台隐藏在平时的练习和教材中,它可以是教材中典型问题的变式,或是经典问题的引申,这些已经成为压轴题命制的一个重要手段和特征,这些背景和平台对于考生来说可能是一次偶然的遇见,或是多次没有多少印象的邂逅,亦或从来都没有见过.理解和掌握这些背景知识,无疑会有助于我们迅速找到解决问题的切入口.

分析第(2)问从问题的形式上,所求证的不等式存在三个变量a,x1,x2,让人难以入手,通过分析法思想经过逻辑推理不等式成立所需要的条件,然后通过换元减少变量达到求解目的.

点评两种解法对变量a处理的的方式稍有不同,但它们的思维起点一样,通过逻辑推理变形化多元变量为一元变量,最终转化为函数问题解决,思维导向明确,极大地体现了学生的数学运算、处理数学问题等学科核心素养.

在近几年的高三模拟题中,时常出现一类给出函数图像上任意两个不同点的坐标,考察过两点的割线的斜率与图像上某点处切线斜率之间大小关系的函数综合问题,这类问题由于含有多个变量,显得非常复杂,同时还常有参数在内搅局,更使问题增添许多混乱.

题目4(2014年江西师大附中高三期中考试)已知函数f(x)=lnx+ax2+x.

(1)若f(x)在(0,+∞)是增函数,求a的取值范围;

题目5(2018年黄冈中学模拟试题)已知函数f(x)=

(1)若直线x=t(t＞0)与曲线y=f(x)和曲线y=g(x)分别交于A,B两点,且曲线y=f(x)在A处的切线与y=g(x)在B处的切线相互平行,求a的取值范围;

(2)设h(x)=f(x)−g(x)在其定义域内有两个不同的极值点x1,x2,且x1＞x2.已知λ＞0,若不等式恒成立,求λ的取值范围.

分析第(2)问中从给出的不等式中含有三个变量,通过对不等式e1+λ＜x1·xλ2两边取对数等价转化为1+λ＜lnx1+λlnx2,消去变量a,得到含有变量x1,x2的不等式,然后通过变形换元将二元问题化为一元问题,转化为函数问题解决.

(2)若λ2＞1时,当t∈(1,λ2)时,φ′(t)＜0;当t∈(λ2,+∞)时,φ′(t)＞0.所以φ(t)在 (1,λ2)上单调递减,在(λ2,+∞)上单调递增,又φ(1)=0,所以φ(x)在(1,+∞)上不能恒小于0,不符合题意,舍去.

综合(1),(2)得,若不等式e1+λ ＜x1·xλ2恒成立,只须λ2≤1.又λ＞0,所以0＜λ≤1.

点评题4和题5都含有三个变量,其解法是解决此类数学问题的常规策略,其思路就是通过消元、换元不断减少变量的个数,使之转化为我们熟知的一元函数,最后利用导数证明不等式,解题过程中所蕴含的解题思想都是化多元变量为一元变量的本质回归.

初看2018年高考新课标卷理科21题,也许会有人会提出该题作为压轴题的质疑,认为它的难度和创新不够,不符合大众对压轴题认识的某种心理,然而笔者通过对该题的解法和命题背景分析来看,特别是在新高考改革即将实施的大背景下,越发感觉广大的数学专家、教育专家及测评与评价专家通过对新课标十年的论证和摸索已经形成了自己的命题风格:平和—表述简明,言简意赅;稳定—平稳过渡,风采依旧;独特—背景深刻,韵味无穷.

21题作为压轴题难度的适当降低显然预示着已经开始为未来的文理高考合卷拉开序幕,悄然指明今后高考备考的方向;通过本题的解法研究要求我们在整个复习备考中,特别是在教学活动中,教师要加强对数学问题的探究性教学,重视变式训练,注重对同一个习题多个知识点的改编、重组和变式,训练和优化学生的思维品质,不要就题论题,通过教学活动让学生对问题进行多角度、多层次(问题正反面、问题的纵横向、问题的特殊和一般)的拓展和探究,学生在解决数学问题时能够举一反三,会思考、会拓展;树立备考以提升学生数学学科核心素养为出发点,全方位地培养学生的综合处理数学问题的能力,落实在每一堂课里,渗透到每一个习题中,让学生在教学活动中体验数学活动经验,掌握数学本质,感受数学思想,学会数学地思考问题,培养学生思维的灵活性和深刻性;在解题活动中要注重知识的梳理总结,理解解题方法的本质,形成对一类试题解题共性的本质核心归纳和方法提升,加强学生的数学学科核心素养的培养,远离题海训练,用数学的眼光观察、分析和解决问题,高考呼唤数学本位的灵魂回归,备考急需数学思想的本质回归,学生只要掌握理解了知识方法的本质所在,哪怕是与相关试题的一次“邂逅”甚至没有遇见,也不会感到陌生.