2018年高考全国I卷解析几何题的探究与推广

广东省湛江一中培才学校(524037) 魏欣

广东省雷州市第八中学(524232) 邓春梅

一道高考解析几何试题的命题背景可能就是圆锥曲线的一个性质定理的特殊情况.如果掌握了定理的原理,也就把握了试题的本质.对一些典型的试题,不应满足于会解,可以引导学生深入探究试题背后的知识背景,挖掘问题的本质.这样才能真正找到解决问题的方法,学会用更高观点去看待数学问题,把握问题的本质.正如《普通高中数学课程标准(实验)》所倡导的数学探究性课题学习,引导学生围绕某个数学问题,观察分析,自主探究,提出有意义的数学问题,探求适当的性质结论或规律.以下是引导学生从2018年高考全国I卷解析几何题出发,探究圆锥曲线的性质,揭示问题的本质.

一、试题展示

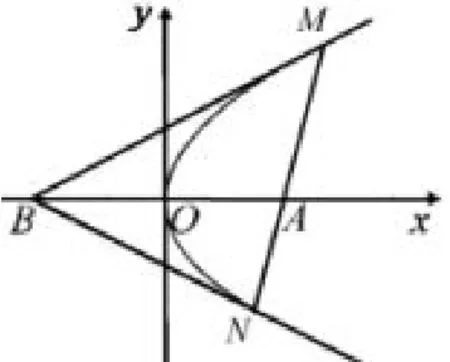
图1

题目1(2018年高考全国I卷文科第20题)如图1所示,设抛物线C:y2=2x,点A(2,0),B(−2,0),过点A的直线l与C交于M,N两点.

(1)当l与x轴垂直时,求直线BM的方程;

(2)证明:∠ABM=∠ABN.

解(1)当l与x轴垂直时,l的方程为x=2,可得M的坐标为(2,2)或(2,−2).所以直线BM的方程为或

(2)(i)当l与x轴垂直时,AB为MN的垂直平分线,所以∠ABM=∠ABN.

(ii)当l与x轴不垂直时,设l的方程为x=ky+则x1＞0,x2＞0.由2消去x,得y−2ky−4=0,所以

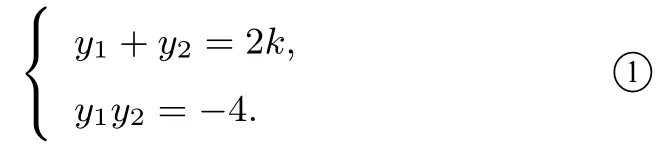
直线BM,BN的斜率之和为

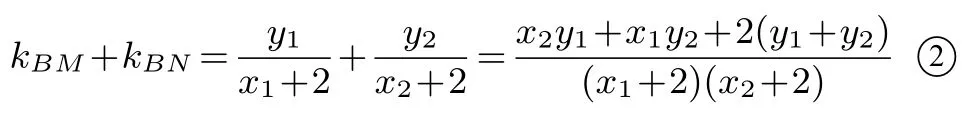
将[1]式和x1=ky1+2、x2=ky2+2代入[2]式分子,可得

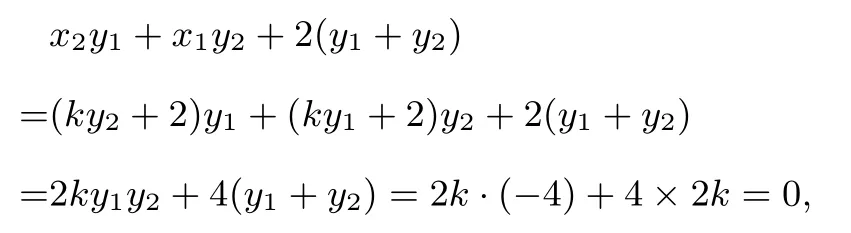
所以kBM+kBN=0.可知直线BM,BN的倾斜角互补,所以∠ABM=∠ABN.

综上所述,∠ABM=∠ABN.

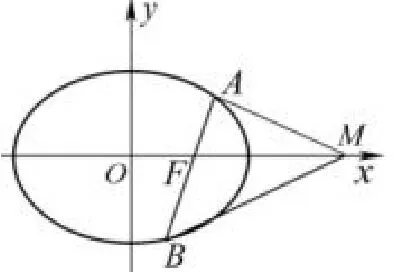
图2

题目2(2018年高考全国I卷理科第20题)设椭圆的右焦点为F,过F的直线l与C交于A,B两点,点M的坐标为(2,0).

点评以上两题是2018年高考全国I卷的倒数第二题,是选拔题.第(1)问根据直线方程的求法,多数学生都能完成,第(2)问是个探索性问题,重点考查用坐标法研究圆锥曲线中的定点定值问题,考查数形结合、函数方程、分类讨论等基本数学思想,同时考查综合运用所学数学知识分析问题和解决问题的能力,综合考查学生的运算能力和数学素养.本题的呈现形式“平易近人”,是平几中的角平分线问题,但本题的解决过程却充分体现了坐标法的思想,可以将等角的几何关系式转化为坐标代数关系式,然后再用坐标法来处理.本题看起来很平常,实际上却背景丰富,有一定难度和区分度,也有很大的教学价值和研究空间,下面重点研究第二小问的相关性质.

二、性质研究

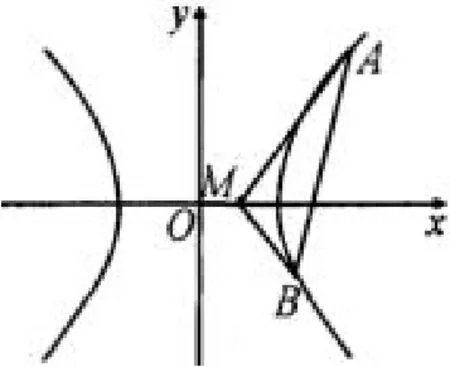
图3

性质3的证明与性质2的证明相仿,篇幅关系,此处不再赘证.

三、性质推广

图4

性质6已知抛物线y2=2px(p＞0)及A(m,0)、B(−m,n)(其中),直线l过点A且与抛物线交于不同的两点P、Q,设直线PB、AB、QB的斜率分别为kPB、kAB、kQB,则kPB+kQB=2kAB.

性质5、性质6的证明与性质4的证明相仿,篇幅关系,不再赘证.

四、真题回顾

由以上性质不难发现,在2015年全国I卷理科第20题、2015年北京卷理科第19题、2015年四川卷理科第20题、2013年陕西卷理科第20题、2010年全国卷I理科第21题、2008年福建卷文科第22题,也均以上圆锥曲线的性质,体现了高考试题“常考常新,推陈出新”的理念.均可以用上述的通性通法来解答,由于篇幅关系,此处之作简析.

1.(2015年高考全国I卷理科第20题)在直角坐标系xOy中,曲线与直线交与M、N两点.

(I)略;(II)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.

简析(II)由性质1易得直线l过y轴上的定点P(0,−a).

(I)略;(II)设O为原点,点B与点A关于x轴对称,直线PB交x轴于点N.问:y轴上是否存在点Q,使得∠OQM=∠ONQ?若存在,求点Q的坐标;若不存在,说明理由.

简析(II)由性质2易得,点Q的坐标为或

2.3 疗效判定 治疗前，两组患者视力水平无显著性差异，经过3周临床连续性静脉注射前列地尔治疗后，治疗组有效率显著高于对照组(P＜0.05）(见表 3）。

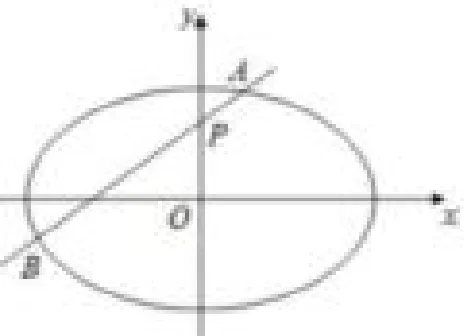
图5

(I)求椭圆E的方程;

(II)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使得恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.

简析(I);(II)由性质2可知,存在点Q(0,2),使得恒成立.

4.(2013年陕西卷理科第20题)已知动圆过定点A(4,0),且在y轴上截得的弦MN的长为8.

(I)求动圆圆心的轨迹C的方程.

(II)已知点B(−1,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P、Q,若x是∠PBQ的平分线,证明直线l过定点.

简析(I)y2=8x;(II)类比性质2易得,直线l过定点(1,0).

5.(2010年全国卷I理科第21题)已知抛物线C:y2=4x的焦点为F,过点K(−1,0)的直线l与C相交于A、B两点,点A关于x轴的对称点为D.

(I)证明:点F在直线BD上;(II)略.

简析由条件知焦点F(1,0),点A、D关于x轴的对称,直线BD不与x轴垂直,类比性质1可得,直线BD过焦点F在直线BD上.

6.(2008年福建卷文科第22题)已知椭圆C:的一个焦点为F(1,0),且椭圆过点(2,0).

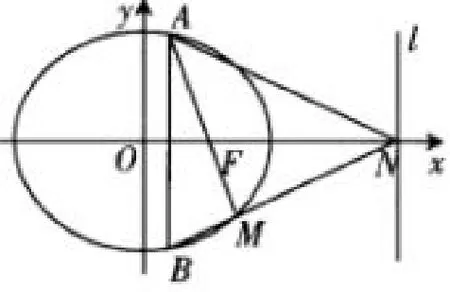
图6

(I)求椭圆C的方程;

(II)如图6,若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.

(1)求证:M点恒在椭圆C上;(2)略.

简析(I)求得椭圆C的方程为

(II)(1)点N的坐标为(4,0),易得设直线BN与椭圆C交于另一点M1,由AB为垂直于x轴的弦知点A、B关于x轴对称,则直线AM1不与x轴垂直.由性质4可得,直线AM1过焦点F(1,0),即直线AF过点M1,又由条件知直线AF过点M,且M、M1都在直线BN上,则点M、M1重合,故点M恒在椭圆C上.

五、备考建议

1.解析几何的核心方法是用代数的方法研究几何问题.在解题过程中,首先要将文字信息、图形条件进行转换,通过代数语言描述几何要素及其关系,将已知的几何条件表示成代数式,然后进行适当的代数运算得出代数结果,最后通过分析代数结果的几何含义解决几何问题.在这个过程中要经历文字信息、图形特征和符号语言之问的多重转换,因此,我们必须重视对几何关系的深入研究,探究用何种代数形式能恰当表示题目中的几何关系,同时有利于代数运算,从而形成正确的解题策略.

2.重视解析几何的运算教学.“不会运算、运算出错”是高中数学学习的普遍现象,解析几何更是如此,很多问题学生不是不会做,他们运算能力太差,就是算不出结果或者算错,因此,教学中要利用好学生的错误运算资源,剖析失误的原因,加强“算理”的分析.

3.充分发挥历年高考题的教学功能.首先教师所选择的历年高考题要有典型性,课堂上通过历年高考题的教学,要能辐射到多种思想方法,或能起到构建知识框架的作用,或能揭示一般性的解题策略等等,从而达到教学效果的最大化,是解题教学的理想境界.

4.课堂例题要少而精.选择少而精的例题能减少学生思维的断层,教师可通过探究、变式、一题多解等手段,来加强学生思维的连续性,从而调动学生的学习积极性.这就需要我们教师在选题上下功夫,在例题的解题教学分析上下功夫,找准课堂的主攻方向,是通过问题探究激发学生的兴趣,还是通过一题多解构建思想方法,或是通过问题回顾来还原知识体系等等.

5.加强解题后反思,进一步发展思维和提升能力.圆锥曲线的定点、定值和定直线等探索性问题历来是高考命题中的一个热点,此类问题往往蕴含具有代表性、引申性的数学知识、性质.由一个问题往往能引申出多个结论.它的延伸、推广,可以呈现出丰富多彩的数学内容.因此,在平常备考时,我们要有意加强对圆锥曲线性质的推导与证明,注重对历年高考题进行适当的发散研究,可以让达到深化认识、举一反三的目的,使得我们在高考中就能快速作答.另外,对于培养学生发展思维、创造性品质也有着重要的意义.