探究递归思想 提高学生计算思维能力

李海磊

（江苏省南通市海门市海门中学，江苏海门 226100）

引 言

人工智能的快速发展已经越来越多地影响着我们的生活，抢占人工智能发展的制高点关乎国运及民族未来。我国人工智能最后能发展到什么样的高度，取决于我们能培养和发展出什么样的人才。

中学阶段的信息技术教学必须能够围绕这个大目标，紧随时代发展的需要，积极改革。2010年，陈国良院士在一次报告中提出的“计算思维培养”应该作为计算机基础课程教学改革的一个重点。因此，信息技术课堂在教授学生基本技能的同时，更要把培养学生的计算思维置于一个前所未有的高度。中学生计算思维的培养不能只停留在口号上，而应该从课上课下的每一个概念、算法、程序细节的讲解和训练等方面入手，夯实基础，一步一个脚印、踏踏实实地提高学生的程序设计能力。

而在众多需要掌握的编程技巧中，“递归”不但是学生必须掌握的基本知识点，更是一种抽象和分析问题的模式。本文试着从教学实践的角度来谈谈如何辅助学生更快更好地理解“递归”编程方法（基于C/C++语言）。

一、函数调用的基本过程

其实，“递归”从程序运行的角度来说就是函数调用，因此准确理解普通函数之间的调用过程有助于理解函数“递归”调用的本质。

在设计程序解决问题时，为了减少编程难度和问题规模的可控，需要把大的问题和模块分解成若干子问题或者子模块，而这些子问题、子模块的求解往往是通过函数这个载体来实现的，这就必然会涉及函数之间的调用。清晰、准确地理解函数调用过程至关重要，但对于没有编程基础的中学生来说，这是一个比较困难的事情。更可行的办法莫过于从现实生活的应用实例出发，以可视化的方式来描绘、讲解函数调用过程[1]。

例如，在处理一篇学习资料时，中途遇到不理解的内容需要求助于其他方面的资料，就可以暂停原来的任务，转而去执行求助任务，等求助过程结束后再返回到原来任务的中断处，原任务重新启动并继续处理下去。这个过程大致分为以下几个阶段：（1）中断原来任务时，要在相应的地方做一个“标识”，目的是方便以后的任务重启。（2）在求助其他资料之前，往往需要提炼资料中的相关内容。简单地说，就是要做好带着“问题”去求助的准备。（3）求助任务开始执行，生成结果并返回。（4）回到原来的“标识”处，原先暂时中断的任务重新启动并继续执行下去。

函数的调用过程和上面的例子比较相似，例如，在主函数main( )中需要调用函数f( )，执行过程大致如下：（1）主调函数，也就是main( )函数，在调用f( )前也要做好“标识”工作，即保存当前现场，保存返回地址。（2）调用f( )函数，控制权交给f( )。（3）f( )执行并返回。（4）恢复主调函数的调用现场，恢复返回地址。至此，调用f( )的工作完成，主调函数根据恢复地址继续执行下去。调用过程如图1所示。

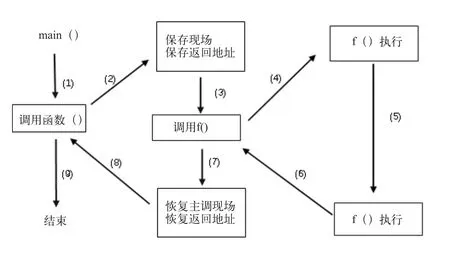
图1 调用过程

二、函数的递归调用

函数的递归调用就是直接或间接调用自己的过程。其本质和普通函数之间的调用并无二致，但是因为其特有的自己调用自己的特性，往往会使得学生在理解上产生困惑和混淆。例如，有的学生会把递归误解成循环或者函数复制。教学实践中发现，如果教学案例选择设计得当，并配合准确的表述和可视化的图解，那么帮助学生准确理解递归执行过程的目的是完全可以达到的[2]。

试举一例，要求整数n的阶乘。已知：

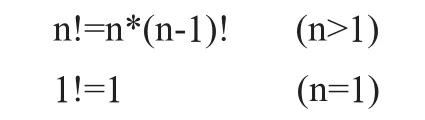
现在定义函数f(n)来求解n！。参考代码如下：

main( )函数中调用f(n)时，把3赋值给了参数n，之后f(n)进行了若干次递归调用，递归到边界之后便停止此过程，然后开启了返回结果的过程。现在把该代码的执行过程简单图解，如图2所示。

最终f(n)函数返回主调函数main( )时，返回值是6，并赋值给s。

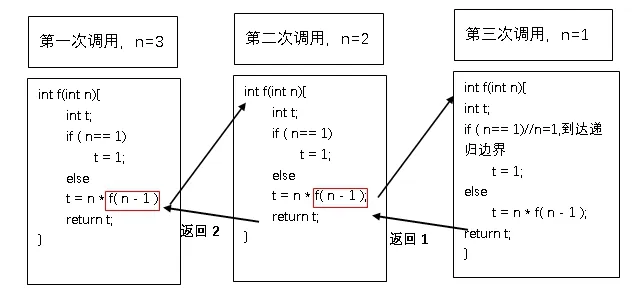
图2 代码执行过程图解

总结图2可知：（1）递归调用首先会发生一系列不断自我调用的过程，也就是不断向边界逼近的过程。（2）递归一定要有边界，也就是递归到某个状态时就会得到结果，此后递归调用不再继续。（3）递归一旦停止就会开始恢复上一层中主调函数的调用现场，从而实现逆序回归的过程。从上面的分析可以看出，递归绝对不是循环，每一次递归调用并不是把原来的函数代码复制一份。递归的过程中，计算机系统不断进行着把调用现场、变量、返回地址等有序保管到堆栈、内存空间中的工作，等递归结束之后又通过出栈的方式把主调现场恢复，然后逐步返回。

三、递归思想应用一般方法

使用递归思想来设计算法是有其特殊的优点的。例如，会使程序简洁明了、易读易写、结构简单等。但是递归方法不能包打一切，是有适用的场合的。以上例中求n！为例，求f(n)的问题可以转成求f(n-1)的问题，而且可以不断地转变下去。这样的转变之所以能成立，是因为转变前后问题的本质是一样的，算法思想是一致的，只是求解的数据规模不同而已。转变的过程就是把问题的规模不断缩小的过程，当然转变不能无限制地进行下去，它肯定会遇到一个临界点，在这个临界点程序会生成一个初始结果，然后系统会掉转方向，回溯过去，最后得解。也就是说，能使用递归的方法解决的问题必须要符合下面的条件：（1）能够设计出表达式把原问题转变成子问题。（2）子问题的规模比原问题要小。（3）子问题可以通过表达式转变成子问题或者因为递推到边界而直接得解。（4）通过整合子问题的解，能够回溯推出原问题的解。

试举一例，求整数m，n（m＞n）的最大公约数。小学数学中就有此类问题的解法，简单来说，就是把两数的公有质因数求解出来并相乘，便可得出最大公约数。但这个算法不适用递归思想，一方面，它很难做到规模更小；另一方面，它很难用同样的表达式求解子问题。

此外，著名的欧几里得定理也能解决求最大公约数（gcd）的问题。它的公式是这样的：

gcd(m,n)=gcd(n,r)，r=m%n，（m＞n,m,n,r都是整数），当r=0时，n的值就是解。

分析：（1）原问题的m、n的规模较大，而子问题n、r的规模明显变小。（2）原问题和子问题的求解表达式是一致的。（3）存在递归边界，即r=0时便可以求得解。可以看出该定理的本身就是递归的，因此，使用递归的方法来设计并编写程序就是顺理成章的了。参考代码如下：

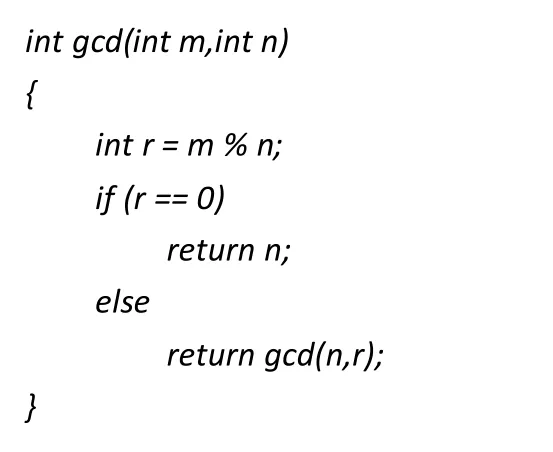
综合前面几个例子，可以非常明显地看出使用递归思想设计出来的程序简洁优美。但是矛盾是无处不在的，递归在保证优美的同时付出的代价是系统开销增大，执行速度变慢，因此即便是能使用递归的场合也要谨慎使用。

结 语

本文站在实际教学的角度，分析了学生在学习和使用递归方法上存在的困难，并给出了解决办法。递归是一个非常好的编程方法，也是一种很棒的解决问题的模式。教育教学方法的探索和创新是无止境的，如何准确把握学生在信息学习上遇到的困难和思维盲点并给出有效的解决方案，是值得每一个教师认真研究的。同时，我们要把这些研究、探索和新一轮的信息技术课程改革中提出的培养学生的计算思维的目标有效结合起来，始终紧扣时代主题，从学生终身发展的战略高度出发，努力提高学生的程序设计水平和解决问题的能力。