浅谈初中数学教学中如何培养学生的数学思维
2018-09-13张程
张 程
(江苏省南通市小海中学,江苏南通 226015)
引 言
数学是一门较为严谨、逻辑性较强的学科,在初中数学教学中,教师如果只是要求学生记住几个公式,这很难帮助学生形成良好的数学思维。而当学生进入高中,面临更大难度的数学知识时,就会表现得束手无策。为了避免这种问题的出现,教师必须重视对学生数学思维的培养,让学生学会用数学的观点来看待和解决问题,真正促进学生的长远发展。
一、通过课堂导入激活学生的思维
数学思维的形成是一个周期性的过程,仅仅依靠几次课堂教学是不可能达到理想效果的,而是需要教师引导学生掌握线索,逐步深入、层层递进。为此,教师可以利用课堂导入来激活学生的思维,避免理论教学带来的突兀感。例如,在二次函数应用题的教学中,主要引导学生结合二次函数知识了解自变量与因变量的关系,从而建立函数表达式,解答实际问题[1]。
为了更好地激活学生思维,教师结合实际生活情境,引导学生进行讨论。教师结合生活中的热点事例,如售价与利润之间的关系,引导学生讨论问题:某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,商场决定采取降价措施。调查发现,每件衬衫每降价1元,商场每天可多售出2件,设降价为x元,求平均每天利润Q的表达式。教师引导学生思考这道题,要想算出利润,学生首先要写出平均每天销售量的表达式:y=20+2x。之后,学生就可以根据利润=每件盈利×销售量,求出利润。这样,学生通过生活化的情境,充分了解了售价与利润之间的函数关系。接着,教师则引入相关数据,创设良好的应用题情景,学生则能够结合数据列出表达式解答习题。让学生按照步骤逐步启发思维,提高了学习效果。通过这样的方式,设置有效的课堂导入,更好地激活了学生的思维,让学生为深入的课堂学习做好准备。
二、加强对教学方法的改革与创新
基于培养学生数学思维的目标,通过对以往的教学经验进行研究,教师发现传统的教学方法难以起到良好的效果。为此,教师应当尝试用创新的观点组织教学,弥补传统模式的漏洞,产生强劲的动力[2]。例如,在“平行线的公理与性质”的教学中,主要引导学生了解直线平行的性质,以及如何判定直线平行。这些知识涉及比较多的定理,而许多教师只是引导学生对定理进行记忆,学生并不知道这些定理由何而来,这对培养学生的数学思维十分不利。教师要优化教学设计,既要引导学生了解浅层的文字内容,也要引导学生理解深层的内涵。于是,教师首先在黑板上画出两条平行的直线,让学生通过量角器、直尺等工具找到图形中的数量关系。这时,学生会有一些简单的收获,并且提出一定的猜测,教师则可以借助这些猜测,引导学生进行进一步探究,用数学语言进行有效验证,从而帮助学生了解知识的推理过程,从思维角度形成有效理解。通过这样的过程,让学生深入了解公式定理的研究过程,强化学生的思维能力。
三、锻炼学生的学习与总结能力
在初中数学教学中培养学生的数学思维体现在方方面面,知识教学只是基础环节,更重要的是培养学生的学习与总结能力。为此,教师要加强教学设计,从各个方面锻炼学生的学习与总结能力[3]。例如,在“归类推理思想”的教学中,教师结合多边形内角和的案例向学生传授知识,但是忽略了过程研究,只是直接展示探究产生的公式。这样的教学过程注重灌输,学生缺乏实际锻炼。教师必须改变策略,引导学生进行探究性学习,深入分析探究过程,掌握分析的思路与方法,并加强对探究成果的理解,提高自身的学习能力。为了锻炼学生的总结能力,教师则可以转变习题教学模式,融入更多总结的成分。
四、开发与培养学生的创造性思维
培养学生的数学思维,并不只是让学生学会思考有限的数学问题,而是要让学生产生创造性的思维。例如,在“二次函数动点问题”的教学中,教师主要引导学生从函数知识的性质进行定性研究,将各种情况讨论出来。而基于培养学生创造性思维的目标,教师要引导学生另辟蹊径,抛开传统模式的限制。这时,学生积极展开思考,能够发现数形结合的思维方式在这类习题中有着突出的应用优势。然后,结合习题内容,充分展开想象,利用铅笔将动点的轨迹画出来。再结合相关数据进行分析,从而有效地解答习题,也将函数知识与实际图形有机结合起来,提高了学习效果。通过这样的方式,开发与培养了学生的创造性思维,打造具有数学智慧的学习过程。
五、突破学生以往的定势思维
由于初中数学教学模式长期受到应试教育理念的干扰,导致学生在学习数学时容易出现思维定势的问题。为了进一步培养学生的数学思维,则要消除学生这些思维定势。很多学生因为没有足够的经验或缺乏联系实际的意识,往往会依赖个人的臆断。因此,教师要注意引导学生打开思维的天窗。虽然思维定势有时能够帮助学生更好地掌握解决常规问题的方法,进一步实现知识的迁移,但有时也会严重干扰学生的思维,限制学生的视野拓展。所以,为了锻炼学生运用知识解决实际问题的能力,教师往往要求学生以实际的生活情境为背景进行探索,了解其中隐含的数学知识,进一步开拓思考路径。另外,让学生突破以往的思维定势,能够帮助学生更好地利用题目条件,找出隐藏的关键信息。教师布置了一个几何证明题:如图1所示,已知矩形ABCD,E、F是 AD边的三等分点,且AB=1/3AD,求证∠AEB+∠AFB+∠ADB=90°。 首先,学生看到这道题,会下意识地把角当作唯一切入点,想方设法地在这三个角之间找关系,恰恰忽略了AB边和AD边的关系。一旦利用好这一关系 ,就能使数量关系浮现出来,这对学生解答本道题会提供很大的帮助。
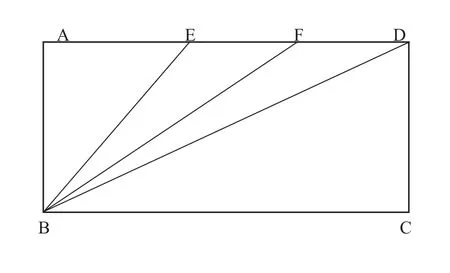
图1
结 语
总而言之,在初中数学教学中培养学生的数学思维是核心素养培养理念的基准要求,也是发展学生学习能力的价值体现。随着社会的发展和进步,人们对于数学教学的要求已经不仅仅局限于传授知识、掌握技能这些方面,而是更希望学生能够真正实现数学思维的拓展,建立良好的情感态度和价值观。
