基于金刚石氮-空位色心的精密磁测量∗
2018-09-11彭世杰1刘颖1马文超1石发展1杜江峰1
彭世杰1) 刘颖1) 马文超1) 石发展1)2)3)† 杜江峰1)2)3)‡
1)(中国科学技术大学,中国科学院微观磁共振重点实验室与近代物理系,合肥 230026)
2)(中国科学技术大学,微尺度物质科学国家实验室,合肥 230026)
3)(中国科学技术大学,量子信息与量子科技前沿协同创新中心,合肥 230026)
1 引 言
在特定的条件下,具有自旋的微观粒子可以从一定频率的交变磁场中吸收能量,即发生磁共振现象.基于这一现象发展起来的磁共振谱学和成像技术可以被用来准确、快速和无破坏性地获取物质的组成和结构信息,是当代最重要的科学技术手段之一[1,2].正因如此,磁共振谱学和成像领域的科学家六次获得诺贝尔奖,包括物理学、化学和生命科学.如今,磁共振波谱学和谱仪已被广泛用于分子结构的解析,而磁共振成像更是成为主要的医学诊断手段之一.
当前通用的磁共振波谱仪主要是核磁共振波谱仪和电子顺磁共振波谱仪,它们一般基于磁感应的原理,测试对象是含有大量相同自旋的系综样品.受限于探测原理,其分辨率通常在亚毫米级别,极限在微米量级,对应的分子数在数十亿以上.然而,近年来随着物质科学探索的不断深入,技术手段逐渐从宏观向微观迈进.在自旋磁共振领域,实现微观磁共振乃至单分子或单自旋磁共振,是这一方向极为重要的科学目标.
金刚石的氮-空位(NV)色心是金刚石中的一种点缺陷.自1997年实现单个NV色心的光探测磁共振以来[3],这一体系逐步受到了人们的广泛关注.室温下,NV色心这一固态单自旋体系具有毫秒量级的相干时间,可用光学共聚焦系统进行初始化和读出,并且利用交变磁场实现单个自旋量子态的调控.这些优良性质使之被用于量子计算、量子模拟以及量子物理基本问题的实验研究.近年来,以该体系作为磁信号量子探测器的微观磁共振技术快速发展,已经实现纳米分辨率、单自旋灵敏度的微观磁共振,在物理学、化学、生物学等领域具有广泛而重要的应用前景[4−7].
本文以微观磁共振研究为重点,介绍金刚石NV色心体系及其在精密测量领域的应用.主要包括以下几个内容:NV体系的性质和用于测磁的原理,微观磁共振的国内外研究进展和趋势以及总结和展望.
2 金刚石NV色心的性质和用于测磁的原理
2.1 NV色心的结构和光跃迁性质
纯净的金刚石是无色透明的,若含有适量的杂质则会显现出颜色,比如含有一定量硼的金刚石呈蓝色,掺入一定量氮的金刚石呈黄色.即使看起来无色透明的金刚石单晶也可能含有大量的杂质,其中有测试数据的顺磁性杂质缺陷就有近百种,而最常见的一种杂质就是氮,它以氮原子或氮原子簇的形式存在.按照含氮量的不同,金刚石可被分为以下四种:1)Ia型,含氮量高于0.3%,常见于天然形成的金刚石;2)Ib型,包含大于500 ppm的氮原子,人工合成的金刚石大多属于这一种;3)IIa型,非常少见,含氮量极低;4)IIb型,p型半导体.
如图1(a)所示,当金刚石晶格中有一个氮原子取代了碳原子,而相邻位置又缺少一个碳原子而留下空位时,就形成了氮-空位色心,即NV色心.大多数NV色心带有一个负电荷或处于电中性状态,分别记为NV−和NV0.本文中提到的NV色心均指NV−,它有六个价电子,占据四个分子轨道.基态和第一激发态的电子排布如图1(b)所示.
第一激发态与基态的能级差为1.945 eV,对应的波长是637 nm,实验中常用532 nm的激光来激发这一跃迁.处于激发态的NV色心有两条主要的退激发途径,其中之一是发射荧光回到基态,另一条途径是发生系间窜越(intersystem crossing),经由单态1A1和1E回到基态,这一过程不辐射荧光.这两条途径的发生概率依赖于NV色心电子的自旋状态,这是该电子自旋能够被光极化和读出的关键原因.经过连续的激光照射,电子自旋可以被极化到ms=0的状态;通过对收集到的荧光光子数进行分析,可以得知电子自旋处于ms=0的概率.在低温下,甚至可以利用共振激发来单次读出电子自旋的状态.

图1 NV色心的结构与光跃迁性质 (a)几何结构;(b)基态和第一激发态的电子排布;(c)能级结构和光跃迁性质Fig.1.Structures and optical transition properties of a negatively charged NV center:(a)Geometric structure;(b)electron configuration of the ground state and the first excited state;(c)energy level structure and optical transition properties.

图2 (a)金刚石表面的固态浸没透镜;(b)金刚石纳米柱Fig.2.(a)Solid immersion lens on the diamond surface;(b)nanopillars on the diamond surface.
金刚石的折射率高达2.42,大部分NV发射的荧光光子会由于界面的全反射而无法被探测到.实验中,为了提高荧光的收集效率,可以在表面刻蚀一些微结构.例如,可以用聚焦粒子束在金刚石上刻蚀固态浸没透镜,或者用化学反应刻蚀工艺制备金刚石纳米柱,如图2所示.
2.2 NV色心的基态哈密顿量
目前,大多数基于NV色心的实验是围绕其基态3A2实施的.以NV晶轴为坐标系的z方向,并适当地选取x和y方向,则NV色心基态电子自旋的哈密顿量可以写为

本文中将普朗克常量h设为1,哈密顿量都采取频率量纲.(1)式中,第一项描述纵向的零场劈裂,在常温常压且没有额外纵向应力的情况下,纵向的零场劈裂常量D约为2870 MHz;第二项描述横向的零场劈裂,在没有外电场和横向应力的情况下E=0;第三项描述电子自旋的塞曼劈裂,旋磁比是γe=−2.8 MHz/G.本文中,用Sx,Sy和Sz代表NV电子的自旋角动量算符,自旋数为1;S代表以Sx,Sy和Sz为分量的矢量[8].
氮的两种稳定同位素是14N和15N,二者的自旋数分别是1和1/2.考虑NV色心本身的氮核自旋之后,哈密顿量写为

式中的后两项分别是氮核与电子的耦合项以及氮核自身的哈密顿量,其表达式分别为

(3)式中Ix,Iy和Iz代表氮核的自旋角动量算符,I代表以Ix,Iy和Iz为分量的矢量;耦合常量a⊥和a||的绝对值的范围是2—3 MHz.对于14N,旋磁比γN= −0.3077 kHz/G,电四极劈裂常量Q= −4.95 MHz;对于15N,旋磁比γN=−0.4316 kHz/G,无电四极劈裂.
金刚石中通常还有大量13C.以天然丰度1.1%来估计,金刚石中半径为5 nm的球体内约有500个13C.如果计入与NV有较强耦合的13C等其他自旋,那么总的哈密顿量将在(2)式的基础上增加相应的项.
2.3 NV色心基态的操控与弛豫
通常情况下,可以利用微波或射频波段的交变磁场对NV色心的基态电子自旋、氮核自旋乃至邻近的其他自旋进行相干操控,并由此实现各种量子逻辑门.在金刚石NV色心体系上,保真度0.999952的单比特门和保真度0.992的双比特门已被实现[9].这些量子逻辑门的保真度达到了容错量子计算的要求.也可以施加交变磁场对NV周围耦合较强的其他自旋进行操控,实现更多比特的量子逻辑门[10].

图3 几个常用的动力学解耦脉冲序列 图中所示的πx/2脉冲使量子比特的态矢绕着x轴旋转π/2角度,πx脉冲使量子比特的态矢绕着x轴旋转π角度,πy脉冲使量子比特的态矢绕着y轴旋转π角度;首尾两个πx/2脉冲之间的部分为解耦序列Fig.3.Several common dynamical decoupling sequences.The πx/2 pulse rotates the state vector of the qubit around the x axis for an angle of πx/2.The πxand πypulses flip the state vector around the x and y axes,respectively.The decoupling sequence is between the two πx/2 pulses.
弛豫分为纵向弛豫和横向弛豫,前者是布居度回到玻尔兹曼分布的过程,后者是退相干的过程.一般情况下,NV色心基态电子自旋的纵向弛豫由声子主导,其速率与温度有关;在极低的温度下,声子的效应被抑制,纵向弛豫由自旋之间的相互作用主导,其速率与自旋浓度有关.对于顺磁杂质浓度较高的金刚石,当不同种类自旋的跃迁频率接近时,自旋间相互作用诱导的纵向弛豫会显著增强[11].纵向弛豫的特征时间通常记为T1.一般而言,NV色心基态电子自旋的横向弛豫由自旋之间的相互作用及静磁场的涨落造成.实验常用的超纯金刚石中顺磁杂质的含量极低,此时对NV色心电子自旋的相干造成影响的主要是13C核自旋.这种情况下,如果不对NV色心电子自旋施加任何保护,那么相干时间往往只有数百纳秒到2µs,这个相干时间通常记为对电子自旋施加动力学解耦脉冲序列,是延长相干时间的常用手段[12−14].常用的动力学解耦序列包含若干翻转脉冲,如图3所示.通过适时地翻转中心自旋,可以把一部分噪声平均掉.动力学解耦作用下的相干时间通常记为T2.
2.4 NV色心测磁的原理
近年来,NV色心引起了越来越多的关注,其优势大体上包括以下几点:1)较长的相干时间,这使得更多更久的相干操作得以进行,并且有更久的时间用来积累更多的信号;2)高灵敏度,NV色心单量子干涉仪测量磁场灵敏度可达10−9T量级[15],而NV色心系综甚至达到了10−13T量级[16];3)高空间分辨率,由于NV色心电子波函数的空间范围在几个晶格之内,故其磁场测量空间分辨率可达到亚纳米[16,17];4)易于初始化、操控和读出,室温大气环境下,NV色心的电子自旋可通过光跃迁进行量子态的初始化和读出,用微波或射频进行量子态的操控,与NV色心电子自旋有较强耦合的其他自旋也可用适当的方法进行初始化、操控和读出[18];5)丰富的能级结构,NV色心的电子基态具有三能级结构,再结合邻近的耦合自旋,提供了多种量子比特的编码选择.这些优势不仅使得NV色心被用于量子计算[10,19−21]、量子模拟[22−24]以及量子力学基本问题[25−27]的实验研究,更使其成为精密测量的利器[17,28].
不同种类的待测信号对NV色心哈密顿量的影响不尽相同.例如,温度的变化会显著影响纵向零场劈裂的大小[29−32],横向的应力或电场会造成横向的零场劈裂[33,34],外加的磁场会改变塞曼劈裂,附近的自旋会施加耦合作用.本文的重点是测磁,磁信号可能是由外界直接施加,也可能是来自其他自旋.随着待测磁信号种类和强度的不同,采取的测量方案也不尽相同.这里介绍三类方法.
一个常用的方法与干涉仪的原理类似,如图4所示.其主要过程是先将NV色心基态电子自旋制备到两个本征态的等幅叠加态上,然后让该体系在待测场中演化;其间两个本征态上积攒的相位是不同的,由此造成相对相位的差异;最后将这个相对相位转化为布居度读取出来,即可获取待测信号的信息.若待测信号是幅度较小、频率较低的交变磁场或耦合较弱的自旋,则可以利用动力学解耦序列来抑制噪声、累积信号,从而提升测量效果.运用这种方法,测得的信号在频域上的线宽由横向弛豫速率决定,约为1/T2的量级.为了减小线宽、提高谱线分辨率,可以采用关联谱方法,其脉冲序列如图5所示.运用这种方法,线宽可缩窄至1/T1的量级[35,36].
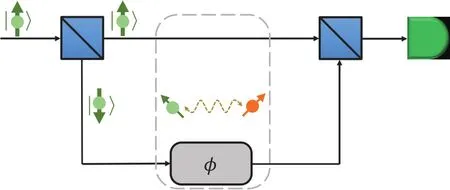
图4 NV色心干涉仪NV色心与被测自旋相互作用,在叠加态上产生相对相位,通过干涉将该相位信号转化为布居度信号进行读出Fig.4.NV center as an interferometer.The interaction between an NV center and a target spin results in a relative phase factor on the superposition state of the NV center.This phase factor is converted into the population and read out at last.

图5 关联谱脉冲序列 一轮实验中,时间间隔τ通常是固定的,而τ′是变动的,其他动力学解耦序列可以替换上述序列中Hahn回波的部分Fig.5.Pulse sequence for correlation spectroscopy.In one run of experiment,the time interval τ is usually fixed while τ′is variable.Other dynamical decoupling sequences can replace the segment of Hahn echo in this sequence.
如果待测的是随机涨落磁信号,那么可以通过监测NV色心基态电子自旋的弛豫过程来获取目标信号的部分信息[37].其大致做法是:先将NV色心制备到某个本征态上,然后监测其纵向弛豫;或者制备到两个本征态的等幅叠加态上,然后监测其横向弛豫过程.弛豫速率的大小反映了随机涨落信号的强弱,而这往往由待测自旋的浓度以及与NV的距离等因素决定.
待测信号会对NV色心基态哈密顿量产生影响,造成额外的能级劈裂.如果信号是不含时的,并且造成的能级劈裂大于线宽,那么一般能用扫谱的方式来测量.具体而言,可以对作为探测器的自旋施加交变磁场并扫描频率,当频率与能级差匹配时,便反映为谱上的峰或谷.也可以采用自旋锁定方法,如图6所示.该方法中,当驱动场的幅度与待测自旋的能级差匹配时,在谱上也可以显现峰或谷[38].

图6 自旋锁定脉冲序列序列开头和结尾的脉冲的作用分别是绕着y轴和−y轴的π/2旋转;中间施加绕着x轴的连续驱动,其幅度可变Fig.6.Pulse sequence for spin-locking.The initial and final pulses implement π/2 rotation around the y and−y axes,respectively.In between is the continuous driving with variable amplitude around the x axis.
3 微观磁共振的国内外研究进展和趋势
作为高灵敏度、高空间分辨率的明星量子传感器,NV色心有着独特的优势,如图7所示.这使得NV色心在物理、生物、材料等领域有广泛应用前景.例如,在物理和材料科学领域,人们实现了纳米尺度质子自旋的磁共振探测[40,41],且进一步达到了单质子灵敏度[42];实现了对纳米线磁畴畴壁的成像和操控[43];实现了对金属中的Johnson噪声的探测[44].在生物学领域的应用尤为突出,实现了细胞内的灵敏的温度探测[45]以及对细胞的成像[46],完成了对趋磁细菌的磁场探测和成像[47],完成了对单个蛋白质分子的磁共振探测[48].
3.1 纳米尺度的核磁共振
长期以来,纳米尺度的样品乃至单分子、单自旋的核磁共振一直是个难题.为了解决这一难题,首要的任务便是探测纳米尺度的核自旋样品乃至单个核自旋,而NV色心在这方面有着突出的表现.如果核自旋与NV色心电子自旋的超精细耦合足够强,即耦合强度大于电子自旋的磁共振谱线宽度,那么该核自旋会使电子自旋的谱线发生劈裂,由此反映出关于耦合的部分信息[49−51].对于耦合较弱、不能在谱线上直接分辨的核自旋,往往可以通过施加动力学解耦进行分辨.上文已经提到,动力学解耦可以抑制噪声、延长相干时间;与此同时,动力学解耦也可以积累特定频率的信号,使微弱的信号被探测到,这相当于锁相探测(lock-in detection).例如,对单个NV色心的电子自旋施加最简单的动力学解耦序列,即Hahn回波或CPMG-1,便有可能探测到NV色心周围的13C核自旋库[52].通过施加高阶动力学解耦脉冲序列,还有可能探测到若干弱耦合的单个13C核自旋[53−56].

图7 各种测磁体系的指标对比[39]Fig.7.Capabilities of magnetometers based on various physical systems[39].
2013年,德国Stuttgart大学的Wrachtrup研究组与中国科学技术大学的杜江峰研究组合作报道了在室温大气环境下成功检测到约(5 nm)3体积的有机物样品的质子自旋信号[40].该实验使用的NV色心在金刚石表面以下约7 nm,通过对其电子自旋施加高阶动力学解耦,探测到约104个质子自旋.同时,美国IBM研究部的Rugar研究组[41]也报道了对(24 nm)3有机物样品中质子自旋的检测,所选用的NV色心在金刚石表面以下约20 nm;对其电子自旋施加低阶动力学解耦,而在电子自旋的自由演化期用射频对质子自旋进行操控,最终探测到约106个质子自旋.
2014年,德国Ulm大学的Jelezko研究组[42]报道了室温大气条件下对金刚石外四个29Si核自旋的单核自旋灵敏度的探测.该研究同样运用了动力学解耦方法,并且借助NV色心形成的梯度磁场,使单个原子核的定位精度提升到Å量级.
探测金刚石外的核自旋一般要用靠近表面的NV色心,而表面常有较多的电子自旋杂质;这些自旋通常会对探测造成干扰,但也有可能用来放大待测信号.2014年,美国Harvard大学的Lukin研究组[57]报道了利用表面电子自旋来放大质子自旋的信号.
以上几个例子中,测得的信号来自单个核自旋,或者由彼此几乎独立的若干单核自旋共同贡献,而核自旋之间的耦合在这些研究工作中并非关注对象.核自旋之间的相互作用携带着关于分子结构的丰富信息,对于分析化学十分重要,在量子计算上也有着潜在的应用[58].2014年,杜江峰研究组[59]报道了对核自旋之间耦合的观测.实验中,对NV色心电子自旋施加高阶动力学解耦,在室温大气环境下成功探测到距离NV约1 nm处的一对13C核自旋,如图8所示.研究者由实验数据分析出两核的耦合强度为690 Hz,并分析出两核的相对空间取向.这一研究工作实现了对亚纳米尺度的自旋簇的结构解析.
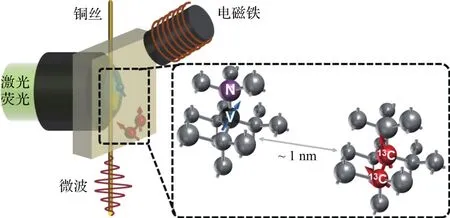
图8 单核自旋簇相互作用探测的实验装置示意图[59]Fig.8.Experimental sketch for sensing a nuclear spin cluster using the NV center[59].
利用NV色心进行核磁共振探测时,退相干效应使谱线增宽,从而影响一些重要信息的获取.相对于动力学解耦方法,关联谱能够提供更窄的线宽,从而取得更高的谱线分辨率.2015年,Jelezko研究组与杜江峰研究组合作报道了利用关联谱方法探测纳米尺度样品中的质子自旋,并测量到了油分子的扩散速率[60],该实验的装置如图9所示.2016年,瑞士ETH Zurich的Degen研究组[61]也报道了谱学方法类似的研究,并且展现了二维核磁共振谱.同年,Lukin研究组[62]报道了单个蛋白质分子中多个核自旋的磁共振.实验中,利用NV色心电子自旋和其自身的氮核自旋构成的双量子比特体系,测得了单个蛋白质分子中约两千个核自旋的磁共振谱.2017年,Wrachtrup研究组[63]也报道了谱线分辨率的提升.该实验将NV色心自身的氮核自旋用作量子存储器,并结合同核解耦脉冲序列,获得了纳米尺度样品中1H和19F核自旋的化学位移分辨率的磁共振谱.同年,Jelezko研究组和Degen研究组也分别报道了谱线分辨率的提升[64,65],Lukin研究组[66]报道了对二维材料的核四极共振.2018年,美国Harvard大学的Walsworth研究组[67]继续报道了谱线窄化.实验基于浅层的NV色心系综并结合了特殊的读出技术,获得了微米尺度10 pL体积的有机物样品的核磁共振谱,甚至分辨出标量耦合与化学位移.同年,杜江峰研究组[68]报道了纳米尺度冰晶中质子的核磁共振.实验中,通过测量大约7000个水分子的关联谱信号,解析了质子自旋之间的磁偶极耦合.

图9 纳米尺度冰晶中质子核磁共振的示意图[68]探测体积约为(6 nm)3Fig.9.Sketch of the proton nuclear magnetic resonance of nanoscale ice[68].The detection volume is about(6 nm)3.

图10 利用NV色心进行微观核磁共振的主要进展总结Fig.10.Major progress of the microscopic nuclear magnetic resonance based on NV centers.
近几年,NV色心也被用于微观核磁共振成像的研究[69,70].图10总结了利用NV色心进行微观核磁共振的主要进展.
3.2 纳米尺度的电子顺磁共振
电子顺磁共振是分子结构分析的重要方法.与原子核相比,电子的旋磁比高得多、弛豫更快,对快速动力学过程的探测也更加灵敏.纳米尺度乃至单分子、单自旋的电子顺磁共振同样可以基于NV色心来实现.2011年和2012年,两个研究组分别报道了基于NV色心的纳米尺度电子顺磁共振[71,72].实验中,浅层的NV色心电子自旋与修饰于金刚石表面的自由基电子自旋之间有耦合,利用电子-电子双共振技术可观测到自由基的电子顺磁共振.2013年,杜江峰研究组与Wrachtrup研究组合作报道了金刚石内单个电子自旋的探测[73];接着,Wrachtrup研究组报道了通过NV色心电子自旋的纵向弛豫过程来探测溶液中大量的顺磁离子[74].同年,有研究者报道了利用NV色心电子自旋的纵向弛豫来探测纳米金刚石表面的众多电子自旋[75].
2015年,杜江峰研究组[76]报道了单个蛋白质分子的电子顺磁共振谱.实验中,利用电子-电子双共振技术,对氮氧自由基标记的蛋白质分子进行了磁共振研究,如图11所示.该实验解析了自旋标记的部分结构,并提取了部分动力学信息.动力学信息的获取得益于氮氧自由基相对于外磁场的取向会对共振峰的位置产生影响,并体现在电子顺磁共振谱上.

图11 单分子顺磁共振的实验体系与方法[76] (a)实验装置示意图;(b)冻干的蛋白质在金刚石表面的分布;(c)脉冲序列Fig.11.Experimental system and method for single-molecular electron paramagnetic resonance[76]:(a)Sketch of the experimental setup;(b)distribution of freeze-dried proteins on the diamond surface;(c)pulse sequence.
然而也是由于取向对共振峰位置的影响,谱线会发生严重的非均匀展宽,这有可能导致重要信息被湮没.解决这一问题的典型思路有两条:一是通过施加强磁场来抑制谱线展宽的影响;二是完全不加磁场,从源头上移除非均匀展宽,此即零场顺磁共振.如图12所示,与非零场下谱峰位置依赖分子取向不同,零场下谱线位置始终不变,这使得不同取向的分子的叠加信号保持清晰.2018年,杜江峰研究组[77]还报道了对金刚石内部NV色心周围约15 nm范围内的约4个电子自旋的零场检测,获得了清晰的零场顺磁共振谱,并从中直接提取了目标自旋的超精细耦合常量.
2018年,Walsworth研究组[78]报道了对金刚石内电子自旋簇的探测与操控,该自旋簇由一对耦合的电子自旋构成.此研究工作中,NV色心同样发挥着传感器的作用,并被用于电子自旋簇的极化.

图12 跃迁频率随分子取向的变化关系[77] (a),(b)分别为非零场和零场条件下的模拟结果,待测对象是含15N的氮氧自由基,其主轴与NV晶轴的夹角设为θ;15N核自旋和电子自旋的超精细耦合张量的主值设为Axx=Ayy=23.2 MHz和Azz=144.4 MHz;在非零场条件下,模拟设置的磁场大小是300 G,方向与NV晶轴平行,探测方法是电子-电子双共振(DEER);在零场条件下,探测方法即为正文所述的扫描驱动场幅度Fig.12.Transition frequencies as functions of molecules’orientations[77]:(a),(b)Simulation results for a15N-labeled nitroxide radical under non-zero magnetic field and zero magnetic field,respectively. The angle between the principal axis of the nitroxide radical and the NV axis is denoted by θ.The principal values of the hyper fine coupling tensor between the15N nuclear spin and the electron spin are set as Axx=Ayy=23.2 MHz and Azz=144.4 MHz.In the case of non-zero field,the magnetic field is parallel to the NV axis with the magnitude of 300 G,and the detection scheme is double electron-electron resonance(DEER).In the case of zero field,the detection scheme is sweeping the driving frequency as mentioned above.
3.3 对微波与射频的测量
对微波和射频进行测量是NV色心的另一个应用领域[79−81].2015年,杜江峰研究组[82]报道了室温大气下纳米级分辨率的微波场测量,如图13所示.在共振的微波场的驱动下,电子自旋可发生Rabi振荡,振荡频率与微波场的强度和方向有关.实验中,通过测量拉比振荡的频率,并结合金刚石的单晶特性,完成了对2.6 GHz线偏振微波场的测量和矢量重构,矢量的角度和幅度精度分别为5.6 mrad和10−6T,空间分辨率达到了光学衍射极限(约230 nm).
对微波或射频进行高分辨率、高灵敏度的测量,不仅在工程技术领域有着重要价值,也为基本物理问题的研究提供了有力手段.2018年,杜江峰研究组[83]报道了对于一种新型相互作用的测量结果,该相互作用是由轴子或类轴子传递的电子与核子间的单极-偶极相互作用.实验装置如图14所示,一个SiO2半球在NV色心的上方做往复运动,其频率为187.29 kHz.如果电子与核子之间存在单极-偶极相互作用,那么这样的往复运动会对NV色心施加一个等效的交变磁场.该实验没有测得该交变磁场,这为单极偶极相互作用的耦合常数、力程以及轴子或类轴子的质量提供了新的界限.

图13 微波场测量的示意图[82] 波长为532 nm的绿色激光聚焦于金刚石表面以下数微米处,线偏振的微波场从一根22µm直径的铜丝辐射出来Fig.13.Schematic view of the setup for the microwave magnetometry[82].The 532-nm green laser is focused several micrometres below the diamond surface.The microwave field is radiated from a copper wire of 22µm diameter.

图14 电子与核子间单极-偶极相互作用的测量装置示意图[83] 核子由SiO2半球提供,半球附在原子力显微镜的音叉上,由音叉带动在NV色心上方振动,外加静磁场与NV晶轴平行Fig.14.Schematic experimental setup for the measurement of the monopole-dipole interaction between electrons and nucleons[83].The nucleons are provided by a fused silica hemisphere lens.The half-ball lens is placed on a tuning fork actuator of an atomic force microscope.A static magnetic field is applied along the symmetry axis of the NV center.
3.4 测量精度的继续提高
继续提高测量精度,对于进一步发挥该体系的优势十分重要.前面提到,利用NV色心单自旋体系进行精密测量时,往往将信号转化为相位信息加以测量,对相位的测量越准确,也意味着对信号的测量越准确.下面以相位的测量为例来介绍如何利用纠缠态来提高测量精度[84,85].
在核磁共振[87,88]、离子阱[89−92]、光学[93−95]、冷原子[96,97]等体系上,人们已经实验演示了对于标准量子极限的突破.在多粒子的非线性耦合体系上,超过1/N精度的测量也已被实现[98],但有人认为在该情形下海森伯极限需要重新定义,不再是1/N,真正的海森伯极限并未被突破[99−102].由于实验条件不完美,实际情况中海森伯极限一般无法达到,但突破标准量子极限是可以达到的.

图15 两种量子精密测量测量方案的示意图 (a)基于可分态的常规手段,其中每个量子体系彼此独立地参与初态制备、相位积累和读出过程;(b)基于量子纠缠的手段——相位积累之前的非定域操作用来制备纠缠,而相位积累之后也施加非定域操作,以便在纠缠基下进行测量Fig.15.Two protocols for quantum precision measurement:(a)Conventional means based on separable states where each quantum system undergoes the process separately and independently;(b)means based on quantum entanglement where the nonlocal operation before phase accumulation prepares an entangled state while the nonlocal operation after phase accumulation enables the measurement in an entangled basis.
在NV色心单自旋体系中,可以利用多个自旋的纠缠态来实现对标准量子极限的突破.例如,可以利用NV周围多个13C核自旋之间的纠缠、多个顺磁杂质原子的电子自旋之间的纠缠乃至多个NV色心电子自旋之间的纠缠.近年来,已对这一方法进行了初步的实验演示[103].该实验基于电子自旋和氮核自旋的耦合体系,利用两个自旋之间的量子纠缠,演示了相位测量中测量精度的显著提升.此外,运用巧妙的相位估计算法,也可以提升相位测量的精度[104,105].
4 总结与展望
金刚石NV色心是近年来备受关注的固态自旋体系,可用于磁场、电场、应力、温度等物理量的测量,其中测磁方面的进展尤为突出.例如,自旋之间存在着磁相互作用,可以利用NV色心对其进行探测,从而实现纳米尺度乃至单分子、单自旋的核磁共振和电子顺磁共振;也可以利用NV色心对外加的静磁场、交变磁场、随机磁场进行高灵敏度、高分辨率的测量.
金刚石NV色心在量子精密测量领域展现了巨大的潜力.随着微纳加工技术的继续发展、光探测磁共振实验技术的进一步提升以及各种方法和技术的不断涌现,NV色心将在量子精密测量中发挥进一步的作用.磁共振研究的新纪元正在开启,前景令人期待.
