时变参数模型的最优滚动窗宽选择标准及应用

傅 强，张兴敏

(重庆大学经济与工商管理学院，重庆 400030)

1 引言

结构不稳定性是研究领域中不可忽视的问题，静态模型难以捕捉样本关系的结构性变化[1-2]，对结构不稳定性的实证研究在金融风险测度、预警[3-8]，格兰杰因果关系检验[2,9]、宏观经济预测[10-12]等领域已有较大发展。为捕捉结构关系中的不稳定性，使用时变参数模型刻画经济序列间关系的方法被广泛使用，而参数的时变性常通过使用最近的观测值估计模型，也即滚动样本估计法实现。使用滚动样本技术的原因有：第一，该方法认为各变量间的关系随时间而变化；第二，经济序列中存在可能的结构突变，而滚动样本法能够捕捉到这种变化过程。

滚动样本技术是指在整个样本期内使用固定长度的滚动样本序列估计模型，得到一系列随时间变化的参数估计量，进一步地，可根据不同时点的估计模型进行样本外预测。选择多大规模的窗口宽度进行估计，是实践过程中需要解决的关键问题。

尽管关于滚动窗宽的选择问题类似非参估计中的带宽(bandwidth)选择问题，但对于使用滚动样本技术捕捉时变参数或进行样本外预测的窗宽选择问题却受到较少关注，且在应用过程中由于研究对象和目标有所差异。预测模型中，滚动样本技术的目标是使预测精度更高，而较少关注模型估计量的准确性，以及模型参数的时变性。时变参数模型中，滚动样本技术是为了捕捉参数随时间的变化趋势，更关注模型估计量的精确度及参数在不同子样本序列中的变化情况。当样本序列中出现一个或多个离散断点时，Pesaran和Timmermann[13]以提高预测精度为目的，提出了五种方法选择滚动窗宽。他们的方法中需要首先运用断点检验法(如，chow检验，累积求和统计量检验法(CUSUM and CUSUM-of-squares test)等)识别出未知断点的位置，并对断点前后的样本量进行取舍，进而估计出预测模型。当样本序列中出现多个连续和离散断点时，Pesaran等[14]推导了最优权重法确定预测模型所用样本量；Giraitis等[15]则基于交叉验证思想选择平滑参数,以减少早期信息的权重，进而得到更精确的预测量。而当断点信息未知时，Inoue等[16]提出以最小化近似预测均方误差选择最优滚动窗宽的方法。这些方法仅从预测视角出发，以预测精度为研究目的，且多以线性回归模型为研究对象。对于以捕捉参数时变性为目的的模型，它们选择的滚动窗宽无法达到提高模型估计量的准确性，捕捉参数结构突变性的目标。因此，预测模型下的最优窗宽选择标准对于时变参数模型可能并不适用。

时变参数模型对滚动样本技术的应用仍处于发展阶段，滚动窗宽的选择问题少有文献探讨。现有文献中，实验者或随意选择，或基于经验，或以年、季、月等时间截点选择滚动窗宽[4,6-7,17-19]，并没有形成统一明确的准则。实证表明模型的估计结果对于窗宽是敏感的，Nyakabawo等[2]认为滚动窗宽选择需权衡“模型估计的准确性和模型在各子样本期间的代表性”两个目标。基于此思想，他们选择了多个滚动窗宽，比较分析不同窗宽下变量的显著性水平，发现结果有显著差异，但没有建立最优窗宽的统计准则。Pesaran和Timmermann[20]证明了，当子样本的规模较小时，在子样本内包含多个模型的风险会随之减小。但较小的子样本规模却意味着参数估计的准确性随着标准误增加而下降。Khediri和Charfeddine[17]使用滚动样本法分析了现货和期货能源市场有效性的时变性，他们认为通过结构断点检验方法识别极端事件日期的做法并不合适，且多有文献进行批评。与此相反，Charfeddine和Benlagha[19]运用滚动样本法分析了copula模型中相依参数的时变行为，并使用结构断点检验法识别出极端政治、金融事件。他们认为，当数据集中出现一些断点时，短的滚动窗宽相比长的滚动窗宽能更好地捕捉参数时变性。Anagnostidis等[21]也认为滚动窗宽的选择对于模型的估计结果会产生较大影响，但他们没有建立相应的选择标准，而是选择多个时间窗口对比分析股票市场效率随时间的变化情况。可见，对于滚动样本的研究逐渐受到重视，但关于如何选择滚动窗宽仍缺乏深入的研究。

与现有研究的不同之处在于：第一，滚动样本技术是当前文献中常用的动态方法，但罕见文献探讨滚动窗宽的选择准则，本文以捕捉参数结构突变性为目的，建立了选择滚动窗宽的统计准则，弥补了当前该领域的空白。第二，在模型设定上，并不假定某一具体模型形式。将数据生成过程设置为单指标半参数模型，既可捕捉变量间的线性关系，也可捕捉非线性关系，假设条件较弱，适用性强。同时，当指标函数(链接函数)已知时，可拓展至通常情况下的线性回归模型和广义线性回归模型，此时只需使用对应模型的估计方法即可。因此，本文方法在应用范畴上较为广泛。第三，通过最小化估计量的近似二次损失函数及最大化各子样本估计量间的曼哈顿距离选择窗宽大小，同时考虑了模型估计量的准确性和时变性两个相悖目标。与传统上，仅根据主观意愿以时间截点选择滚动窗宽，以及与以预测精度为目标选择的滚动窗宽相比，在模型估计效果上有显著改善。第四，蒙特卡罗模拟实验和参数敏感性分析表明，本文方法能够捕捉到参数的结构突变性，且能满足参数估计量的准确性目标，证明了本文方法的有效性和稳健性。第五，将滚动窗宽选择标准运用到我国金融系统网络结构的构建中，捕捉金融网络的结构突变性，优化了动态网络模型。

2 研究设计

2.1 模型设定

假设数据生成过程(DGP)如下：

(1)

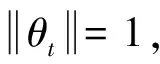
下文仅以单指标半参数模型为例，介绍局部线性迭代估计过程[22-24]。注意，以下参数中没有时间符号，原因在于这里的模型固定在一个时间窗口内，动态性由滚动样本技术捕捉，单个时间窗口的样本量为T1。首先对单指标半参数模型有以下假设：f(·)存在连续的二阶微分，对u=θTXt的某邻域内的ν，利用局部线性函数f(ν)可近似表示为f(ν)≈f(u)+f′(u)(ν-u)≡a+b(ν-u)，其中a=f(u)，b=f′(u)。并记Kh(·)=K(·/h)h-1，K(·)是核函数，满足条件：非负、有界、关于0对称且紧支撑以及Lipschitz连续，h>0为非参估计中的窗宽。则关于指标函数和指标参数的估计过程如下：

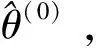
(2)

(3)

2.2 滚动窗宽选择标准

滚动样本技术中选择滚动窗宽时，需权衡两个相悖目标[2]：增加模型估计量的准确性，同时使各子样本期间模型的异构性最高。一方面，较小的子样本规模减少了子样本期内模型的异构性，提高了子样本内模型估计量的代表性，但增加了估计量的标准误差，从而降低估计量的精度。另一方面，较大的子样本规模提高了估计量的准确性，但降低了子样本期内所估计模型的代表性，特别是在存在结构突变的情况下。基于此，本文从理论上建立滚动窗宽的选择标准。以下为具体准则：

均方误差MSE表征了模型的估计优劣，可用于度量估计量的准确性；曼哈顿距离表征了变量之间的差异，可用于度量各子样本期间模型的异构性。在单指标半参数模型框架(式(1))下，指标函数和指标参数均未知，需要对其进行估计。因此，本文选择这两类估计量的均方误差之和作为模型估计优劣的判断标准。在线性回归框架或广义线性回归框架下，则只包含参数估计量的均方误差。设总样本量为T，滚动窗宽为l，每个子窗口的样本量为N=l+1，子窗口数目为T-l，在第m窗口下的两类估计量的均方误差定义如下：

指标函数f(·)的估计优劣采用均方根误差(RASE)表征，定义为：

RASE(m)=

(4)

指标参数θ的估计优劣采用参数均方根误差(PMSE)表征，定义为：

(5)

则最优窗宽准则定义为：

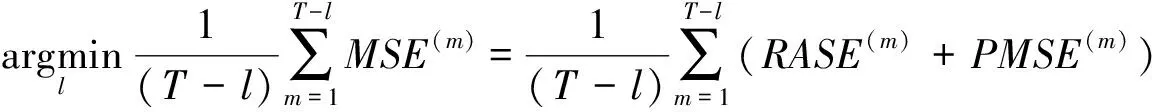
(6)

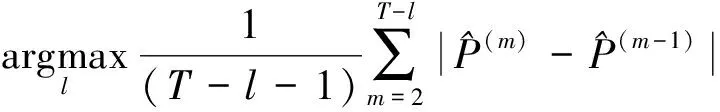
(7)

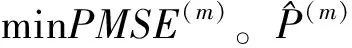
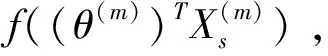
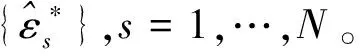
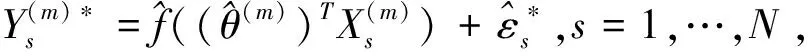
第五步：重复第二步至第四步K次，得到指标函数和参数估计量的Bootstrap值。

则均方根误差(RASE)的Bootstrap估计为：

(8)

参数均方误差(PMSE)的Bootstrap估计为：

(9)

则模型的Bootstrap均方误差(MSE)为：

(10)

本文中最优滚动窗宽的算法流程图见图1所示。本文算法的整体思路是，给定一个初始滚动窗宽值，采用局部线性迭代估计法估计模型，进而对样本使用Bootstrap法，得到模型的Bootstrap估计，求得近似均方误差值和曼哈顿距离值。对所有可行滚动窗宽执行相同的过程。最后再使用随机权重法，求得不同滚动窗宽下的评价函数，选择最小评价函数对应的滚动窗宽作为最终的最优滚动窗宽。

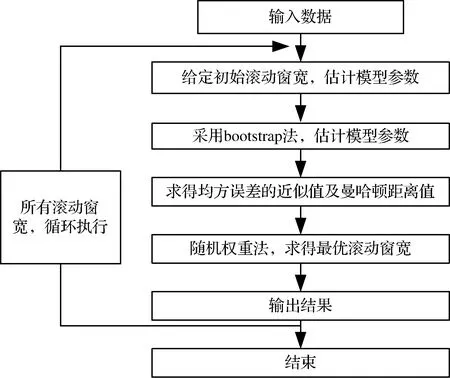
图1 整体算法流程图

根据上述算法可知，第一步的时间复杂度为O((T-l))(局部线性迭代估计，一般只关注收敛速率，不关注时间复杂度)，第二步的时间复杂度为O((T-l)*K)，第三步的时间复杂度为O(1)，所有可行滚动窗宽的循环步骤的时间复杂度为O(widths*(T-l)*K)，第四步的时间复杂度为O(widths*(T-l)*K*W)，则最终求出最优滚动窗宽的算法的时间复杂度为O(widths*(T-l)*K*W)。其中，widths为可行的滚动窗宽个数，(T-l)为选择滚动窗宽为l时的窗口个数，K为Bootstrap法中重复次数，W为随机权重个数。可以发现，时间复杂度O(nk)型，因此为有效算法。

3 蒙特卡罗模拟

本部分进行蒙特卡罗模拟实验，以检验前文中提出的最优滚动窗宽选择标准的表现。考虑了两种变量关系：线性关系(线性回归)和非线性关系(单指标半参数模型)，从均方误差MSE和曼哈顿距离分析本文方法(下文简称最优法)在捕捉参数准确性和时变性上的表现。由于现有文献对滚动窗宽的研究，均从预测角度并仅针对线性模型[13-16]。因此，在线性关系框架下(链接函数已知)，将最优法与预测均方误差法的结果进行对比。在非线性关系框架下(链接函数未知)，仅列出本文方法的估计结果。

预测均方误差法[13-16]通过最小化近似预测均方误差(MSFE)选择最优滚动窗宽。但与以预测精度为目的的方法有所区别的是，本文以估计时变参数为主要目的，故根据预测法[13-16]原理，结合前文中模型设定(1)式，具体准则如下：

(11)

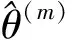
3.1 数据生成过程(DGP)

本文选择了两类数据生成过程，线性模型和非线性模型，以说明本文的方法对于线性关系和非线性关系均适用。数据生成过程如下：

yt=at*x1t+bt*x2t+εt

(12)

yt=exp(at*x1t+bt*x2t)2+εt

(13)

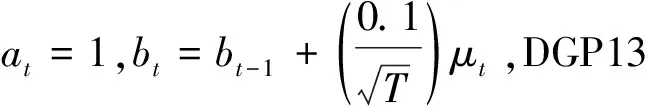
3.2 模拟结果

本文选择在样本量T=100和T=200时执行5000次蒙特卡罗模拟实验，评估线性模型和非线性模型的估计表现。表1和表2给出了模拟结果，包括各最优滚动窗宽对应的均方误差与全样本均方误差的相对比值、各子窗口间系数的曼哈顿距离。

均方误差相对值及曼哈顿距离值的具体计算公式如下：

(14)

(15)

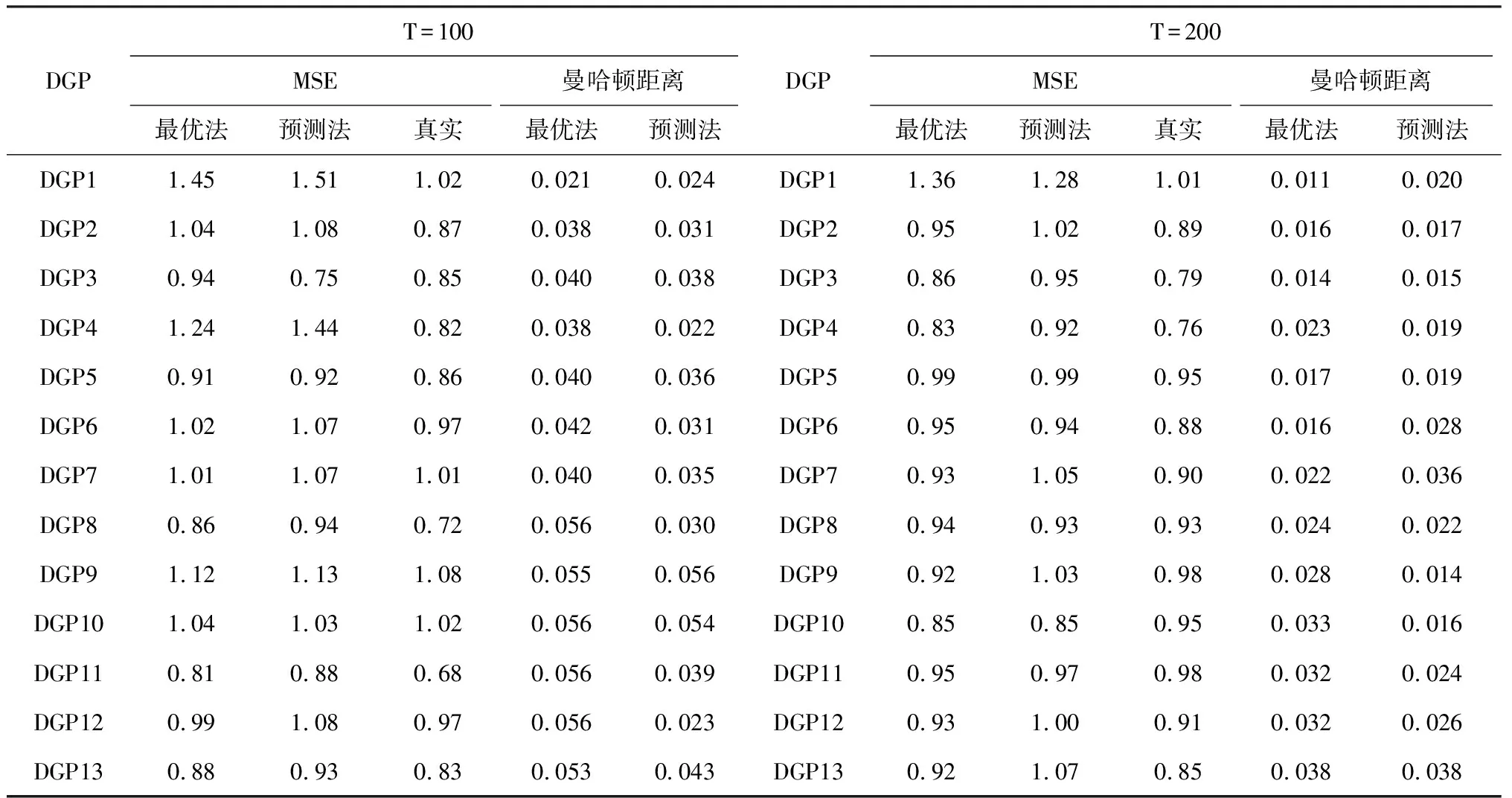
表1 线性模型的蒙特卡罗模拟实验结果

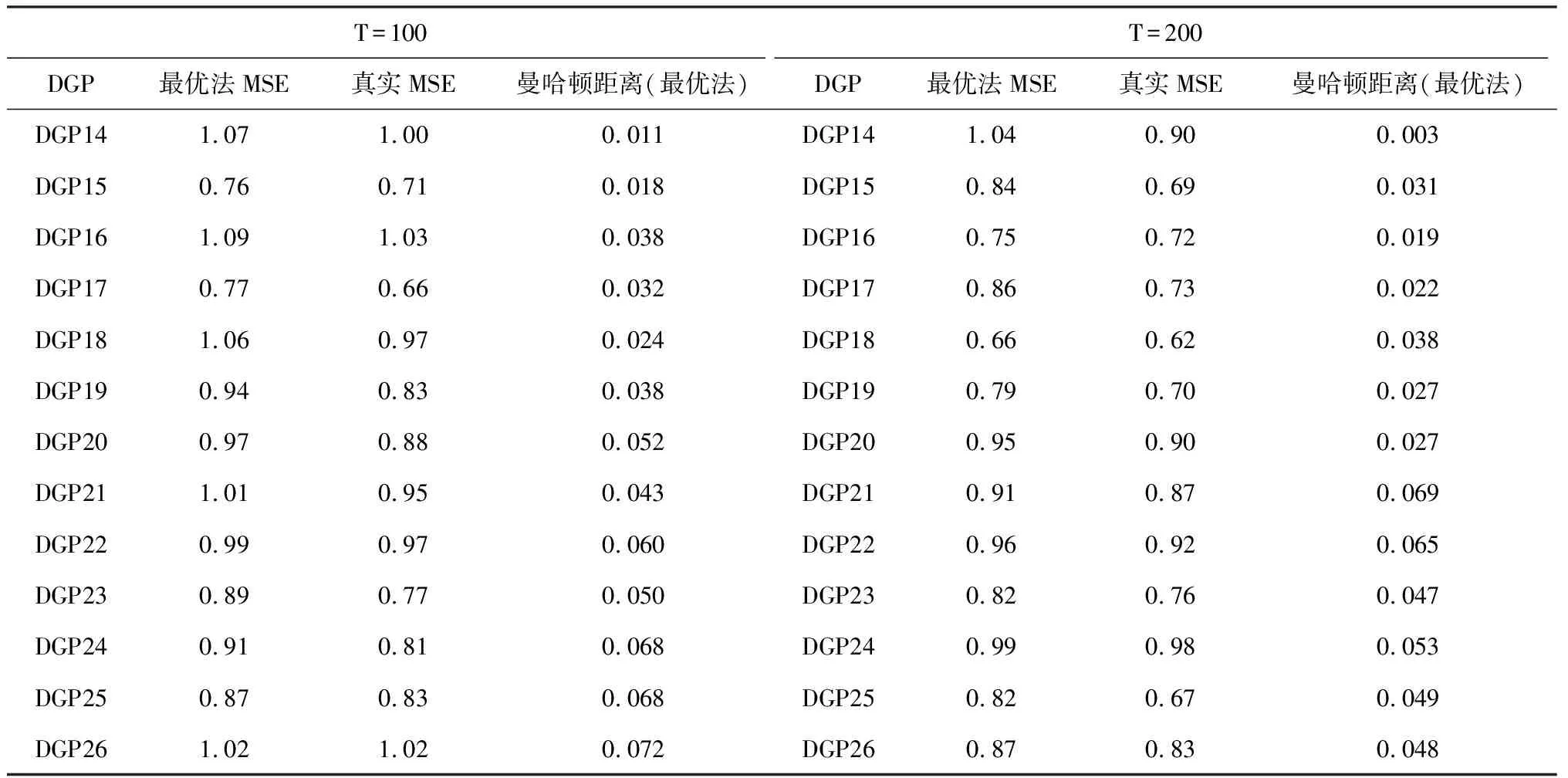
表2 非线性模型的蒙特卡罗模拟实验结果

根据理论分析可知，对于常参数模型，全样本估计的效果应该比滚动样本技术估计更优。在式(14)中，相对均方误差值小于1，说明滚动样本技术的估计表现优于全样本估计。根据表1和表2的结果，可以得到以下结论：

第一，真实均方误差(也是不可行均方误差)在所有数据生成过程中都得到了最小的相对均方误差值。在线性模型和非线性模型中，Bootstrap法得到的近似均方误差与真实均方误差比较接近。说明Bootstrap法能够用来估计线性模型和非线性模型的均方误差。

第二，当参数为常数时(DGP1，DGP14)，滚动样本技术相对全样本的均方误差比值较大。在线性模型框架下(DGP1)，最优法的估计表现优于预测法。总体而言，当参数不存在断点时，滚动样本技术的估计表现较差。因为假设样本中存在断点是错误的。但随着样本量增加，滚动法的表现存在改善。

第三，当参数出现离散断点时(DGP2-7，DGP15-20)，滚动样本技术的表现较常参数情况下好，且非线性模型较线性模型的表现好，但Bootstrap近似均方误差与真实均方误差仍有较大差异。在线性模型框架下(DGP2-7)，预测法的估计表现仍比最优法的估计表现差。

第四，当参数出现平滑连续断点时(DGP8-11，DGP21-24)，滚动样本技术的表现较好，且在线性模型和非线性模型下差别不大，最优法和预测法的估计表现差异较小，Bootstrap均方误差与真实均方误差比较接近，但仍较真实均方误差的表现差，因为Bootstrap法又增加了额外的误差。随着样本量增加，Bootstrap法的表现倾向于改善。

第五，当参数出现随机游走连续断点时(DGP12-13，DGP25-26)，Bootstrap法在线性模型和非线性模型框架下的表现较好，最优法和预测法的估计表现较好且差异较小。

第六，随着参数断点数目的增加，曼哈顿距离值呈增加趋势，说明该指标能够测度不同子窗口估计值之间的差异性。

以上分析表明，当参数出现连续断点时，本文提出的采用最小化Bootstrap近似均方误差，最大化曼哈顿距离确定滚动窗宽，得到的模型估计量表现较好。即使当参数不是连续断点时，Bootstrap近似均方误差的表现也是合理的，在缺乏更优准则情况时，也可以采用。在线性框架下，最优法的估计表现优于预测法，也说明了不能直接将以预测精度为目的的滚动窗宽选择标准用于以捕捉参数结构突变为目的的模型中。因此，通过求解最小化近似均方误差，最大化曼哈顿距离下的双目标优化问题，从而选择滚动窗宽的做法能够更好地捕捉参数的结构突变性，具有理论和实践意义。

3.3 参数敏感性分析

同一数据生成过程中，不同的参数设置可能会影响到最优滚动窗宽的选择和模型估计表现的稳健性，故对各数据生成过程中主要参数进行敏感性分析。分别分析线性模型和非线性模型在样本量T=100，几类典型数据生成过程：DGP1和DGP14(无断点)，DGP2-4和DGP15-17(一个离散断点)，DGP8和DGP21(平滑时变连续断点)，DGP10和DGP23(二次平滑时变连续断点)，DGP12和DGP25(随机游走连续断点)情形下，bt参数变化(变小或变大两种情况)对模拟结果(最优滚动窗宽对应的模型估计表现)的影响，分析结果见表3。

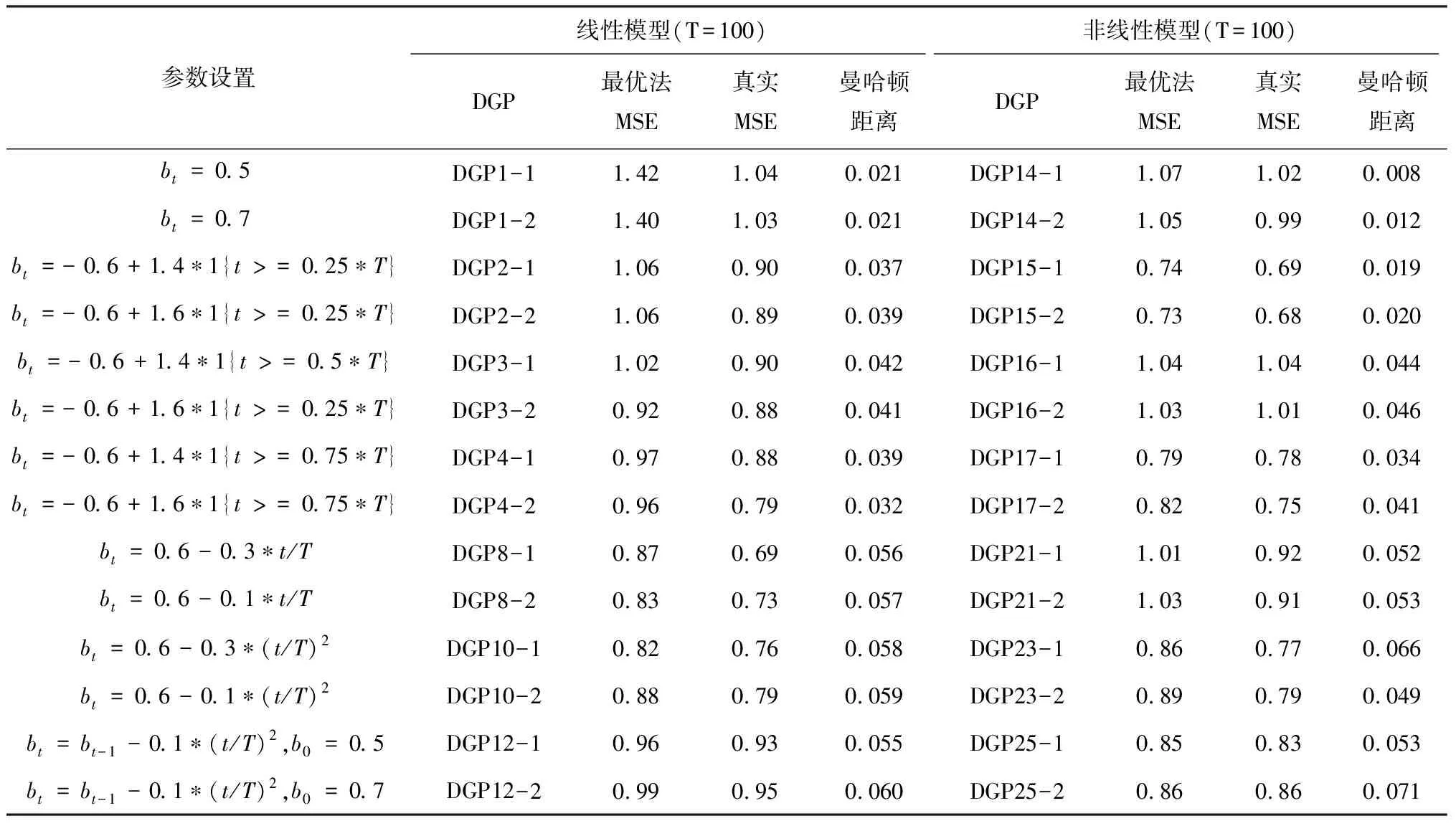
表3 主要参数敏感性分析结果

将表3与表1，表2对比可知，在各数据生成过程中，参数bt在某区间内变小或变大，对模拟结果(最优滚动窗宽对应的模型估计表现)影响较小，仍能得到与前文中仿真模拟相同的结论。在所有数据生成过程中，真实均方误差比值均是最小的，且Bootstrap近似均方误差值与真实值比较接近；随着断点数目的增加和连续性的增强，最优法表现更优。说明，本文的最优滚动窗宽选择标准对同类数据生成过程中参数变化不敏感，是稳健的。

4 实证检验

宏观经济系列通常受到外来冲击或社会经济制度改变的影响，从而处于长期不稳定状态，使用静态模型剖析金融经济序列结构显然不合理。Betz等[4], Härdle等[7], Paltalidis等[32]的研究已表明金融系统的网络结构呈现出了较强的结构突变性。本部分采用滚动样本技术研究我国金融系统的网络结构随时间的变化情况，以检验第二部分提出的最优滚动窗宽选择标准的实践价值。

4.1 模型简介

运用单指标分位数模型[7]构建金融网络结构:

(16)

(17)

(18)

(19)

表4 第m窗口下金融系统的网络结构

4.2 数据描述

选取2011年前已上市的30家金融机构，其中银行16家，保险公司3家和证券公司11家，样本周期为2010年10月16日至2015年9月26日，覆盖了2012年希腊债务危机，2013年银行业“钱荒”以及2015年股市崩盘事件。周频股票收盘价数据和财务数据来自于国泰君安数据库，宏观经济数据来自于Wind数据库。低频控制变量(季、月)采用三次样条插值技术转化为周频数据，高频控制变量采用均值法转化为周频数据。各控制变量定义[1,33-35]见表5。下文的实证过程在R软件中实现。

4.3 结果分析

金融系统的网络结构模型的估计表现及网络传染度由表6和图2给出。表6中给出了使用不同时间截点[4,7,36-37]选择窗宽、本文的最优法选择窗宽的模型估计表现，对比分析了不同方法的结果，以说明本文提出的滚动窗宽选择标准的优良性和可靠性。图2给出了整个金融系统的网络传染度随时间的变化趋势，根据式(19)得到。

表5 控制变量定义

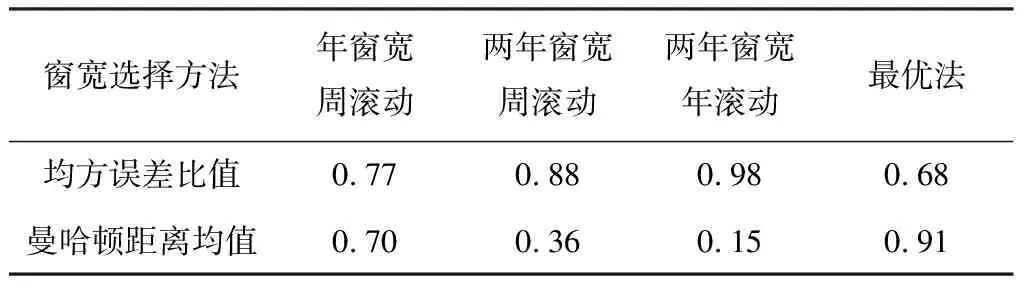
表6 金融网络结构模型的估计表现

比较表6中不同窗宽选择方法下模型的估计表现，得到的结论有：第一，当采用不同方法选择窗宽时，我国金融网络结构模型的估计表现差异较大。与最优法相比，以一年、两年等时间截点选择窗宽时，Bootstrap均方误差较大，说明模型的估计量表现差；曼哈顿距离值较小，说明参数随时间的变化情况相对较小。这可能导致的后果是无法捕捉到关键结构突变点；第二，采用最优法选择滚动窗宽时，Bootstrap均方误差值较小，曼哈顿距离值较高。这说明，本文方法能够兼顾两相悖目标：既能捕捉网络结构的结构突变性，也能使参数估计量的表现较优，优化了金融网络的结构突变识别过程。

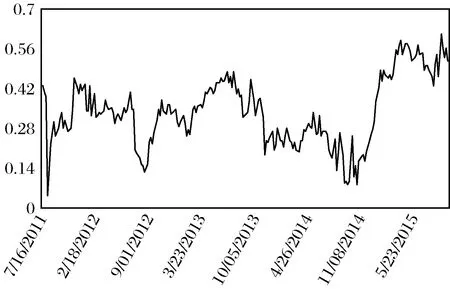
图2 整个金融系统的网络传染度的时间变化趋势图

由图2可以看出，网络传染度随时间的变化趋势明显，2011年至2012年呈现出小幅上升后回落的趋势，这与2012年上半年希腊危机，我国加快利率、汇率等市场化改革等有关。在2013年间，利率市场化进程加快，各大银行激烈竞争增加了中小银行的竞争成本，随之出现的“钱荒”问题也突显了银行系统面临的短期流动性问题，使得这期间金融系统的网络传染度水平攀升。随后由于宏观政策的调控，网络传染度有一定回落。而2015年上半年的股市出现较大波动，产能过剩问题不断升温，导致2015年间的金融系统网络传染度不断升高，经政府的不断注资和出台相应的调控政策，金融系统网络传染度逐渐回落但仍然处于一个相对高位。可见，当出现政策冲击，市场冲击，风险蔓延等事件时，金融系统的网络传染度会出现拐点，并呈现剧烈波动现象，说明本文的最优窗宽选择标准能够捕捉到金融网络的结构突变，从实证上证明了本文方法的有效性。

5 结语

本文针对时变参数模型，提供了一种可行的窗宽选择方法，具有理论意义和实践意义。蒙特卡罗模拟实验表明：第一，Bootstrap近似均方误差能够替代真实均方误差；第二，使用本文提出的最优窗宽选择法得到的模型估计量优于全样本序列得到的模型估计量，当参数出现连续断点时，本文的方法更有效；第三，在线性框架下，最优窗宽选择方法的估计表现优于以预测为目的的窗宽选择方法，说明了不能直接将以预测精度为目的的窗宽选择标准用于以捕捉参数结构突变为目的的模型中。第四，本文的方法适用于线性关系和非线性关系下的时变参数模型，且能拓展至常见的线性回归模型和广义线性回归模型中。实证检验表明，本文的方法能够优化金融网络的结构突变识别过程，弥补了当前在该领域中缺乏统计标准选择滚动窗宽的空白。