竞争中的参考价格效应及承诺

周尔凤，张廷龙，倪 蕾，方 丹，方 昶

(安徽师范大学经济管理学院，安徽 芜湖 241000)

1 引言

根据Kahneman和Tversky于1991年提出的前景理论，在消费者做出购买决策之前，他们对将要购买的产品会有一个心理估价，然后将这个心理估价与产品的真实零售价进行对比—如果心理估价要大于产品真实的零售价，那么消费者存在额外的交易效用，并因而更可能做出购买该产品的决策；反之，若产品零售价要高于该心理估价，消费者更可能放弃购买该产品，导致产品销量下降。学者们将这种心理估价称为参考价格，把其对销量的这种影响称为参考价格效应。关于参考价格的形成因素，Mazumdaret等[3]则认为除了价格之外，广告投入量、产品的质量、服务水平以及购物环境等因素也会影响消费者对产品的心理估价。皮德萍和胡燕娟[10]将参考效应引入到闭环供应链协调机制研究中，分析了其对两种不同闭环供应链的影响。Zhang Juan等[7]研究了一个由制造商和零售商构成的供应链系统，探讨了参考价格效应对广告和价格策略的影响。另外，由于电子商务的兴起，许多制造商通过传统零售渠道销售产品的同时还开辟了网上直销渠道，此时两个渠道上的价格互为参考，并对消费者决策产生影响，赵礼强和徐家旺[13]和曹晓刚等[8]探讨了双渠道下供应链的定价及协调决策等。王亮和王应明[12]基于前景理论的参考点效应，探讨了应对突发事件的决策方法。基于类似的理论，郝晶晶等[9]建立了基于前景理论的多阶段随机多准则决策分析框架，并提出了一种基于阶段发展特征的动态参考点设置方法。另外，与本文相关的文献研究还包括：张廷龙和梁樑[14]指出消费者购买决策还会受到诸如广告等销售努力行为的影响，他们在考虑零售商销售努力影响需求的情况下，探讨了不同渠道权力结构和信息结构下供应链的分散决策；何丽红等[9]在两层供应链中，考虑需求受广告努力水平和制造商提供的直接价格折扣的联合影响，建立了供应链成员的合作广告努力水平与价格折扣策略模型，并指出当制造商给予消费者最优直接价格折扣时，制造商和零售商的广告努力积极性与价格弹性正相关。

从企业的角度来看，广告是企业向消费者传递信息的一种有效方式，通过沟通产销信息，从而促进产品的销售。广告在企业开拓市场，争夺份额，创造经济效益等方面的作用不可忽视，是企业竞争战略中不可或缺的手段。对于广告投入决策，我们了解到许多企业会在财政年初或新产品投入市场的时候公布一个广告预算，Fairhurst等[1]指出，大概有16%的服务性企业都会公布他们的广告预算；Mitchell[5]研究了英国的制造业，发现27%的制造商会在财政年初或新产品投入市场之初宣布他们的广告投入量—如佳洁士在其一款新产品投入市场的时候，就宣布了要为该产品投入的广告预算。事实上，通过公布或承诺其广告投入，不仅可以让竞争双方都会了解彼此的广告投入以更好地做出各自的定价决策，同时也会对消费者对产品的参考价格产生影响。

另一方面，随着产品种类及品牌的日益增加，许多企业在节假日会有促销活动，消费者越来越聪明，他们会结合产品在不同阶段的价格来决定产品的购买时机及购买决策。面对消费者的这种战略行为，我们提出了价格承诺，即向消费者承诺价格在未来一段时间内或一直保持不变的话，那么在这个期间需要该产品的顾客就不会延迟他们的购买计划，从而促进该时期的销量及利润增长。Su Xuanming和Zhang Fuqiang[6]在供应链的环境下研究了价格承诺与数量承诺的问题，并指出在一些情况下，价格承诺会增加制造商、零售商的利润，而本文将在一个相互竞争的环境下研究价格承诺对利润的影响。

本文在竞争的环境下建立一个关于参考价格的模型，考虑市场上的两个企业是对称的，并从广告承诺及价格承诺的角度，寻求使企业长期利润最大化的广告及定价策略。我们分析了三种情形：双方都选择价格承诺、一方选择价格承诺，而另一方选择广告承诺、双方都选择广告承诺。首先分别研究了在这三种策略下参考价格效应对价格和广告投入的影响，然后通过数值分析，研究了各种参数的变化对利润的影响情况，并指出在不同情况下应该选择的最优策略。

2 模型建立

考虑市场中存在两个生产和销售同类产品的竞争企业1和2，他们需要在参考价格效应存在的背景下，思考各自的广告投放和定价策略决策。其中，为了减少竞争，每个企业将在价格承诺和广告投承诺等两个策略中进行选择。记ui(t)为企业i在t时刻的广告努力水平，pi(t)为企业i在t时刻的零售价格。一旦企业i选择价格承诺，其价格pi(t)将在整个销售季节保持不变；反之，若企业i选择广告承诺，其广告投入ui(t)也将是一个常数。由于价格承诺和广告承诺等两个策略是企业无任何承诺的特殊情形，因此本节在建模过程中暂时在一个更通用的框架下进行，即并不假定pi(t)和ui(t)固定不变。

为了描述参考价格效应，和先前文献Zhang Juan等[7]一样，本文采用以记忆和刺激相结合为基础的参考价格模型，假设产品i的参考价格ri(t)之变化服从以下动态方程:

ri(0)=ri0

(1)

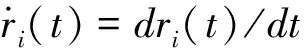
Si(t)=ai0-bipi+γi(ri-pi)+θipj,j≠i

(2)

其中,Si(t)为产品i在t时刻的销量，ai0表示产品i的潜在市场，pj(t)为竞争产品j在t时刻的零售价格，γi表示消费者对i企业产品参考价格与零售价之间差异的敏感性，即参考价格效应对i企业销量的影响程度，bi为消费者对i企业产品零售价格的敏感程度，θi表示j企业的产品对i企业产品的替代程度。

至于广告成本，我们参考Zhang Juan等[7]，假设广告成本与广告努力水平之间成平方关系，即:

(3)

为了便于计算，本文进行以下假设：(1)销售季节无限长；(2)两个企业实力相当，相关参数是对称的，即αi=α，βi=β，ri0=r0，ai0=a0，γi=γ，bi=b，θi=θ；(3)生产成本为零。

因此，企业i在时刻t的利润为:

πi(t)=pi(t)Si(t)-C(ui(t))

(4)

其决策目标为:

(5)

其中，Ji是企业i利润在时刻t=0的净现值，ρ为贴现率。两个企业需要在满足式(1)中的约束条件下，最大化各自的利润净现值。

3 双头垄断博弈均衡

针对两个企业所有可能的策略组合，我们在本节分别分析三种不同的策略情形，即：(1)双方都选择价格承诺；(2)一方选择价格承诺，而另一方选择广告承诺；(3)双方都选择广告承诺。

3.1 双方都选择价格承诺

当双方都做出价格承诺时，他们的价格将不再随时间变化。这时，两个企业的决策顺序如下。首先在时刻t=0, 双方独立地在不知道对方决策的情况下选择各自的零售价格p1和p2；然后，两个企业根据p1，p2和当前的市场情况，动态地决定各自在时刻t的广告投入。出于方便我们用下标“pp”记该情形下的均衡决策。

给定p1和p2,两个企业的决策问题可简化为：

(6)

ri(0)=ri0

命题3.1给出固定p1和p2时两个企业动态博弈下的开环博弈均衡解。

命题3.1：当两企业都选择价格承诺策略且给定p1和p2时，两个企业的均衡广告投入为：

ui(t)=Npi,i=1,2

产品i参考价格随时间的变化情况为：

ri(t)=M1i+(ri0-M1i)e-αt

其中N=γβ/(ρ+α),M1i={1+βN/α}pi均为常数。

命题3.2：在Stackelberg博弈框架及双方都选择价格承诺的情况下，两企业均衡的广告努力水平、零售价格和利润如表1所示。

表1 双方选择价格承诺情况下的广告水平、价格和利润

其中N=γβ/(ρ+α)，n1=1+γβ2/(α(ρ+α))，F=(γβ2(1-2α(ρ+α))+2(ρ+α)2(b+γ-γα2))/((ρ+α)2ρ)，为确保pipp>0，则ρF-θ>0要满足。

对pipp求关于a0和r0的导数可得到下面的结论：∂pipp/∂a0>0，∂pipp/∂r0>0，也即初始市场占有量或初始参考价格越高，产品的零售价格就越高。

将pipp代入到ri(t)=M1i+(r0-M1i)e-αt中，可得到稳定的参考价格：

rippss=

(7)

对rippss求关于a0和r0的导数可得到下面的结论：∂rippss/∂a0>0，∂rippss/∂r0>0，也即初始市场占有量或初始参考价格越高，稳定的参考价格就越高。另外，通过比较稳定的参考价格和零售价格，我们发现rippss恒大于pipp，即稳定的参考价格恒大于承诺的固定价格，因此我们可以推断，在某一时期之后，参考价格效应会对销量产生一个正的促进作用。

将pipp代入到命题3.1中，得到：

(8)

对uipp求关于pipp的导数即可得到∂uipp/∂pipp>0，即越高的零售价格会刺激企业投入更多的广告，来增加产品在消费者心中的价值；对uipp求关于γ的导数即可得到 ∂uipp/∂γ>0，即消费者对参考价格与零售价格之间的差异越敏感，那么企业投入的广告量也会越高，这主要是因为广告可以通过提高产品在消费者心中的价值，即参考价格，从而增加销量。另一方面，γ越大，通过增大广告投入，销量增加的程度也越大。

3.2 一方选择价格承诺，而另一方选择广告承诺

当一方选择价格承诺，而另一方选择广告承诺时，用1来标记选择价格承诺的企业，用2来标记选择广告承诺的企业。这时，企业1的价格将不随时间变化，企业2的广告努力水平将不随时间变化。这时，两个企业的决策顺序如下。首先在时刻t=0, 企业1和企业2在不知道对方决策的情况下分别选择各自的零售价格p1和广告努力水平u2；然后，两个企业根据p1，u2和当前的市场情况，动态地决定各自在时刻t的广告投入u1和零售价格p2。出于方便我们用下标“pu”记该情形下的均衡决策。

给定p1和u2,两个企业的决策问题可简化为：

(9)

(10)

命题3.3：当企业1选择价格承诺，企业2选择广告承诺的策略下，且给定p1和u2时，两个企业的均衡广告努力水平u1和零售价格p2分别为：

u1(t)=u1ss=Np1

p2(t)=E1eA1t+B1

产品i参考价格随时间的变化情况为：

r1(t)=M2+(r0-M2)e-αt

r2(t)=M3+(r0-M3)eA1t

其中A1,M2,M3,N,B1=p2ss,E1,c,d,g均为常数。

对p2ss求关于β，θ及b的导数可得到：∂p2ss/∂β>0，∂p2ss/∂θ>0，∂p2ss/∂b<0。首先，因为广告对品牌形象有正的促进作用，对于同一单位的广告投入，若β越大(即广告效率越高)，则消费者对产品的参考价格就提高得越快，同时也会带动零售价格的提高，从而稳定的零售价格也越高。其次，θ越大，即产品之间的替代性越大，促使对方的零售价格对我方销量的影响越大，并且对我方销量是一种正的促进作用，因此也会促进稳定零售价格的提高。最后，b反映的是消费者对产品零售价格的敏感程度，b越大，即消费者越容易受价格波动的影响，从而导致稳定的零售价格越低。另外，稳定的参考价格恒大于稳定的零售价格。这主要是由于广告会对参考价格有一个正的促进作用。

命题3.4：在Stackelberg博弈框架及企业1选择价格承诺，而企业2选择广告承诺的情况下，两企业均衡的广告努力水平、零售价格和利润如表3.2所示。

表2 混合情况下的各变量值

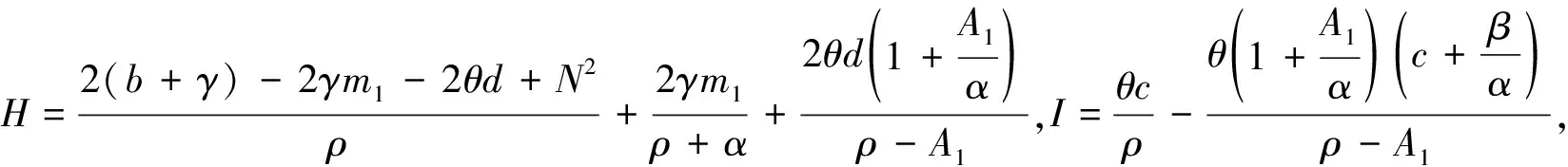
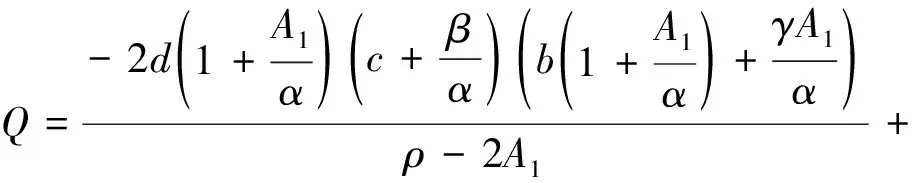
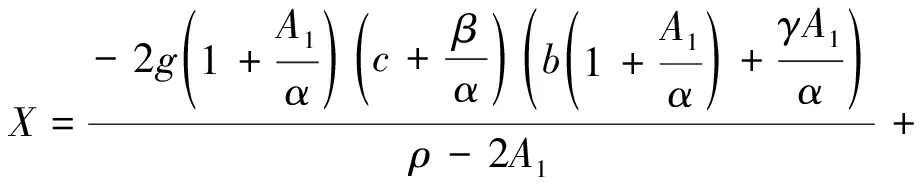
对u1pu,p1pu,u2pu,p2pu求关于a0和r0的导数，我们可以发现a0和r0对企业1广告投入和价格的影响趋势是相同的，而影响趋势是正相关或负相关则取决于相关参数的大小。另外，当消费者对参考价格与零售价格之间的差异越敏感(即γ越大)或广告努力对参考价格的影响程度越大(即β越大)时，广告投入水平受价格的影响也就越大。而当价格差异对参考价格变化速率的影响越大(即α越大)时，广告投入水平受价格的影响则越小。结合命题3.3的结论，我们发现当初始参考价格低于稳定的参考价格(即r0

3.3 双方都选择广告承诺

当双方都做出广告承诺时，他们的广告努力水平将不再随时间变化。这时，两个企业的决策顺序如下。首先在时刻t=0, 双方独立地在不知道对方决策的情况下选择各自的广告投入水平u1和u2；然后，两个企业根据u1，u2和当前的市场情况，动态地决定各自在时刻t的零售价格。出于方便我们用下标“uu”记该情形下的均衡决策。

给定u1和u2,两个企业的决策问题可简化为：

(11)

命题3.5：当两企业都选择价格承诺策略且给定u1和u2时，两个企业的均衡零售价格为：

pi(t)=E2eA2t+B2

产品i参考价格随时间的变化情况为：

ri(t)=M4i+(r0-M4i)eA2t

其中A2,B2,M4i,E2i,k,l均为常数。

命题3.6：在Stackelberg博弈框架及两企业都选择广告承诺的策略下，两企业均衡的广告努力水平、零售价格和利润如下表3所示。

表3 双方选择广告承诺情况下的各变量值

因为A2piuuss+βui/α，会导致一个价格战的恶性循环，当一方降低价格时，会引导另一方把零售价格降得更低，最后，双方可能发现，它们可能获得了相当的销量，但是以更低的价格及边际利润为代价的。若ro>piuuss+βui/α，此时两企业采取的均为渗透定价的策略，当企业2增加其零售价格时，同时会增加企业1的销量，考虑到企业2零售价格的影响，企业1会更快地增加其零售价格来适应企业2的策略。

其中：

A2=0.5(ρ-

T=(b+γ-θ)

4 数值分析

在本节，我们将采用数值分析的方法来比较不同情况下企业1的利润大小(因为两企业是对称的，所以企业2的利润也是相同的)，具体分析参数γ，θ，b，α及β的变化对利润的影响。首先，我们定义情形ij，i=1表示企业2选择价格承诺，i=2表示企业2选择广告承诺，j=1表示企业1选择价格承诺，j=2表示企业1选择广告承诺，情形ij则表示在企业2选择i决策的时候，企业1选择j决策。本文使用的参数值分别为：a0=300，r0=10，γ=1，θ=5,b=8,ρ=0.1,α=0.5,β=0.5，通过变动γ，θ，b，α及β的值来分析其对利润的影响情况。

4.1 消费者对参考价格与零售价格之间差异的敏感程度

如图1所示，在给定的范围内，J1会随着γ的增大而增大，J2而会随着γ的增大而降低。这主要是因为在双方都选择价格承诺时，企业1的零售价格是不变的，参考价格的变化率是固定的，并且在本例给的数值下是正数，从而会刺激销量增长，因此企业1的利润会随着γ的增大而增大。而对于J2，在此情况下，企业1的价格及销量均是变动的，都会受到参考价格效应及消费者对参考价格与零售价格之间差异的敏感程度(γ)的共同影响，其综合结果导致企业1的利润随γ的增加而降低。

图1 情形11及12中γ对利润的影响

从图2中可以看到，在企业2选择广告承诺的情况下，企业1选择价格承诺的利润(J1)变化趋势与企业1选择广告承诺的利润(J2)变化趋势相似，均为先下降后上升。这主要是因为当γ很小的时候，与企业1的参考价格效应相比，由企业2引起的替代效应占主导，并且在γ很小时，企业2的价格会随着γ的增大而变化，其综合结果导致企业1的利润下降。当γ超过某一临界值时，企业1的参考价格效应及企业2的替代效应的综合结果导致企业1的利润随γ的增大而增大。同时，从图4.2中还可以看出，J2的变化速度要高于J1的变化速度。

图2 情形21及22中γ对利润的影响

4.2 产品之间的替代程度

如图3所示，企业1的利润在这两种情况下的变化趋势是相似的，均以恒定的速率上升，原因很简单，在竞争对手选择价格承诺的情况下，企业2的价格是不变的，那么企业2的价格对企业1销量的影响(θp2)则会随着θ的增大而增大，从而导致企业1的利润随θ的增大而增大。所不同的是，在企业1选择广告承诺的情况下利润的上升速度要高于选择价格承诺的情况。

图3 情形11及12中θ对利润的影响

从图4中可以看出，在竞争对手(企业2)选择广告承诺的情况下，企业1在选择价格承诺及广告承诺下的利润均呈上升趋势，且企业1在选择广告承诺下的利润上升速度要高于选择价格承诺的情形。

图4 情形21及22中θ对利润的影响

4.3 消费者对零售价格的敏感程度

如图5所示，在情形11下，J1受b的影响较小。由于在这种情形下，对方及自己的价格均保持不变，以及b变化较小，所以J1的变化较小。在情形12中，J2随h的增大而上下波动，这主要是因为我方选择了固定广告的策略，价格随时间变化，利润同时受到参考价格效应、零售价格、替代效应的共同影响，从而导致J2随b的增大而变化较大。并且从图中可以看出，当竞争对手选择固定价格策略，且b较小时，选择固定广告是我方最优的决策。从图6可看出，在情形21中，J1会随着b的增大而减小，而在情形22中，J2随b的增大而增大，但增大的幅度较小。

图5 情形11及12中b对利润的影响

图6 情形21及22中b对利润的影响

4.4 产品过去价格对参考价格的影响程度

如图7所示，在情形11下，企业1的利润会随着α的增大而下降，而在情形12中，企业1的利润先上升后下降。如图8所示，当竞争对手(企业2)选择广告承诺时，企业1在价格承诺及广告承诺两种策略下的利润均呈下降的趋势。

图7 情形11及12中α对利润的影响

图8 情形21及22中α对利润的影响

4.5 广告对参考价格的影响程度

如图9所示，J1会随着β的增大而增大，而J2随着β的增大先下降后上升。对于情形11，由于企业1的广告投入会随着β的增大而增大，从而对参考价格产生正的影响，刺激销量，导致企业1的利润会随着β的增大而增大。而在情形12中，企业2选择价格承诺，β不仅会对广告投入量产生影响，同时也会对产品零售价格及参考价格产生影响，那么这些因素的综合结果则导致了图中J2的变化趋势。

如图10所示，在情形21中，利润的变化趋势与情形11是类似的，均随着β的增大而增大。而在情形22 中，企业1的利润随着β的增大先上升后下降，其影响因素与图9中的类似，只不过在图10中，竞争对手(企业2)选择广告承诺，那么为了应对竞争对手的策略，企业1的最优决策也会作相应的调整来适应对方，以使自己的长期利润最大化。

图9 情形11及12中β对利润的影响

图10 情形21及22中β对利润的影响

5 结语

本文在考虑消费者参考价格效应的情况下，提出了两种策略，即广告承诺和价格承诺，同时考虑了竞争对手的策略对我方最优策略选择的影响。通过最优控制的方法，得到了三种不同情况下的均衡解。

本文的研究结果发现：首先，稳定的参考价格总是要高于稳定的零售价格，这主要是由于广告会对参考价格产生一个正的影响；其次，在双方都固定广告的情况下，价格的变化速度要高于一方固定广告而另一方固定价格的情形。并且当初始的参考价格很高时，前一种情况下价格下降的速度要高于后一种情况，这主要是由于双方都选择广告承诺，而进行价格战的结果；当初始的参考价格很低时，前一种情况下价格上升的速度要高于后一种情况，这主要是由于竞争产品之间的替代性，竞争对手的价格会对我的销量产生正的影响，在初始的参考价格很低的情形下，对方采取一种渗透定价的策略，同时也会刺激我方销量的增长及价格的快速上升，这主要是考虑(适应)对方策略的结果；最后，我们采用了数值分析的方法，发现价格承诺在一些情况下要优于广告承诺，而在另一些情形下，广告承诺则更优。

附录：

命题3.1的证明

在动态环境下，两企业要确定最优的广告投入水平，我们通过哈密尔顿方程求解最优控制问题。首先构造企业i的现值哈密尔顿函数Hi：

(A.1)

给定价格，企业最优控制问题的必要条件为：

(A.2)

(A.3)

化简(A.2)得到

-ui+βλi=0,ui=βλi

(A.4)

对(A.4)等式的两边求一阶导得到：

(A.5)

将(A.3)代入(A.5)中可得：

(A.6)

求解等式(A.6)的微分方程，可得到企业i的最优广告投入水平的通解为：

ui(t)=C1e(ρ+α)t+uiss

(A.7)

其中uiss=Npi，N=γβ/(ρ+α)。C1为需要确定的常数，为求得C1，我们假设ri(t)=M1i+(r0-M1i)e-m1t，ri(t)对t求一阶导得到：

(A.8)

(A.9)

解上面的方程，我们得到两个解：

解一：m1=ρ+α，M1i=(1+γβ2/(α(ρ+α)))p1，C1=(ρ+2α)(r0-M1i)/β；解二：m1=-α，M1i=(1+γβ2/(α(ρ+α)))p1，C1=0。

ui(t)=uiss=Npi

(A.10)

命题3.2的证明

将命题3.1的结果代入式(3.6)，我们得到了企业i在价格p1，p2下的利润函数，利润Ji对价格pi求一阶导，并根据利润最大化的条件，令∂Ji/∂pi=0，得到：

(A.11)

命题3.3的证明

在动态环境下，企业1为决策最优的广告投入水平，企业2为决策最优的价格，首先构造两企业的现值哈密尔顿函数H1，H2：

(B.1)

(B.2)

对于给定企业1的价格和企业2的广告投入水平，企业1最优控制问题的必要条件为：

(B.3)

按照命题3.1类似的求解步骤可得到企业1最优的广告投入水平及参考价格随时间的变化函数：

(B.4)

r1(t)=M2+(r0-M2)e-αt

(B.5)

对于给定企业1的价格和企业2的广告投入水平，企业2最优控制问题的必要条件为：

(B.6)

(B.7)

化简等式(B.6)可得：

(B.8)

化简得：

(B.9)

首先，在等式(B.9)中求解p2关于时间t的一阶导数并代入(B.7)中的结果，然后再对等式的左右两边同时求关于t的微分并再次代入(B.7)中的结果得到：

(B.10)

求解等式(B.10)的微分方程可得到企业2最优的价格：

p2(t)=E0eA0t+E1eA1t+B1

(B.11)

其中E0，E1为需要确定的常数。类似于命题4.1的证明，我们得到均衡的价格为：

p2(t)=E1eA1t+B1

(B.12)

另外，为求得E1，我们设

r2(t)=M3+(r0-M3)e-m2t

(B.13)

r2(t)对时间t求一阶导得到：

(B.14)

α(p2(t)-r2(t))+βu2=α(E1eA1t+B1-M3-(r0-M3)em2t)+βu2

(B.15)

解上述方程得到：

命题3.4的证明

采用逆推法来求出企业1最优的固定价格，将命题3.3中的结果代入到利润函数(3.9)中，利润J1对价格p1求一阶导，并根据利润最大化的条件，令∂J1/∂p1=0得到：

(B.16)

其中I,J,K,H均为常数。

采用类似的方法，我们可以得到命题3.4的结论。