基于改进多目标粒子群优化算法的企业再制造物流网络优化
2018-09-08程发新程显钦王广东
李 莉,程发新+,程显钦,王广东,潘 婷
(1.江苏大学 管理学院,江苏 镇江 212013; 2.东北林业大学 信息与计算机工程学院,黑龙江 哈尔滨 150040; 3.枣庄中联水泥有限公司,山东 枣庄 277143)
0 引言
随着资源和环境约束的不断加强,企业再制造已经成为顺应低碳循环经济发展的必然趋势。作为企业实施再制造的基础,再制造物流网络优化规划的合理性从根本上决定了企业再制造的效率和效益,已经受到学术界的重视。企业作为盈利性实体,追求经济绩效是企业再制造的首要目标[1]。为此,许多学者以经济绩效最优为目标,从不同视角优化企业再制造物流网络,并取得了丰硕的研究成果[2-4]。
在寻求经济目标最优的同时,企业再制造物流网络运作过程中的碳排放也不容忽视。为了将企业二氧化碳排放的负外部性内部化,采用以价格控制为特征的市场机制手段对碳排放征税受到发达国家的推崇[5]。碳税具有价格信号明确、实施成本较低等优势[6],因此中国政府预计将于2020年开征碳税。在碳税政策下,企业需要整合供应链上下游节点开设、物流量分配和运输方式的选择,合理规划物流网络资源,从而在降低成本的同时实现碳减排。作为与再制造物流相关的供应链物流网络优化研究,已有学者以成本和碳排放最小化为目标,研究多目标供应链物流网络优化问题,但现有研究尚存一些不足:①相关研究仅在目标函数中考虑碳排放的影响,未将碳税政策纳入多目标物流网络的优化。例如,Fan等[7]提出总成本和二氧化碳最小化的供应链网络优化模型,旨在通过提高网络节点容量和增加供应设施来权衡成本和碳排放;Ruimin等[8]以成本和碳排放最小化为目标,建立规划模型以优化闭环供应链物流网络。②在多目标物流网络优化过程中,相关学者仅考虑节点设施选址或运输方式优化[9],而这种将选址和运输分离的优化方式将会产生双边际效应,降低供应链的整体绩效。高举红等[10]为解决物流网络设施选址、开设数量与设施间的物流量分配问题,建立了双目标混合整数规划模型,以提高物流网络运营效率;何其超等[11]考虑政府和企业两方需求建立多目标规划模型,比较分析了运输方式对物流网络成本和碳排放量的影响。事实上,不同运输方式会使再制造物流网络各节点间的运输距离不同。为实现再制造物流网络的整体效益,在考虑再制造物流网络节点选址的同时,需综合协调各设施间物流运输方式的运营成本与碳排放量,从而获得多目标企业再制造物流网络优化模型的最优解。
随着企业再制造物流网络优化研究的逐渐深入,多数学者仅着眼于模型构建,从单一目标向多目标模型探索,鲜有学者从算法角度出发,在增加模型复杂度的同时对求解算法进行探索改进。目前,大部分文献对多目标优化模型的求解仍滞留在传统的多目标优化方法,这里存在以下两个问题:
(1)传统多目标优化方法将多目标问题转化为单目标问题求解,其搜索结果局限于单值最优解[12]。例如,何其超等[11]采用加权法求解多目标优化问题,将多目标优化问题转换为总成本最小的规划问题,获得了单点最优解。然而,多目标优化问题与单目标优化问题的本质区别在于其解并非唯一,必然存在一组由多个非劣解组成的Pareto最优解集[13]。Ghaybloo等[14]为得到Pareto最优解集,结合权重法和约束法将利润和绿色度转化为单一目标向量,通过在[0,1]区间内不断调试权重向量获得相应最优解,最后整合不同权重向量对应的最优解合成Pareto最优解集,然而该方法需要根据权重向量不断调试,且算法的搜索结果在很大程度上依赖于权重值的选择,主观性较强。相比而言,多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法采用高效的集群并行计算方式搜索,优化结果不限于单值解,而是一次运行中就能获得Pareto最优解集[15]。因此,文中采用MOPSO算法求解多目标物流网络优化模型。
(2)将MOPSO算法引入多目标优化问题时需要结合具体问题设计约束处理机制。这是由于规划模型算法的有效性与每类问题的特有属性密切相关[16],约束条件是多目标物流网络优化问题不可或缺的一部分,而进化算法本质上是一种无约束优化方法[17],因此需要结合具体问题对MOPSO算法改进,以便提高其在实践中的应用价值。
鉴于此,文中首先在碳税政策下以成本和碳排放最小化为目标构建混合整数规划模型。其次,结合多目标再制造物流网络优化问题,编码约束处理机制,设计改进的多目标粒子群优化 (Modified Multi-Objective Particle Swarm Optimization, MMOPSO) 算法。最后,结合ZL水泥企业具体运营管理数据进一步优化企业再制造物流网络结构,验证MMOPSO算法在实践应用中的有效性。同时,在小、中、大3种不同问题规模下,比较MMOPSO算法与第二代约束非支配排序遗传算法(Constrained Non-dominated Sorting Genetic Algorithm Ⅱ,CNSGA-Ⅱ)的性能。相对于现有多目标企业再制造物流网络优化研究,本文的主要贡献如下:①将碳税政策引入多目标企业再制造物流网络优化,在碳税政策下获得总成本和碳排放的最优解;②在企业再制造物流网络节点选址的同时,充分考虑各种运输方式优势,使企业再制造物流网络总成本和碳排放最小,以弥补传统选址与运输分离的物流网络优化方式导致的双边际效应;③设计约束处理机制改进MOPSO算法,并与CNSGA-Ⅱ算法的性能进行比较,以体现MMOPSO算法在求解中、大规模问题应用中的优势。
1 模型的建立
根据研究问题,文中建立多目标混合整数规划模型,综合协调企业再制造物流网络上下游节点开设、物流量分配和运输方式的选择,旨在实现企业再制造物流网络总成本和碳排放目标最小化。
1.1 模型描述
文中拟建立一个包括第三方回收商、供应商、再制造商、分销商和销售商的开环再制造物流网络,如图1所示。其运作过程主要为:①在逆向物流中,第三方回收商对废旧产品分类回收、加工处理、检测后,将可再制造的部分供应给再制造商,再制造商将可再制造料分类检测,以保证其可再制造性;②在正向物流中,供应商向再制造商提供产品生产原材料,再制造商将原材料和可再制造料按一定比例掺加进行再制造,并将再制造产品分发给分销商,分销商将再制造产品授权给销售商向市场销售。

1.2 模型假设
结合本文研究问题,在不改变问题实质的前提下,对一些复杂的条件进行简化,并提出一些基本假设:
(1)假设企业再制造逆向物流中存在R个备选第三方回收商(r=1,2,…,R),正向物流中存在S个备选供应商(s=1,2,…,S)、M个备选再制造商(m=1,2,…,M)、D个备选分销商(d=1,2,…,D)和C个销售商(c=1,2,…,C),以此为节点构成企业再制造开环供应链网络。其中,销售商的位置固定,不考虑其设施选址成本。
(2)根据企业再制造逆向物流的特有属性,第三方回收商向再制造商的运输过程中只考虑公路运输。在正向物流中,可根据实际情况选择公路、铁路、水路3种运输方式(t=1,2,…,T)组合完成运输任务,其运输能力存在限制,用Capt表示。
(3)各个备选节点的处理能力有限。Capr,Caps,Capm,Capd分别表示各个备选第三方回收商、备选供应商、备选再制造商和备选分销商处理能力的上限。
(4)假设政府部门对企业再制造碳排放量按P元/t征税,随着碳税税率的变化,再制造商考虑是否投入减排技术h(h=1,2,…,H)进行碳减排。
1.3 模型构建
从模型描述和假设出发,构建碳税政策下总成本和碳排放最小化的混合整数规划模型,旨在降低企业总成本的同时减少二氧化碳排放量。
1.3.1 目标函数确定
(1)企业再制造物流网络优化的首要目标为总成本最小化。总成本(C)由固定建设成本(FC)、可变成本(AC)、运输成本(TC)和碳税成本(Tax)构成,其目标函数为
minC=FC+AC+TC+Tax。
(1)
固定成本包括若干第三方回收商、供应商、再制造商和分销商建设的固定成本(FIr,FIs,FIm,FId),及其是否开设的决策变量(Xr,Ys,Zm,fId)的乘积之和与销售商的固定成本FIc加总构成:
(2)
可变成本由各个节点运作成本加总构成:
(3)
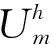
运输成本由3种运输方式在已开设的各节点间的运输固定租赁成本和运输可变成本加总构成:
(4)
式中:TF1,Vrm,TC1和Drm分别表示企业再制造逆向物流的公路外包固定租赁成本、是否在节点间建立运输、单位运输成本及运输距离;TFt,TCt分别表示企业再制造正向物流中租赁第t种运输方式的固定成本和单位运输成本;Vsmt,Vmdt,Vdct分别表示各节点之间是否采用第t种运输方式的决策变量;Dsmt,Dmdt,Ddct分别表示各节点间之间采用第t种运输方式的运输距离。
碳税政策下,政府对企业直接碳排放(ACOE)和间接碳排放(MCOE)依据碳税税率P征税:
Tax=P×(ACOE+MCOE)。
(5)
(2)企业再制造物流网络优化的另一个目标为碳排放量最小化。碳排放量由直接碳排放和间接碳排放构成:
minE=ACOE+MCOE。
(6)
直接碳排放由再制造商生产再制造产品的碳排放以及各节点间运输产生的碳排放总量抵扣采用技术h的碳减排量构成:
(7)

间接碳排放由各节点运作过程中消耗的单位电能Er,Es,Em,Ed,Ec与各个节点间物流量以及电力碳排放因子WE的乘积加总构成:
(8)
1.3.2 约束条件
根据企业再制造的现实情况,需在流量约束、容量约束和决策变量约束范围内搜索可行解,从而寻求成本和碳排放目标的最小化。
∀r;
(9)
∀m;
(10)

(11)

(12)
Qrm≤Cap1,∀r,m;
(13)
Qsmt≤CaptVsmt,∀s,m,t;
(14)
Qmdt≤CaptVmdt,∀m,d,t;
(15)
Qdct≤CaptVdct,∀d,c,t;
(16)

(17)

(18)
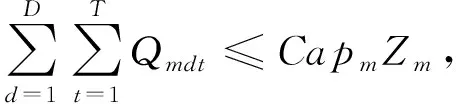
(19)

(20)
Xr,Ys,Zm,Id∈{0,1},∀r,s,m,d;
(21)
Vrm,Vsmt,Vmdt,Vdct∈{0,1},∀r,s,m,d,c,t;
(22)
∀r,s,m,d,c;
(23)
Qrm,Qsmt,Qmdt,Qdct≥0,∀r,s,m,d,c,t;
(24)

(25)
式(9)~式(12)表示企业再制造物流网络各设施流量均衡约束,其中α为废旧产品的可再制造率,δ表示可再制造料与原材料的掺合比率,β表示掺合料转化为再制造产品的比率;式(13)~式(16)表示不同运输方式在各节点间运输的能力限制;式(17)~式(20)表示物流网络各节点最大运作容量约束;式(21)~式(25)表示决策变量的取值范围。
2 多目标粒子群优化算法
粒子群算法源于对鸟类捕食行为的研究,算法中每个粒子的位置代表优化问题的一个潜在解。B维搜索空间中由N个粒子组成种群,每个粒子i包含B维的位置向量Xi=(Xi1,Xi2,…,XiB)T和速度向量Vi=(Vi1,Vi2,…,ViB)T。在搜索过程中,粒子记住其搜索到的历史最优位置Pi=(Pi1,Pi2,…,PiB)T,然后在每次迭代中,根据其个体历史最优位置Pi和全局最优位置Pg=(Pg1,Pg2,…,PgB)T不断更新自身速度和位置,从而实现种群进化。第i个b维粒子的速度和位置更新公式如下[12]:
(26)
(27)
式中:k为当前迭代次数;c1和c2为加速度因子;ω为惯性权重;r1和r2为[0,1]间的随机数。
2.1 Pareto支配关系
传统多目标优化方法采用加权法,通过已知权重将多目标问题转化为单目标问题求解,其搜索结果局限于单值最优解。为克服传统多目标优化方法计算的局限性,文中采用基于Pareto支配关系的MMOPSO算法,在一次运行中就能求得Pareto最优解集。
为便于理解Pareto的支配关系,对其进行简单介绍。不失一般性,考虑以下具有n个决策变量和j个目标函数的多目标优化问题min(f1(x),f2(x),…,fj(x)),x=(x1,x2,…,xn)为n维决策向量,且x∈X,X为决策空间。向量xu支配向量xv(记为xuxv)当且仅当∀i∈{1,…,j}满足fi(xu)≤fi(xv),同时∃i∈{1,…,j}满足fi(xu) 文中提出的MMOPSO算法采用外部存档存储粒子每一代搜索到的非支配解,迭代结束时外部存档中的最终解即为多目标优化的Pareto最优解集。 外部存档中非劣解的存储方法具有以下两个特征[18]:①每次迭代中,要进入外部存档的解与外部存档中已存在的解具有支配关系,即将每一代获得的解与外部存档中已存在的解逐一比较,若该新解支配外部存档中已存在的解,则将该新解存入外部存档,删除外部存档中被新解支配的解;②外部存档中已存在的解之间互不支配,没有优劣之分。 粒子一旦存入外部存档,就没有优劣之分。而MOPSO算法需要解决的另一个问题是在每一代的外部存档中确定一个性能最好的解作为全局最优位置Pg,用于领导粒子进行搜索。外部存档中的解密度越低,解的分布性和算法全局搜索能力越好[18]。文中采用自适应网格法估计外部存档中解的密度信息,将外部存档划分为多个网格,作为全局最优位置的选择依据,具体步骤如下: 步骤3根据粒子对应的适应度值确定粒子所在网格的位置索引值idx,同时计算该网格中存放粒子的数量,网格中存放的粒子越少解的密度越低,选择密度最低的网格。 步骤4对于同一网格内的多个粒子,采用轮盘赌法从中随机选择全局最优位置Pg。 上文构建的多目标混合整数规划模型受流量约束、容量约束及运输能力约束条件的限制,模型求解过程中,需要在这些约束条件下寻求多目标优化问题的Pareto最优解集。MOPSO算法是一种无约束搜索机制,因此将MOPSO算法应用于约束多目标优化问题时,需要结合具体问题编码约束处理机制,设计MMOPSO算法。 MMOPSO算法在基本MOPSO算法基础上设计约束处理机制,通过流量分配算法、容量调整算法将约束条件编码成算法语言,在可行域内搜索。对于运输量超出运输能力限制的不可行解,采用运输能力限制转换算法,即对超出运输能力限制的不可行解构造惩罚函数,并将惩罚项作用于不可行解,经连续多次迭代进化,最终淘汰不可行解。 2.3.1 粒子编码规则 ∀d,c,t; (28) (29) 具体的编码思路为:Xib在粒子群算法空间内表示粒子群中第i个b维粒子的位置,亦表示多目标企业再制造物流网络优化问题的一个解。通过以下编码方法将多目标再制造物流网络优化问题的解空间映射到粒子群算法编码空间。 步骤1将分销商d至销售商c采用第t种运输的运输量Qdct重新排列为b1维向量x1,其中维度b1=D×C×T。 步骤2将再制造商m至分销商d采用第t种运输的运输量Qmdt重新排列为b2维向量x2,其中维度b2=M×D×T。 步骤3将供应商s至再制造商m采用第t种运输的运输量Qsmt重新排列为b3维向量x3,其中维度b3=S×M×T。 步骤4将第三方回收商r至再制造商m采用公路运输的运输量Qrm重新排列为b4维向量x4,其中维度b4=R×M。 步骤5将以上向量组合成Xib=[x1x2x3x4]T,Xib表示粒子群中第i个b维粒子的位置,则粒子维度b=b1+b2+b3+b4。 2.3.2 MMOPSO算法流程 (1)参数初始化 将种群规模设为60,最大迭代次数为100,外部存档容量为100,个体学习因子c1和种群学习因子c2都设为1.496,自适应扩张参数τ设为0.1。 (2)流量分配算法 为确定各个设施间的物流量,将流量约束条件(9)~(12)编码为算法语言进行表达,从而在各设施间选择成本和碳排放最低的运输方式分配物流量。 (1)将分销商到销售商的再制造产品运输量Qdct按照t种运输方式的运输成本和碳排放量进行排序,索引值越小,优先级越高。 (2)选择最优先的运输方式决定运输量,即Qdct=min(Capt,Demc),直到每个销售商的需求都被满足,转步骤2。 步骤5在确定物流量后,按照上文描述的编码规则将多目标优化问题的解空间映射到MMOPSO算法编码空间,从而获得粒子位置Xib,同时初始化粒子的搜索速度。 (3)容量调整算法 为使开设的各个设施在其能力范围内运营,将容量约束条件(17)~(20)转换为算法语言进行表达,从而选择开设成本和碳排放量最低的设施。 步骤2若已开设的分销商供应能力缺少量Cd>0,则将未开设分销商的运营成本和碳排放量排序,索引值越小的优先级越高,选择开设优先级最高的设施,否则不需要增设分销商。 步骤3再制造商、供应商、第三方回收商的容量调整方法亦如此,不再赘述。 (4)适应度值计算 适应度值计算分为两部分,将式(1)~式(5)所示的成本目标函数、式(6)~式(8)所示的碳排放目标函数用算法语言分别编码为适应度值。 (5)运输能力限制转换算法 为保证开设的各设施之间的运输量不超过运输承载能力,采用罚函数法将运输能力约束条件(13)~(16)进行转换,通过乘以罚函数Penalty来保证各运输方式的运输量不超出运输能力限制。 步骤1比较节点间超出各种运输能力限制的物流量Difrm=Qrm-Cap1,∀r,m;Difsmt=Qsmt-CaptVsmt,∀r,m,t;Difmdt=Qmdt-CaptVmdt,∀m,d,t;Difdct=Qdct-CaptVdct,∀d,c,t。 步骤2采用式(30)重新计算适应度值Fitness(j),其中j=1,2。对超出运输能力限制的物流量进行惩罚,用适应度值函数评价通过约束条件筛选出的所得解的优劣,在此基础上初始化粒子的个体最优值pi和全局最优值pg,判断粒子间的支配关系,初始化外部存档。 Fitness(j)=Fitness(j)+Penalty× (30) (6)更新粒子速度和位置 在保证粒子在搜索空间飞行的条件下,按照式(26)和式(27)分别更新粒子的速度和位置。由于惯性权重ω对粒子群优化算法的收敛性能有很大影响,为平衡粒子的全局搜索和局部搜索功能,根据式(31)改进惯性权重ω,使其随着迭代次数k增加至最大迭代次数MaxIter,ω值由初始惯性权重ωstart=0.9非线性递减至ωend=0.4。 ω(k)=ωstart-(ωstart-ωend)(k/MaxIter)2。 (31) (7)更新最优值 更新粒子的个最优位置pi,根据非劣解更新外部存档。构建自适应网格,确定外部存档中粒子在自适应网格中的位置,采用轮盘赌法选择领导粒子,更新种群最优位置pg。若当前迭代次数k大于最大迭代次数,则终止多目标粒子群优化算法,输出最优解集,否则k=k+1并转步骤(6)。 通过案例研究希望达到的两个目的是:①以ZL水泥企业再制造为例,验证MMOPSO算法在多目标再制造物流网络优化中应用的有效性;②将MMOPSO算法与CNSGA-Ⅱ性能进行比较,验证MMOPSO算法在多目标优化中的优越性。 为验证MMOPSO算法在企业的再制造物流网络优化应用过程中的有效性,文中结合具体ZL水泥企业的再制造实践背景,求解多目标企业的再制造物流网络优化最优解结构。 3.1.1 背景描述 ZL水泥企业已实施掺加拆除建筑垃圾生产水泥熟料的再制造模式,2015年大约消纳15×104t建筑垃圾生产水泥熟料,节约煤粉7 409.5 t,减少CO2排放6×104t,在缓解资源匮乏的同时实现了节能减排。根据对ZL水泥企业再制造的实际调查,在某废旧桥梁拆迁点附近,存在2个备选第三方回收商。ZL水泥企业再制造正向供应链有3个备选原料供应商、3个备选再制造商、3个备选分销商和4个销售商,销售商需求分别为800 t,1 000 t,650 t,700 t。再制造商生产一单位水泥熟料需要1.5单位的掺合料,其中处理料的掺合比率为15%。调查分析ZL水泥企业再制造工艺流程,整理出该水泥企业再制造物流网络各节点的相关运营管理数据,如表1所示。ZL企业再制造各个节点运作过程中的直接碳排放因子通过美国能源信息机构(Energy Information Administration, EIA)分析报告和EcoInvent数据库估算得到,再制造商1~再制造商3回转窑燃煤及石灰石分解的直接碳排放因子分别为0.65,0.87,0.73 (tCO2/t)熟料。同时,耗电产生的间接碳排放因子采用华北区域消耗电力排放因子1.0416 tCO2/MWh。再制造商可根据实际情况选择不同等级碳减排技术,如表2所示。 ZL水泥企业将运输外包给第三方物流公司,并根据实际情况选择公路、铁路和水路3种运输方式,相关参数如表3所示。各备选节点之间的运输距离如表4和表5所示,其中括号中3个数字分别表示各备选节点之间采用公路、铁路和水路运输方式的运输距离。 表5 备选分销商到销售商的距离 km 3.1.2 优化结果 本文结合水泥企业再制造实际运营数据编写MMOPSO算法程序,寻求企业再制造物流网络优化结果。借鉴文献[6],设定碳税税率为每吨二氧化碳20元,Pareto最优解集中全局最优位置对应的最优总成本和碳排放量分别为3 670 723 元和1 786 t,该点对应的备选设施开设结构如表6所示。在开设的各个设施间,通过比较不同运输方式的成本、碳排放量和距离,得到各节点间的物流量如表7所示,这时再制造商1采用减排技术等级1、再制造商3采用减排技术等级2。 表7 已开设的各节点间采用不同运输的物流量分配 3.2.1 测试样本 为了衡量MMOPSO算法性能,文中将CNSGA-Ⅱ算法作为评价标准[20],分别计算小、中、大3种不同样本规模的再制造物流网络,比较两种算法获得的Pareto最优解集的差距,测试样本数据如表8所示。 3.2.2 性能指标 多目标企业再制造物流网络优化是一个NP-hard问题,其真实的Pareto前沿未知,因此借鉴文献[21],综合待比较算法求得的所有解,生成参照解集S*,来验证算法的有效性。文中采用以下3个性能指标评价MOPSO算法与CNSGA-Ⅱ算法的性能: (1)失误率(ER) 失误率即算法求得的非Pareto支配解的个数e与算法获取的解总数N的比率,采用式(32)计算得到[9]。ER值越小,解的质量越好, ER=e/N。 (32) (2)覆盖度(MS) (33) (3)运行时间(CT) 运行时间即算法获取最优解集所需的时间,单位为s,用来衡量算法的计算效率[9]。显然,运行时间越短,计算效率越高。 3.2.3 测试结果 不同问题规模下,MMOPSO算法与CNSGA-Ⅱ的Pareto最优解集如图2~图4所示,两种算法性能的比较结果如表9所示。 (1)在小规模问题中,MMOPSO算法和CNSGA-Ⅱ性能相当。由图2可见,在小规模问题下,MMOPSO算法和CNSGA-Ⅱ获得的Pareto最优解集完全相同。进一步通过3种性能指标定量比较二者性能,由表9可见,MMOPSO算法和CNSGA-Ⅱ解的覆盖率和失误率一致,而相对于CNSGA-Ⅱ,MMOPSO算法的计算时间较短。因此,对于小规模问题的求解,两种算法的搜索性能相当,且MMOPSO算法的运算效率较高。 (2)在中规模问题下,MMOPSO算法的性能优于CNSGA-Ⅱ。比较图3中不同算法的Pareto最优解集可知,CNSGA-Ⅱ获得的解劣于MMOPSO算法。进一步分析表9的性能指标可知,中规模问题下MMOPSO算法解的覆盖率高、失误率低、运行时间短,因此MMOPSO算法求解中规模问题的最优解集质量和分布性优于CNSGA-Ⅱ。 (3)在大规模问题中,MMOPSO算法的搜索性能明显优于CNSGA-Ⅱ,且CNSGA-Ⅱ在大规模问题求解过程中易陷入局部最优解,存在一定缺陷。由图4可知,在大规模问题下,MMOPSO算法Pareto最优解集的成本和碳排放明显低于CNSGA-Ⅱ。与此同时,CNSGA-Ⅱ算法求得的总成本在[5 931 682,6 436 394]元、碳排放在[2 998,3 208]t区间内陷入局部最优。相对而言,MMOPSO算法能在全局范围寻优,充分体现了MMOPSO算法在求解大规模问题上的优势。进一步分析表9的性能指标可知,虽然大规模问题下MMOPSO算法解的失误率略高,但其覆盖率和运行效率较高。 本文的首要任务是建立碳税政策下企业再制造物流网络总成本和碳排放优化的混合整数规划模型,随后采用MMOPSO算法寻求规划模型的Pareto最优解集。值得一提的是,文中设计有效约束处理机制,对MOPSO算法进行改进以解决约束优化问题,克服了传统多目标优化方法单点最优解的局限性。然后,为验证模型和算法的有效性,文中以ZL水泥企业再制造运营管理数据优化其再制造物流网络,确定该企业再制造物流网络的节点设施选址、运输方式的选择以及各节点之间的物流量分配,从而获得Pareto最优解集。最后,在小、中、大3种问题规模下分别比较MMOPSO算法与CNSGA-Ⅱ的性能,研究发现: (1)多目标水泥企业再制造物流网络存在最优结构,且最优组合解集中的总成本和碳排放量目标此消彼长,碳排放量的降低需要以提高成本目标为代价,这为水泥行业再制造决策提供了参考。 (2)当求解小规模问题时,采用MMOPSO算法与CNSGA-Ⅱ均能求得有效的Pareto最优解集,但CNSGA-Ⅱ的搜索效率略低。 (3)求解中、大规模问题时,MMOPSO算法获得的解质量和计算效率显著优于CNSGA-Ⅱ,另外在求解大规模NP-hard问题时,CNSGA-Ⅱ会陷入局部最优解,由此可见MMOPSO算法在求解多目标优化问题时的优越性。 企业再制造和物流运输过程中产生的废水、废气和噪音会对社区居民生活产生负面影响,这对本文研究提出了新的要求。因此,后续研究将从双目标混合整数规划模型延伸至3个或以上目标,在此基础上比较分析MMOPSO算法和CNSGA-Ⅱ在求解高维多目标问题时的性能。2.2 Pareto最优解集的存储
2.3 改进多目标粒子群优化算法的实现

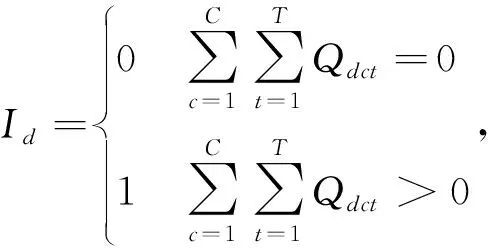




3 案例研究
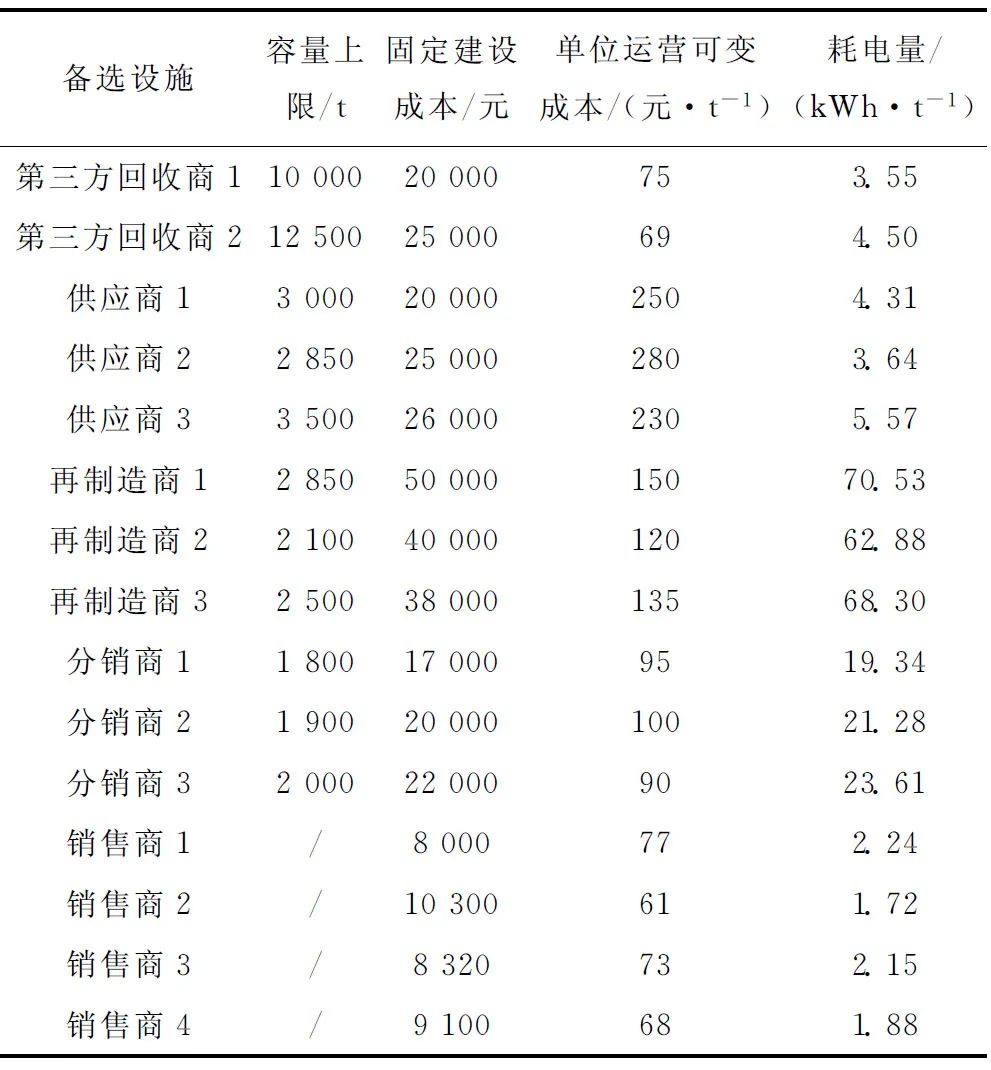
3.1 MMOPSO算法的实践应用






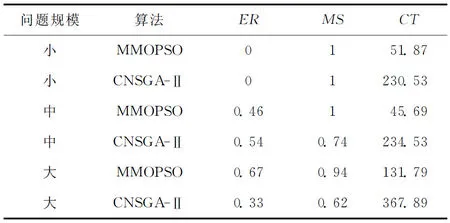
3.2 算法性能比较


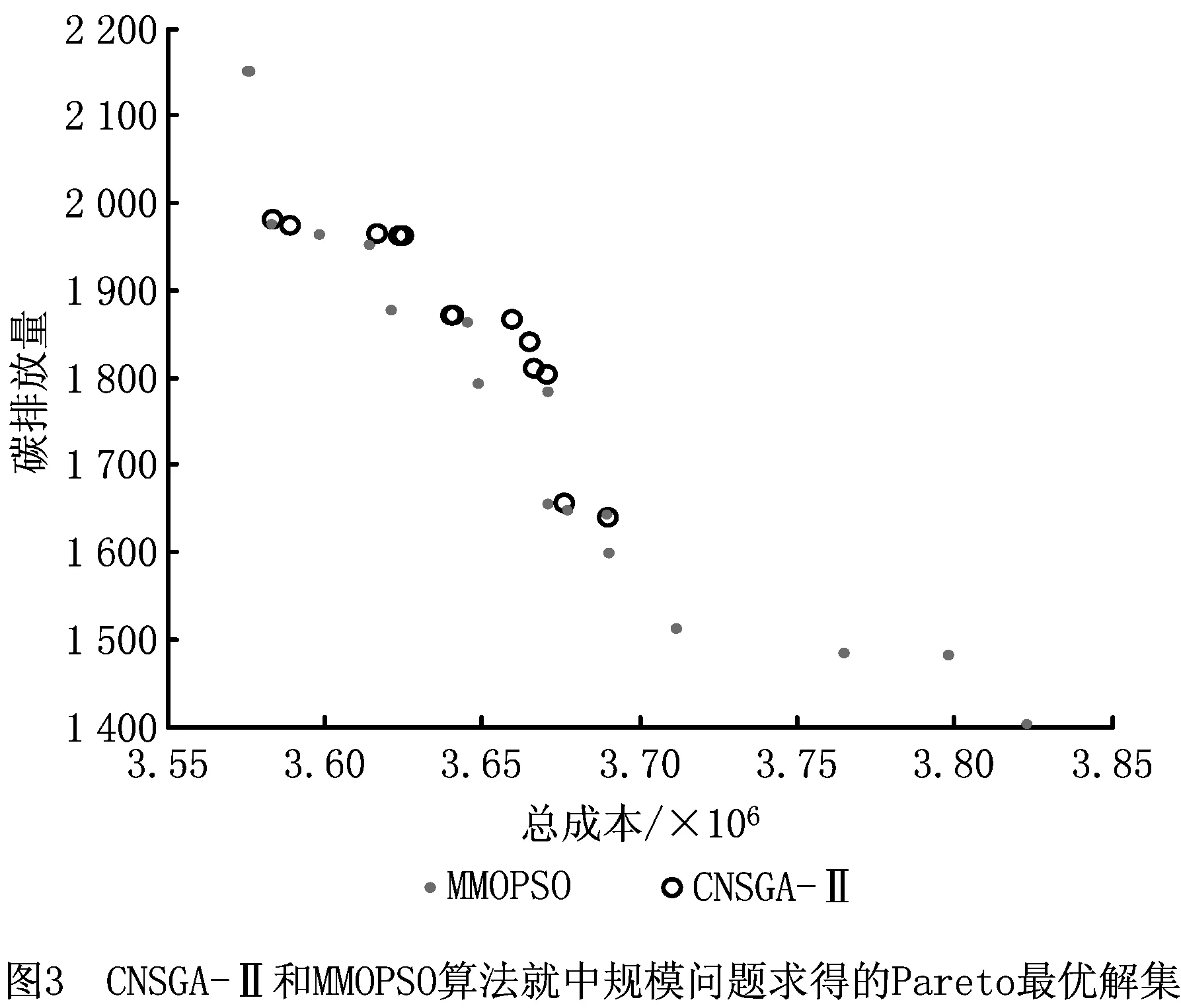

4 结束语
