基于员工学习行为的多目标柔性车间调度

曹 磊，叶春明，黄 霞,2

(1.上海理工大学 管理学院，上海 200093；2.江苏科技大学张家港校区 电信学院，江苏 张家港 215600)

0 引言

行为调度体现了企业、员工、顾客、环境、社会价值的多重统一，对提高企业效益、员工价值、顾客价值、资源利用率和社会效益具有重要的意义[1]。从制造、服务到供应链及产品研发的绝大多数运作中,人都是系统的重要组成部分，人类的行为可能会大大影响运作系统[2]。在实际生产中，人的行为具有多变性、复杂性，而大多数模型不考虑人的行为因素，忽略了人的素质禀赋、知识经验、认知状态等。近年来，一些生产制造领域的学者开始研究人的行为因素，构建了新的调度模型[3-5]。学习效应是实际制造系统中普遍存在的一种现象，研究学习效应有助于缩小理论研究与生产实践之间的差距，有助于生产型企业做出更为合理的决策。

Wright[6]通过研究航空制造业中人的行为对生产效率的影响，首次提出学习效应曲线理论，通过构建相应的函数对其进行量化，随后诸多学者对此进行了研究。Biskup最早提出了与工件加工位置有关的学习效应，并在文献[7]中对学习效应模型进行总结归纳。大多学者是在Biskup学习效应模型的基础上进行研究[8-11]。Lee等研究了一个双指标的单台机调度问题,目标是极小化一个包括完成时间和最大滞后的线性组合，给出一个分支定界算法和一个启发式算法帮助其寻找最优解和近似最优解[12]。然而，与工件加工位置有关的学习效应模型忽略了各工件之间加工时间的差异性，Kuo等[13]首先提出一种工件实际加工时间为前面所有工件基本加工时间之和的指数模型。基于位置的学习效应模型都存在一个共同的缺点，即当加工工件数量很大时,加工位置十分靠后的工件的实际处理时间会趋向于零。1957年，Dejong[14]提出一种学习效应模型，克服了Wright所提模型以及后续大量基于位置的学习效应模型的缺点，而且更加贴近现实生产环境，然而该学习模型在调度领域中却很少被研究。

如今，企业面临的经营环境日趋多样化和复杂化，顾客越来越重视产品的质量和服务，以往大批量连续生产的制造模式难以适应当前激烈的竞争环境。柔性作业车间调度问题(Flexible Job-shop Scheduling Problem, FJSP)完美体现了生产的柔性，工件的每一道工序可以在多台相同或不同的机器上加工。在FJSP中，决策者往往期望制造周期短、交货及时、机器负载均衡等，多目标柔性作业车间调度问题(Multi-Objective FJSP, MOFJSP)是一种更为实际的柔性生产作业模型。传统多目标优化方法有加权组合法、理想点法和极小极大法等，这些多目标优化方法或者是直接将多个目标合并为一个目标处理，或者是每次只考虑一个目标，其他目标通过不同方式(如排序等)作为约束进行优化。这些优化方法有一定局限性，例如权重系数一般需要由决策者事先给出；一些算法对Pareto最优前端的形状很敏感；往往一次仅能获得一个Pareto最优解[15]。近十几年来，通过模拟自然界中生物或物理过程而发展起来的元启发式算法越来越多地应用于研究MOFJSP，如遗传算法(Genetic Algorithm, GA)[16-18]、蚁群优化(Ant Colony Optimization, ACO)算法[19]、禁忌搜索(Tabu Search, TS)算法[20]、粒子群优化(Particle Swarm Optimization, PSO)算法[21]等。Kacem等是较早运用GA求解MOFJSP问题的学者，他们应用该方法同时优化最大完工时间、机器总负载和瓶颈机器负载3个目标[16-17]；张静等提出一种基于Pareto支配的混合PSO算法求解MOFJSP，3个目标与文献[16-17]一致，并通过求解基准案例验证了算法的有效性[21]；仲于江等[22]将小生境的概念引入PSO算法中，提出一种新型的混合算法，并通过实验验证了算法的有效性。从现有研究看，元启发式算法可有效求解MOFJSP，目标多是完工时间最大、机器总负载和瓶颈机器负载最小。为方便比较，本文所用的目标与文献[16]相同。

受杂草丛生现象启发，2006年Mehrabian提出一种新型的元启发式算法[23]——杂草优化(Invasive Weed Optimization, IWO) 算法，该算法原理简单、自适应性好，被广泛应用于函数寻优、天线队列设计、应急调度管理、DNA计算等。作为一种新兴算法，IWO算法已在诸多问题上得到了应用，但在生产调度中的应用较少，且基本没有应用于具有学习效应的多目标柔性调度研究。Dejong学习效应模型与Biskup模型相比更为一般化，模型中的“不可压缩因子”反映了加工环境中的人机配比情况。因此，本文考虑Dejong学习效应，构建了具有异质性学习效应的MOFJSP模型，并提出一种双段编码的变邻域杂草优化(Variable Neighbourhood Invasive Weed Optimization, VNIWO)算法求解该问题。

1 基于Dejong学习效应的调度问题

传统的面向制造的生产调度很少考虑操作者的参与体验，即便考虑，也多将人视为能够按照一定规则运作的完全理性人，忽略了人的素质禀赋、知识经验、认知状态、心理因素甚至社会环境的影响。而在基于学习效应的制造系统中，操作角色广泛参与于制造过程，他们不断学习、自我超越，是制造系统中最活跃的资源之一。

学习效应指生产者在长期生产过程中，通过不间断反复地做同一件事情，在一个合理的时间段内，由于知识的不断积累使得学习主体的经验得到增加，熟练程度得到提升，从而减少时间或成本的现象。受Wright在飞机制造业领域内学习效应研究的启发，Biskup[24]和Cheng等[25]开启了调度领域学习效应的研究。此后,大量学者致力于对生产调度领域中学习效应模型的研究，包括Koulamas等[26]、Biskup[7]、Lu等[27]、Cheng等[28]。以上研究大多基于工件位置，文献[7]对此类学习效应模型做了综述研究。基于位置的学习效应模型都存在一个共同的缺点，即当加工工件数量很大时，加工位置十分靠后的工件的实际处理时间会趋向于零。与Biskup模型相比，Dejong学习效应模型是一种更为一般化的模型[14]，即：

(1)

α=lgl/lg2。

(2)

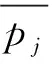
在生产系统中，员工的学习效果主要受初始能力、学习能力、任务难度和工作重复次数4个因素影响[29]。其中，任务难度和作业重复次数在很大程度上与作业本身有关，初始能力和学习能力主要与员工本身有关。为清晰表述员工的异质性，定义员工初始技能矩阵Pinitial和学习率L矩阵：

(3)

(4)

N位员工在正式上岗之前会有一定的岗前培训，之后被分配到N个不同工位上。不同员工接受新知识的能力略有不同，而且某些员工可能在以前的工作岗位上有类似的工作经验，这些都会在一定程度上影响员工的初始能力。初始能力矩阵Pinitial表征员工正式上岗前对每工位(本文指机器)的操作能力，学习矩阵L表征每位员工在不同工位的学习能力。考虑到员工的异质性，修正了Dejong学习效应模型：

(5)

αkm=lgLkm/lg 2。

(6)

修正模型除了考虑员工的初始技能水平，还兼顾员工后期的学习能力，然后将其应用到考虑员工技能异质性的柔性作业车间调度中。

2 基于学习行为的多目标柔性制造系统

为方便讨论，引入数学符号，如表1所示。FJSP比传统作业车间调度问题更加接近实际调度情况，其可用数学模型描述为：Jj∈{J1,J2,…,Jn}的所有工序被安排在m台机器上加工，同工件各工序间存在固定的加工顺序，每一道工序都有其特定的机器集合，且至少有一道工序的机器集合中的机器个数大于1。

注：数字符号含义仅适用于本章。

求解FJSP的关键是为工序分配适当的机器，并对每台机器上的工序进行排序，根据工序约束和机器约束计算出每道工序的开始时间和结束时间，从而求得制造系统的某个或某些指标的最优或近似最优解。一般FJSP需满足如下约束：

i=1,2,3,…,m，j=1,2,3,…,n，

h=1,2,3,…,hj；

(7)

cjh≤sj(h+1)，j=1,2,3,…,n，

h=1,2,3,…,hj-1；

(8)

cjhj≤Cmax，j=1,2,3,…,n；

(9)

j=1,2,…,n，k=1,2,3,…,n，h=1,2,3,…,hj，

l=1,2,3,…,hk，i=1,2,3,…,m；

(10)

cjh≤sj(h+1)+L(1-yiklj(h+1))，

j=1,2,…,n，k=1,2,3,…,n，h=1,2,3,…,

hj-1，l=1,2,3,…,hk，i=1,2,3,…,m；

(11)

(12)

l=1,2,3,…,hk，i=1,2,3,…,m；

(13)

j=1,2,3,…,n，h=1,2,3,…,hk；

(14)

sjh≥0,cjh≥0，j=1,2,…,n，h=1,2,3,…,hj。

(15)

其中：rih表示当前工序在机器i上的加工顺序；式(7)和式(8)表示工序间存在先后约束；式(9)表示在给定的调度方案下，每一工件的完工时间存在上界Cmax；式(10)和式(11)表示同一时刻同一台机器只能加工一道工序；式(12)表示机器约束，即同一时刻同一道工序只能且仅能被一台机器加工；式(13)和式(14)表示每一台机器存在循环操作；式(15)规定了工序的开始和结束时间均非负。

在实际FJSP生产环境中，管理者的决策往往涉及诸多目标，这些目标有时互相冲突，管理者根据生产需要选取几个目标进行优化，并根据自己的偏好在Pareto解集中按照一定的规则选择某一调度方案。本文基于车间层面选择3个目标进行优化，即最小化最大完工时间、最小化机器总负载、最小化瓶颈机器负载。3个目标定义如下：

(16)

(17)

(18)

3 算法设计

3.1 杂草算法的优化机理

杂草是指非栽培的野生植物或对人类无用的植物。在自然环境下，杂草具有超强的环境适应能力和繁殖能力。由于限定区域内资源的稀缺性，适应性强的杂草有较大几率存活并产生子代，从而使区域内杂草群体的适应性得到提升。IWO算法中存在如下对应关系:杂草个体—可行解、杂草种群—可行解集、空间扩张—位置更新、资源限制条件—杂草种群规模限制。从以上分析看，IWO算法体现了大自然中种内竞争、优胜劣汰的生态现象。优势杂草个体会产生更多子代，如式(19)所示；迭代后期，种内竞争加剧，杂草扩张能力逐渐减弱，如式(20)所示。

(19)

式中：fbest和fworst分别表示当前杂草种群中最优杂草和最差杂草的适应度；fitnessi表示第i个体的适应度；smax和smin分别表示杂草个体产生种子个数的上界和下界。

新生种子在父代周围繁殖，繁殖半径与迭代次数有关，如式(20)所示。种子在每一维度上的实际步长服从均值为0、标准差为σ的正态分布。

(20)

式中：iter为当前迭代次数，itermax为最大迭代次数，σinit和σfinal分别为繁殖半径初始值和终止值，n为非线性调和因子。可见，杂草种群的繁殖半径随迭代的进行呈逐渐减少的趋势，从而使算法在前期具有较强的全局搜索能力。随着σ的逐步减小，子代杂草围绕父代杂草进行局部搜索。

IWO算法使用不固定规模的种群μ(即μ≠λ)，但有最大杂草规模限定，父代种群λ和子代种群μ中的λ+μ个体中选择适应度值较优的个体作为新一代种群Pg，这种选择方式称为(λ+μ)-ES演化策略，可描述为

γt=[μ≠λ,(μ+λ),记录并更新Pg]。

(21)

算法流程图如图1所示。

3.2 杂草个体编码

编码策略是解决调度问题的基础和关键。根据第1章和第2章描述，基于学习行为的MOFJSP需要解决人员指派、工序排序和机器选择3个子问题。对于传统的FJSP，学者们一般采用文献[22]中的二段式编码方式解决工序排序与机器调度问题。本文采用连续二段式编码方式对杂草个体进行编码，前段表示工序排序，后段表示人员指派，机器选择采用启发式方法。

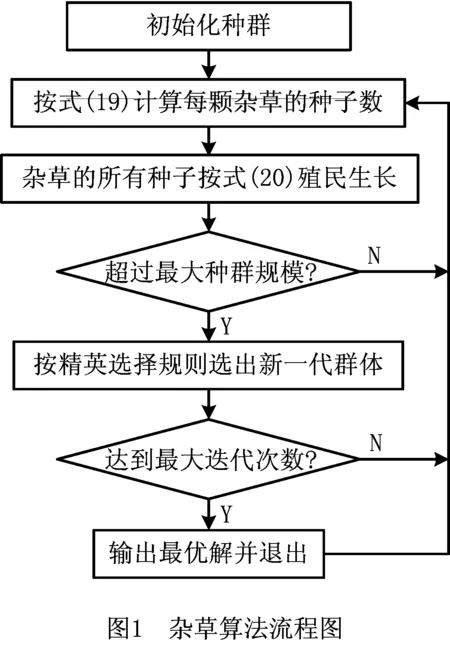
从IWO算法的优化机理可以看出，基本IWO算法可以直接用来解决连续优化问题，而要求解本文模型，需要提出一种有效的编码方案，使杂草个体可以解释为一可行的调度方案。随机键编码是一种较为有效的编码方式，它可以实现连续空间到离散空间的映射[30]。以一2工件3机器完全FJSP为例(如表2),杂草个体由前后两段构成，前段编码长度为工序总数，后段编码长度为员工总数，其前段x1=[0.814 7,0.901 8,0.127 0,0.913 4,0.639 4]，后段x2=[1.2,2.8,1.8]。

3.2.1 工序解码与机器选择

工序的解码过程如图2所示，按照位置分量从大到小排列工件号(分量值相同时近左优先)。为保证排序的合法性，同类工件号的排列顺序表示工序的先后顺序。

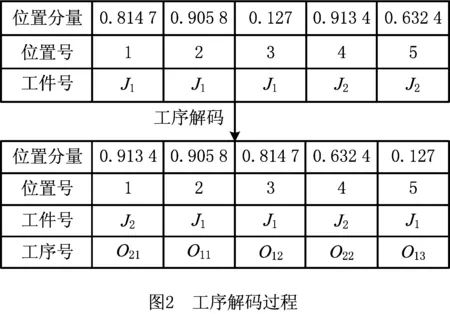
对每道工序采用贪婪策略选择机器。设Mjh为工序Ojh可选的加工机器集合，集合中机器Mi已完成li道工序的加工任务，完工时间为m_endili,工序Oj(h-1)的完工时间为j_endj(h-1)，则工序Ojh在机器Mi上的预完工时间Cijh=max(m_endili,j_endj(h-1))+tijh；在机器集合Mjh中，选择使Cijh最小的机器Mi′作为Ojh的加工机器，则最终Ojh的完工时间

(22)

3.2.2 员工指派

对于后段向量，基于ROV(ranked order value)随机键编码方式，使个体的连续位置矢量与员工所处的机器位置一一对应。与3.2.1节类似，根据每个员工对应的位置分量值，依次挑选分量大的员工，将其安排到未有员工操作的机器号最小的机器上，当位置分量相同时，优先挑选员工号小的员工。图3所示为员工指派的解码过程。

3.3 变邻域搜索策略

邻域是优化领域中的一个重要概念，它定义了基于当前解或解集的搜索方向和范围。对于一般的连续优化问题，邻域可视为以一点为中心的球区域。组合优化问题不再适用传统的距离概念，需要定义新的邻域结构。变邻域搜索算法(Variable Neighborhood Search, VNS)是一种基于局部搜索算法提出的一种启发式算法，该方法已被学者们用于求解诸多组合优化问题。邻域结构的设计是VNS算法的关键，本文采用以下3种邻域结构：

(1)N1(逆序) 在可行工序序列中任意选择两个位置，将其中间的工序逆序排列，并按照工序约束修正非法解。

(2)N2(交换) 选择两个工序位置对调工序，并按照工序约束修正非法解。

(3)N3(最小加工时间) 选择任意一个工序，在其可选机器集合中选择加工当前工序时间最短的机器。

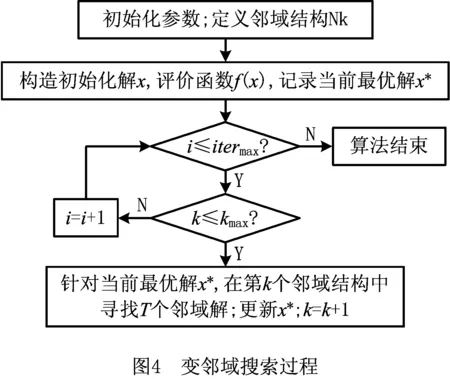
VNS算法的基本思想是在给定的邻域结构中不断尝试不同的搜索策略，基于“贪婪接受”的思想求得局部最优解，并重复以上过程，经过若干代迭代输出结果。VNS算法流程图如图4所示。

3.4 非支配排序和拥挤距离排序

非支配排序[31]根据个体的非劣解水平对种群进行分层。该方法通过计算种群P中每个个体i的两个参数Si和ni划分出非支配前沿Fi(i=1,2,…,k,k为非支配前沿数)。其中Si为被个体i所支配的解个体的集合,ni为在种群中支配个体i的解个体的数量。非支配排序算法的复杂度为O(mN2),m为目标函数个数，N为种群大小，该算法的具体步骤如下：

步骤1k=1，找到种群中ni=0的个体，将其存入当前集合Fk。

步骤2对于当前集合Fk的每个j，考察其所支配的个体集Sj，并将集合Sj中的每个个体q的nq值减1，若nq=0，则将个体k分入下一层非支配前沿Fk+1。

步骤3令k=k+1，如果Fk非空，则转步骤2；否则，返回前沿F1,…,Fk并结束非支配排序。

多目标优化的目的在于发现一组解而非单个解方案，在保证解质量的前提下尽可能找到一组均匀分布的非劣解集。为描述群体的分布情况，利用拥挤距离刻画个体间的聚集程度。一般情况下，拥挤距离大的个体的聚集密度小。设I[i]distance表示种群I中第i个个体的拥挤距离，I[i].k表示第i个个体在子目标k上的函数值，当有m个子目标函数时，个体i的拥挤距离[31]

(23)

Crowding-distance(I)

{ l=|I|;

initial所有个体I[i]distance=0

for each m∈M

{I=sort(I，m)

I[1]distance=I[l]distance=∞

i=0

while(1≤i≤l)

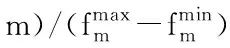
i=i+1

}

}

其中，sort(I,m)是按第m个目标函数值对群体I排序的函数。通过计算非支配排序和拥挤距离，群体中所有个体都有排序号和拥挤距离两个特征向量。比较两个个体时，如果非劣层级不同，则取层级高的个体；如果两个个体在同一层级，则取拥挤距离大(聚集密度小)的个体。用I[i]rank表示i个体的排序，得到i和j的偏序关系≻n：

i≻nj=

(24)

3.5 灰熵关联适应度分配策略

在多目标优化算法中有多种适应度值分配策略，如基于Pareto优先关系排序的适应度值分配策略、基于随机权重求和的适应度值分配策略、选择性权重的适应度值分配策略等。熵是一种度量微观分布均匀性的方法，其在热力学中表示系统的混乱状态，而在生态学中表示物种的多样性。近年来，学者们尝试将熵与元启发式算法融合来解决优化问题[32-34]，本文借助熵值权重的思想，提出基于灰熵关联的适应度值分配策略，具体步骤如下：

步骤1分别对单目标进行寻优，求出各子目标函数的最优值fm(0)(m=1,…,M)，组合为理想解的目标函数值序列Y0={f1(0),f2(0),…,fM(0)}，M为目标个数。另外，对种群中的可行解xi，分别计算其子目标函数值fm(i),组成序列Yi={f0(i),f1(i),…,fM(i)}。其中：m=1,…,M，i=1,2,…,N。

步骤2对理想解和可行解的子目标函数值序列作无量纲化处理：

(25)

步骤3求灰关联系数

(26)

式中ρ为分辨系数，一般取ρ=0.5。

步骤4求可行解各子目标的比重

(27)

步骤5求可行解各子目标的信息熵

em(i)=-pm(i)lnpm(i)。

(28)

步骤6求可行解各目标的熵值权重

(29)

步骤7求可行解的灰熵关联度

(30)

3.6 外部档案更新

本文杂草种群中存在外部档案子群(ES)和繁殖子群(pop)两个子群。其中，外部档案存储了非劣解集，可被繁殖子群更新。总种群规模为N，外部档案子群规模为N1，繁殖子群规模为N2。外部档案子群记录非支配子集，繁殖子群记录非支配前沿Fi(i=1,2,…,k,k为非支配前沿数)。第一代外部档案取自繁殖子群中的F1，若非劣解个数大于N1，则取前N1个个体，否则取F1的所有个体。外部档案生成后，可用繁殖子群(pop)对外部档案子群ES进行更新，伪代码如下：

Update_ES(pop)

{ Q=pop;

while(Q不为空集)

{

x∈Q,令Q=Q-{x};

x is nondominated;

for each y∈ES

{

if(x dominated y)then

ES=ES-{y};

else if(y dominated x)then

x is nondominated=false;

}

if(x is nondominated)then

ES=ES∪{x};

}

if |ES|≥N2then

crowding-distance(ES) select 前N2个

}

3.7 算法流程

综上所述，求解MOFJSP的VNIWO算法流程归结如下：

步骤1设置参数,包括初始杂草个数G、最大杂草个数P、问题的维数D、目标个数M、初始标准差σinit和最终标准差σfinal、扩张区间大小、最大最小种子数(smax和smin)、最大迭代次数、变邻域搜索次数VN、外部档案规模N1。

步骤2按照3.2节的编码规则初始化杂草群体，计算3个子目标的适应度值，并按照3.6节计算出灰熵关联度，作为杂草个体的适应度值。

步骤3根据3.6节生成外部档案。

步骤4运用IWO算法进行迭代优化，按式(19)计算杂草个体的子代个数，杂草的种子按式(20)以随机步长在一定范围内进行空间扩张生长出新杂草，并将新生成的杂草加入杂草群体。计算新生杂草的适应度值，取排名前10%的精英杂草进行变邻域搜索。将变邻域搜索得到的优良个体按3.6节更新外部档案子群ES，杂草群体按3.4节方法对新杂草群体进行非支配排序和拥挤距离排序。

步骤5判断杂草群体是否达到预设的最大种群规模，是则按精英选择策略选出下一代繁殖杂草群体，并用该群体按3.6节更新外部档案子群ES。

步骤6判断是否达到终止条件，是则输出调度方案和目标函数值并终止算法，否则转步骤4。

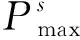
O(M(P+Psmax)·log(P+Psmax))

=O(MP(1+smax)·(logP+log(1+smax)))

≈O(M(1+smax)PlogP)。

(31)

4 仿真实验

本文算法采用MATLAB 2010b编程语言实现，运行环境为：处理器主频2.1 GHz，内存2 GB、Windows7操作系统。VNIWO算法参数设置如下：最小杂草个数为10、最大杂草个数为15、非线性因子n=4、最小最大种子分别为1和3、初始和终止步长分别为0.1和0.001，邻域搜索次数为20，最大迭代次数为100。

4.1 算法性能测试

为了验证本文所提VNIWO算法的性能，求解文献[17]中8×8,10×10,15×10 3个不同规模的基准问题，并与Kacem的局部搜索受控遗传算法(Approach by Localization and Controlled Genetic Algorithm, AL+CGA)[16]、Xia的粒子群模拟退火混合算法PSO+SA[35]、Zhang的粒子群禁忌搜索混合算法PSO+TS[36]、Wang的多目标遗传算法(Multi-Objective Genetic Algorithm, MOGA)[37]对比，实验结果如表3所示。针对基准案例中一部分柔性案例(8×8)和完全柔性案例(15×10)，绘制Pareto解集中一个解的甘特图，如图5和图6所示。

表3 Kacem基准问题对比实验

从实验结果可以看出，VNIWO求解8×8问题所得非劣解集中解的个数更多，而且分布性较好；求解10×10问题时非劣解集中解的个数有一定优势，非劣解集解的个数少于MOGA而多于AL+CGA，PSO+SA，PSO+TS；求解15×10问题得到的非劣解集支配AL+CGA，PSO+SA，PSO+TS和MOGA求得的非劣解集数目均为1，但与MOGA相比，VNIWO在支配性能指标上不占优势。综上，VNIWO可有效求得8×8问题的可行解，而且解的质量也有一定优势。

4.2 案例分析

以8×8问题为例，分析具有异质性员工学习效应的FJSP。车间有员工8名，且均为新员工。经过技能考核，员工的初始技能水平和学习能力情况如表4所示。括号外的数值为初始能力(与Pinitial中的相应值对应)，初始能力值可解释为员工初始操作时间与标准操作工时(与原问题机器标准加工时间对应)的比值，值越小表示员工对某一机器操作越娴熟;括号内的数值为员工学习率，表征员工对技能的领悟能力，根据第1章描述，学习率越小，领悟能力越强。

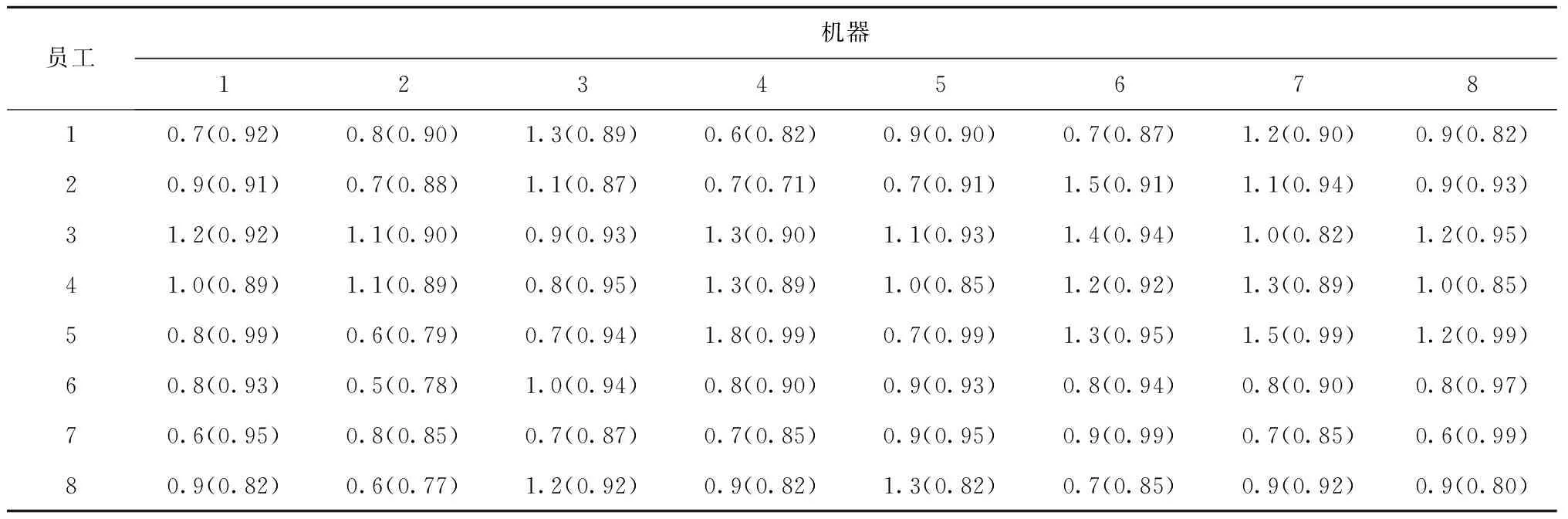
表4 员工技能水平

在Dejong学习效应模型中，F为不可压缩因子，F=0，1分别表示一个完全手工操作生产和完全由机器控制生产的加工环境。从实际角度看，一个合适的F值的设定取决于具体的加工任务。因此，研究Dejong学习效应模型中的F值，可以发现学习效应对不同制造系统的影响，缩小理论研究与实际生产间的差距，有助于决策者做出合理的决策。针对不同的F值，用VNIWO算法求解案例，独立运行5次后合并非劣解集(部分)，统计结果如表5所示。图7所示为完全手工环境下，非劣解集中的一个可行解甘特图，员工指派方案如表6所示。敏感性分析指定量描述分析模型因素变量对优化目标函数值的重要性程度，一般用敏感系数表示为

(32)

式中：SfA表示模型目标值f对因素变量A的敏感程度；ΔA/A表示因素变量的变化率；Δf/f表示因素变量变化ΔA时引起模型目标值的变化率。在此分别分析3个子目标函数值对M的敏感程度，3个子目标函数值取Pareto集合中目标分量的平均值，计算结果如表7所示。

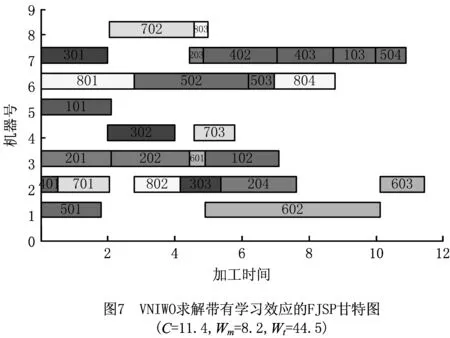
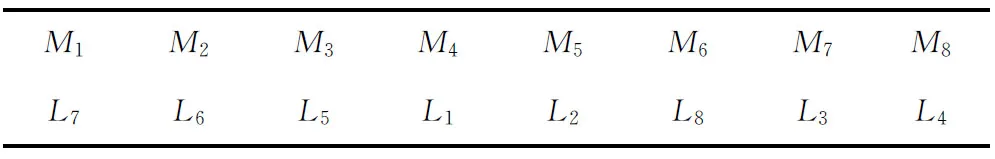
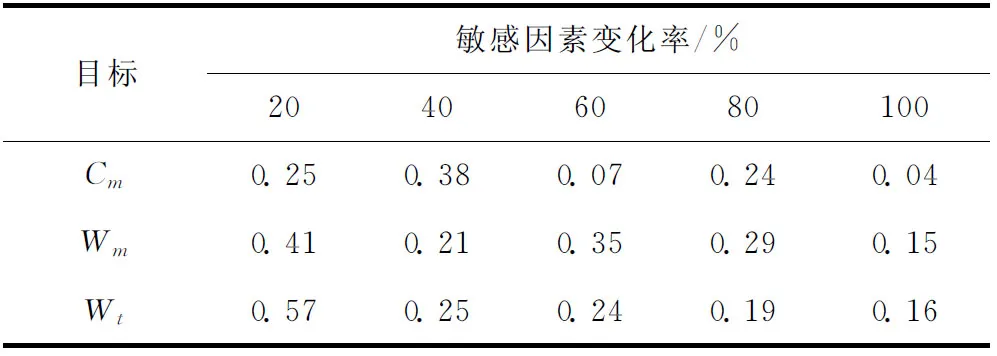
实验数据表明，本文所提算法对不同M值的柔性作业车间均可给出较为满意的非劣解集，3个目标函数值对M值的敏感度略有不同。从表6可以看出，3个子目标函数值变化与F值的变化成明显的正相关性，且幅度有减小的趋势。仅在敏感因素F变化80%时，总机器负载的变化率同时小于最大完工时间和瓶颈机器负载两个子目标的变化率。在本文案例中，异质性多技能员工的存在，使得制造系统更具有柔性和学习性，知识和经验的积累使总机器负载减小的程度比较明显。关键工序链短和瓶颈机器上的工序数目少，学习效应积累程度不大，原因可能是最大完工时间和瓶颈机器负载两个目标对M值变化较不敏感。

5 结束语

本文研究了一类带有学习效应的MOFJSP，提出VNIWO算法对其进行求解。采用随机键编码的方式将杂草个体映射为一可行的调度方案，解决了工序排序、机器选择和人员指派等问题。针对多目标问题的难解性，采用非支配排序和拥挤距离排序对杂草群体进行精英筛选和更新，给每一个杂草个体赋予一灰熵关联适应度值，以方便其产生子代个体。在几个存在异质性员工学习效应的柔性作业车间调度系统中，用灵敏度分析考察子目标函数值对F值变化的灵敏度。案例分析表明，制造系统中的学习效应对与加工时间有关的目标函数值有一定影响；不同子目标对F变化的灵敏度是有差异的，总机器负载的灵敏度较大。

本文采用的案例是连续作业系统，并未考虑休假、停机等干扰影响，因此设计有效算法，构建更为精细的行为调度模型，并将其运用到生产运营管理中，将是今后研究的重点。