压缩感知框架下的共振解调故障诊断方法
2018-09-08易灿灿
王 珂 吕 勇 易灿灿
1.武汉科技大学冶金装备及其控制教育部重点实验室,武汉,430081
2.武汉科技大学机械传动与制造工程湖北省重点实验室,武汉,430081
0 引言
风力发电机一般安装在环境恶劣的偏远地区,工作时间长、强度高,容易发生故障。滚动轴承是风电机组中重要的支承元件,特别是主轴、齿轮箱和发电机中的轴承,一旦发生故障且未在故障早期及时发现,不仅可能引发新的故障,还会使设备损坏,造成巨大的经济损失,因此,基于风力发电机的早期故障诊断研究对保障其安全运行意义重大[1⁃2]。
滚动轴承是风力发电机组中最易损坏的零件之一,当其转子承受不平衡、不对中、松动或点蚀等引起的动载荷时,即使在故障早期,也会产生冲击振动[3⁃4]。一般的频谱分析很难检测出这种微弱的冲击振动,故常用共振解调技术来解决这一问题。共振解调技术[5⁃6]是对低频冲击所激起的高频共振波进行带通滤波和包络检波,获得一个被放大、展宽且能反映故障信息的低频包络信号,通过对此包络信号进行频谱分析,来判断故障的程度和类型,适用于轴承的早期故障诊断。
故障振动信号中的噪声对共振解调的效果影响很大,所以对信号进行有效去噪显得尤为重要。CANDES等[7]于2004年提出的压缩感知(com⁃pressive sensing,CS)[8]理论备受关注,因其能够充分利用信号的稀疏性来压缩信号,常被用于信号去噪[9]。CS理论的核心内容是假设信号在某个变换域是稀疏的,即是可压缩的,可以通过某个线性测量矩阵将高维稀疏信号投影于低维空间,然后提取极少量的投影测量值来对信号进行重构,最后得到一个近似度很高的重构信号。由于噪声一般是随机且没有结构的,难以进行稀疏表示,通过设置合适的稀疏度,可以用少数几个原子稀疏表示信号故障成分,忽略噪声或其他无关信息,从而直接提取故障特征[10]。常用的CS重构算法[11]有正交匹配追踪(orthogonal m atching pursuit,OMP)算法[12]、压缩采样匹配追踪(com pressive sam pling M P,CoSaMP)算 法[13]和 子 空 间 追 踪(subspace pursuit,SP)算法[14]等。其中,OM P算法重构信号的成功概率不及CoSaM P和SP算法,且所需的迭代次数也相对较多[11]。以上算法的重构效果均依赖于稀疏度的准确估计。唐刚等[15]利用信号故障成分在傅里叶域的稀疏度已知这一特点,采用CoSaMP算法对实测信号进行不完全重构,成功提取出反映故障特征的共振谐波,但是其采用的实验数据是相对较“干净”的轴承故障信号,并没有对含噪较多的轴承故障信号进行进一步的去噪研究。另外,SP算法每次迭代选择的原子是CoSaMP算法的一半,计算效率相对更高。综上,本文采用傅里叶变换基来稀疏表示反映故障信息的包络信号,并利用压缩感知子空间追踪(CS_SP)算法对其进行重构去噪,获取风力机滚动轴承的故障特征频率,从而进行故障诊断。
1 压缩感知和共振解调理论
1.1 压缩感知理论与子空间追踪算法
压缩感知的处理流程主要涉及三方面:一是稀疏表示;二是观测矩阵的设计;三是信号重构。压缩感知的首要步骤是对信号进行稀疏表示,信号的稀疏表达效果依赖于稀疏度的设置。信号的稀疏度指信号的稀疏表示系数中非零元素的个数。一般情况下,信号的稀疏度是未知的。研究发现[16],在傅里叶域,每个谐波成分对应的频率特性为两条谱线,即故障引起的共振谐波分量需要用两个原子来线性表达,也就是说,信号的故障信息分量在傅里叶域的稀疏度K=2。若可以只对信号中的故障成分进行重构,就解决了压缩感知重构算法中稀疏度难以确定的问题。
假设一个由稀疏变换基Ψ表示的信号x∈RN×1,通过设计一个与Ψ最大不相干的测量矩阵Φ∈RM×N(M≪N)和线性投影算法,实现信号x的同步压缩,即
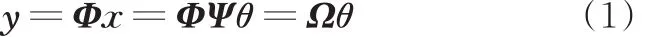
式中,y∈RM×1为压缩信号;θ∈RN×1为信号x的稀疏表示系数;Ω∈RM×N为传感矩阵。
再通过压缩感知重构算法求解稀疏系数θ,本文选取的压缩感知重构算法为SP算法。该算法为了提高重构精度,不同于OMP算法每次迭代只选取一个原子,而是借用回溯的思想,在每步迭代过程中从原子库里选择多个相关原子,同时又从这些选择的原子中依照某种限制条件剔除部分不相关原子。相比于传统的OMP算法,SP算法不仅具有更高的重构精度,还具有更小的运算复杂性和更快的运算速度。
SP算法具体计算步骤如下:
(1)初始化残差r=y,迭代次数Iter=1,索引集Λ=∅,Λ1=∅;
(2)由u=|〈r,Ω〉|,计算残差和观测矩阵中各列的内积u,然后从中找出最大的K个值,并将其对应的观测矩阵中各列的索引值放入Λ1,其中:
u={un|un=|〈r,Ωn〉|,n=1,2,···,N} (2)式中,Ωn表示传感矩阵中的各列;N为传感矩阵的列数。
(3)扩充索引值Λ=Λ⋃Λ1;
(4)由y= Ωθ,求θ的最小二乘解θ^,然后从中寻找出最大的K个值,并将其对应的观测矩阵中的各列放入支撑集ΩA,其中:
θ^=argm in‖ ‖y-Ωθ =(ΩTΩ )-1ΩTy (3)
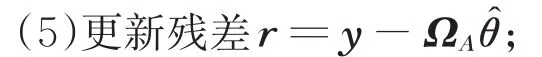
(6)若残差r=0或Iter=K,则停止迭代,输出;否则,Iter← Iter+1,返回到步骤(2),继续迭代。
(7)最后可得到重构信号:

1.2 共振解调技术
风力机滚动轴承的内圈、外圈或滚动体存在不规则损伤时,轴承转动会引起冲击振动。但故障早期的冲击振动强度一般较弱,频谱图中常会出现冲击振动频率被基础振动频率所淹没的现象,所以只通过信号的频谱分析难以识别轴承的早期故障,需利用共振解调法来提取埋藏于基础振动信息中的故障冲击信息[17]。
轴承故障产生的冲击振动是一个宽带信号,其中必有一部分能量落在加速度传感器的谐振范围内,即加速度计的谐振频率在冲击振动的频率带宽内,因而会引起加速度传感器的共振[18]。共振解调法是利用加速度传感器的共振特性,将故障冲击引起的衰减振动放大,再通过以共振频率为中心频率的带通滤波器滤波,将信号的故障特征信息分离出来,然后经包络检波,提取反映故障信号的低频包络信号,最后通过频谱分析获得故障特征频率,从而进行故障诊断。
共振解调技术对信号进行故障诊断的效果受信号中的噪声和无关信息的影响较大,所以对信号的去噪和对滤波频率范围的适当设置是故障诊断成功的关键。
2 压缩感知框架下的共振解调故障诊断方法
本文的技术路线见图1。首先,线路①中通过快速傅里叶变换(fast Fourier transform,FFT)获取风力机信号的频谱图,依靠信号的频谱分析自动识别信号的高频共振频带[19];接着通过线路②,以获得的共振频带为滤波频率范围对信号进行滤波处理,来滤除部分噪声和无关成分;然后通过包络检波获取对应故障信息的包络信号,并使用傅里叶变换基和CS_SP算法对包络信号进行不完全重构;最后依靠重构信号的频谱分析来提取信号的故障特征频率。通常,由故障产生的共振谐波信号在傅里叶域的稀疏度是已知的,即K=2[16],在使用傅里叶变换基和CS_SP算法对故障信号进行重构时,由于包络信号中反映信号故障特征的低频信号的能量远大于滤波信号中的噪声能量,最先重构的必定是信号故障成分。设置稀疏度K=2,直接重构出反映故障特征的信号成分,即可忽略噪声和无关信息的影响。
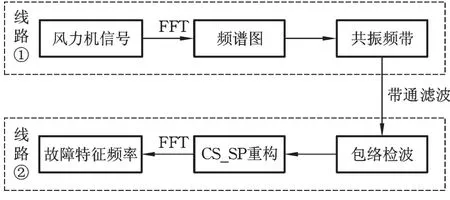
图1 压缩感知框架下的共振解调故障诊断方法技术路线Fig.1 Flow chart of resonance dem odulation based on com p ressive sensing and its app lication in fau lt d iagnose
3 仿真实验
为了验证所提算法的有效性,用以下仿真信号进行实验:
x(t)=x1(t)+x2(t)+xn(t) (5)
x1(t)=(1+cos(2πft))cos(2πf1t)x2(t)=cos(2πf4t)+0.6cos(2πf5t)
x1(t)对应调制频率为f=20 Hz的调幅信号,其中载频f1=200 Hz,上边频f2=220 Hz,下边频f3=180 Hz;x2(t)对应频率为f4=50 Hz和f5=70 Hz的谐波信号;xn(t)为标准差为3的高斯白噪声。信号x(t)的采样频率为1 000 Hz,采样时间为2 s,原信号的频谱图和包络谱图分别见图2、图3。
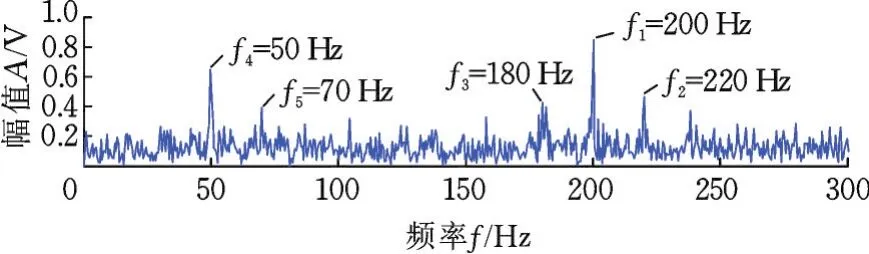
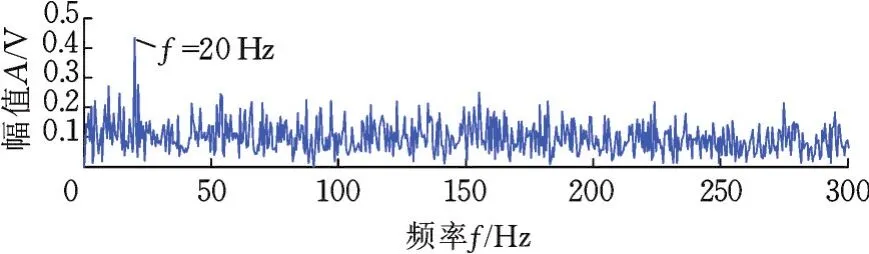
图3 原仿真信号的包络谱图Fig.3 Envelope spectrum of the original signals
本实验的目的是抑制谐波信号和高斯白噪声,提取出混合信号中的调制频率20 Hz。由图2的频谱图无法提取出20 Hz的调制频率。通过图3的包络谱图也只能从较大的底噪声频率中勉强识别出f=20 Hz的调制频率,结果不具有说服性。若采用本文提出的方法,先通过对原信号的频谱分析,识别出调幅信号频率范围在180~220 Hz之间,将共振解调过程中的滤波频率范围设置为150~250 Hz,再依据技术路线中的路线②获取重构信号的包络谱,如图4所示,可提取出明显的f=20 Hz的调制频率,从而验证了本文方法的有效性。
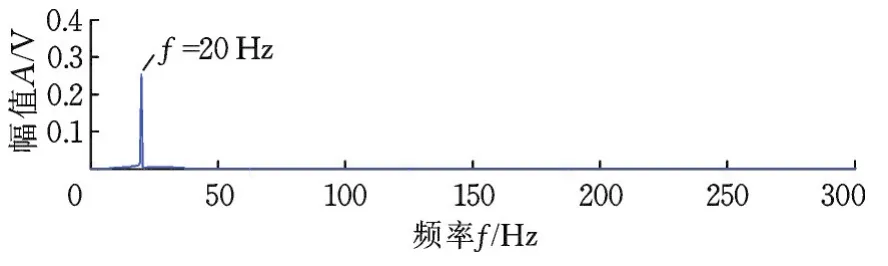
图4 重构的仿真信号包络谱图Fig.4 Envelope spectrum of reconstructed signals
4 压缩感知和共振解调技术在风力机轴承故障诊断中的应用
本文采用的风力机滚动轴承故障数据来源于某公司1.5 MW直驱永磁风力发电机。该风力发电机组主要部件及传感器测点布置如图5所示,其中,1H为主轴承水平方向、1V为主轴承垂直方向、1A为主轴承轴向方向、2V为转动轴承垂直振动、3H为定子水平振动、4H为转子水平运动、4A为转子轴向振动。
选取风力机后轴承水平振动(1H)信号作为处理对象,首先通过FFT变换获取信号的频谱图,结果见图6。由图6可知,原风力机信号频谱图中凸显出了两个频率,f1=166.9 Hz和f2=330.5 Hz。通过查阅所研究风力机的电气特征频率(表1)和机械特征频率(表2)可知,上述频率分别对应表1第4组中齿槽基频的二倍频和四倍频,并非故障频率。另外,在频率f3=230.5 Hz和f4=267.3 Hz之间,频谱图中出现了明显的峰值间隔相近的波峰,由此可判断此频段在共振频带内,则确定共振解调的滤波频率范围为229~268 Hz。

图5 直驱永磁风力发电机组结构及传感器测点布置Fig.5 Structure of d irect d rive perm anentm agnetw ind turbine and arrangem en t of sensor m easuring points
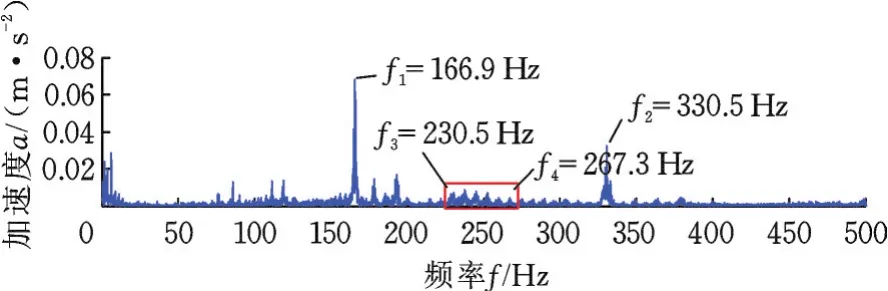
图6 原风力机信号频谱图Fig.6 Frequency spectrum of originalw ind tu rbine signal

表1 风力机电气特征频率Tab.1 Electrical characteristics frequency of w ind turbine

表2 风力机机械特征频率(额定转速下)Tab.2 M echanical characteristic frequency ofw ind turbine(under rated speed)
利用获得的共振解调滤波频率范围对信号进行滤波处理,再对滤波信号进行包络检波,并利用CS_SP算法以2为稀疏度对包络信号进行重构去噪,获得其包络频谱,从而提取信号故障特征频率。重构结果见图7。

由图7可提取频率f=7.422 Hz,通过查阅表2可发现,它与第5组中风力机后轴承的内圈间隔频率一致,由此可确定f=7.422 Hz为风力机后轴承内圈的故障特征频率,即可判断风力机后轴承的内圈发生了故障,这与现场的实际情况一致,同时也验证了本文提出方法的有效性。
5 结论
(1)针对噪声和其他无关信息影响风力机信号共振解调故障诊断的问题,本文提出了一种压缩感知框架下的共振解调故障诊断方法。
(2)利用故障信号在傅里叶域稀疏度为2这一特点,通过傅里叶变换基和CS_SP算法对信号的包络特征进行不完全重构,直接获取反映故障特征的信号成分,从而提取信号故障特征频率。
(3)在仿真实验的基础上,选择1.5 MW直驱永磁风力发电机的滚动轴承故障振动信号进行实验,实验结果表明,压缩感知框架下的共振解调故障诊断方法能有效获取风力机滚动轴承的故障特征信息,验证了所提方法的有效性。
