螺栓结合部接触面域的融合绑定建模方法
2018-09-08崔方圆华灯鑫孔令飞李鹏阳
崔方圆 华灯鑫 李 言 孔令飞 李鹏阳
西安理工大学机械与精密仪器工程学院,西安,710048
0 引言
大型复杂结构体中广泛存在着各种类型的结合部,其中,螺栓结合部装拆方便、安全可靠,在机械结构中最为常见。螺栓结合部是指由螺栓紧固连接的两子结构间相互接触的部分。螺栓结合部的建模精度在整机动态性能的预测研究中至关重要,因为结合部的存在会导致结合区域处局部刚度的衰减和阻尼的增加,进而改变整机模型的动态性能[1]。研究结果表明,机床结构动力学建模误差主要来源于结合部的模型误差[2⁃5]。研究和解决如何精确、高效地构建合理的结合部模型有助于提升大型复杂结构动力学模型的建模精度,并为研究和预测复杂结构体的动态特征与性能评价奠定基础。
目前,从研究尺度上讲,结合部的研究方向主要分为微观基础理论研究和宏观工程应用两大类。前者主要是从粗糙表面的微观接触机理出发,基于经典的赫兹接触理论与分形模型,通过理论计算的方法来研究接触刚度与接触阻尼等结合部特性的变化规律[6⁃14]。然而,目前直接将微观基础理论研究的成果应用于复杂装配体模型的计算和预测中还具有一定的难度。另外,有限元分析方法的逐渐成熟为从宏观上研究螺栓结合部的建模问题提供了可能。与采用上述理论计算的方法相比,借助于现有的有限元软件从宏观的角度对结合部进行建模分析会更加简单方便,且通用性也会更好。传统的结合部有限元模型主要有以下3 种:刚性连接模型[15]、梁单元模型[2]和黏弹性单元模型[16]。一般来说,第一种模型过于简单,忽略了子结构间的非连续性,因此,在进行机械结构动力学分析时,所产生的结果与实际情况之间的误差较大。第二种模型仅适用于特定梁属性的结合部,受结合部尺寸形状变化的局限性较大。目前在结合部建模时普遍采用第三种模型。有限元分析方法虽然简单有效,但在实际应用中却存在一个较大的缺陷,即无法准确确定结合面之间所需建立的连接点数量及其分布位置,而实际上连接点的分布情况对有限元计算结果有较大的影响。
近年来,虚拟材料层法越来越受到学者们的青睐[17⁃19],该方法为从宏观上进行结合部建模提供了一种新思路,具有重要意义。T IAN等[17]基于赫兹接触理论和分形模型理论,推导了虚拟材料层的弹性模量、泊松比和密度的计算模型。贾文锋等[19]根据粗糙表面的形貌特征和结合部法向和切向的不同特性,提出了基于横观各向同性虚拟材料假设的固定结合部等效建模方法。虚拟材料层法本质上是在两个相互配对的子结构间添加一层具有一定厚度的虚拟介质,再依据结合部的特性赋予该虚拟介质层相应的材料属性。但虚拟材料层的构建无疑会在改变结构尺寸的同时增加模型的质量,致使系统整体自由度变大,这就给系统的振动分析和性能评价带来诸多不便。
为克服上述缺陷,本文提出了一种螺栓结合部接触面域的融合绑定建模方法。该建模方法最大的特点是不会改变模型原来的质量和尺寸,由此可有效避免增加复杂结合部模型求解的自由度数,并且参数识别方便,通用性强,具有较高的建模精度。
1 接触面域单元法基本理论
CˇELICˇ等[20]指出,当以标准扭矩拧紧螺栓并对结构体进行小幅激励时,被连接结构之间的非线性行为会受到抑制,此时可以忽略螺栓结合部非线性特性的影响。由于在工程结构应用中,螺栓连接件多为紧固连接,故本文主要研究螺栓结合部的线性动力学特性,不考虑螺栓结合部之间的滑移、阻尼及其他非线性特性。在其线性特性范围内,螺栓结合部对整机动态性能的影响主要表现在连接区域所产生的局部刚度弱化效应,这是因为虽然螺栓仅作用于固定点,但影响却是区域性的[21]。从某种程度上讲,弹性模量恰恰可以从宏观的角度表征物体的刚度,由此可以用连接区域中材料属性的变化来等效表征结合部在其线性特性范围内最主要的物理特征,即局部刚度弱化效应。
对于不同的分析对象,螺栓结合部通常有以下两种处理策略:①如果只关注整体结构的特性,螺栓部分可以用连接单元作简化处理;②如果关注螺栓局部的强度,则需建立较为完整的螺栓模型。接触面域的融合绑定建模方法着眼于结合部对整体结构的影响,由此采用简化的螺栓建模策略。为了建模方便,建模时忽略了螺栓孔的影响,将螺栓结合部的接触面积等效为整个连接区域的接触面积,并假设刚度弱化影响仅集中于接触面两侧子结构内的某个等效区域内,该等效区域称为螺栓结合部影响区域[22]。螺栓结合部影响区域的示意图见图1。
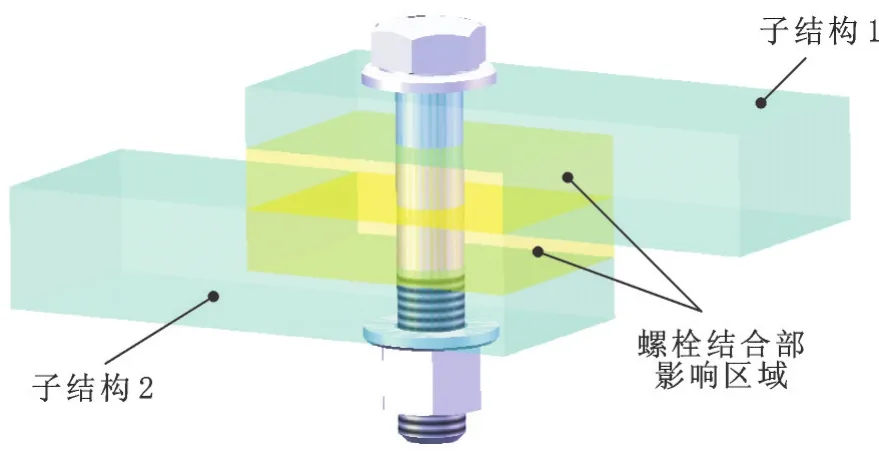
图1 螺栓结合部影响区域Fig.1 Bolted joint affected region
接触面域的融合绑定建模方法就是基于上述螺栓结合部影响区域的概念,用简化处理过的双层接触面域单元来等效模拟螺栓结合部复杂的线性动力学特性。建模过程中,由配对子结构在接触面两侧各提供一部分单元组成接触面域单元。通过对该区域单元的等效处理,使其满足各向同性条件,而接触面域单元之间则被构建为融合绑定接触连接。融合绑定接触连接是指两侧的接触面域单元之间的接触方式为绑定接触,上下对应单元之间的节点融合为同一个节点。为了体现该建模方法与虚拟材料层法的区别和优势,图2示出了虚拟材料层法和接触面域的融合绑定法的简单建模过程。对比后可以看出,与添加虚拟材料层相比,采用接触面域单元建模有以下3个优点:①接触面域单元是由接触面两侧的子结构各提供一部分单元所构成的,由此不会改变整体模型的尺寸,也不会增加模型的求解自由度数;②在对大型复杂结构进行整机建模时,构造虚拟材料层需要重新对整个模型进行再装配,而采用接触面域单元进行建模,只需对子结构进行微小的调整,所以其操作具有简便性;③虚拟材料层法建模会增加结构的整体质量,而接触面域单元建模只要使接触面域单元的密度等于子结构中其他部分单元的密度,整体模型的质量分布情况就不会改变,进而不会影响到结构原来的动力学特性。上述特点在包含很多结合部的大型复杂结构整机有限元模型的建模过程中无疑是非常必要的。
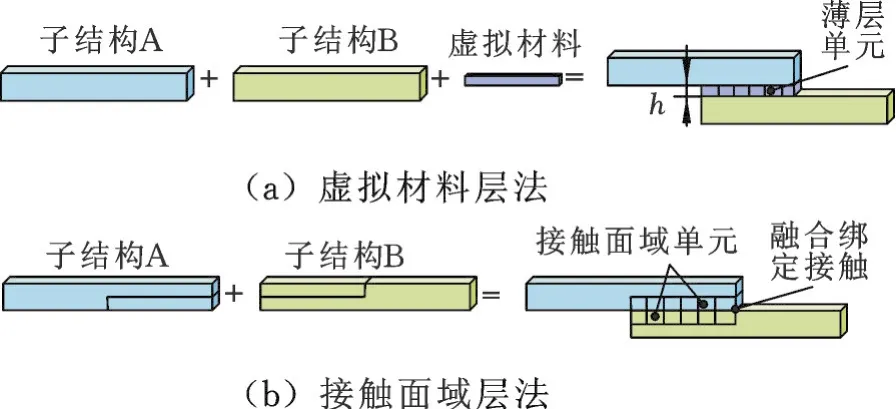
图2 2种方法的对比Fig.2 Com parison of two app roaches
2 有限元模型的建立
研究对象由2块尺寸相同的钢板通过2个螺栓搭接而成,所采用的螺栓型号均为M 12,性能等级为4.8,通过力矩扳手对2个螺栓施加同样的预定扭矩28 N·m。钢板的长度均为432 mm,矩形截面尺寸为45 mm×8 mm,螺栓结合部连接区域的尺寸为32mm×45mm,整个连接结构的几何尺寸和搭接情况见图3。

图3 双螺栓搭接梁结构尺寸Fig.3 Geometrical dim ensionsof overlapped assem b ly
下文进行的锤击模态实验的几何建模过程中所采用的建模方式为直线建模方式,激励方式为沿y方向垂直激励,故实验测量结果实际上与有限元模型在竖直平面oxy内的弯曲模态所对应。为了保证在感兴趣的频率范围内所有模态振型均在oxy平面内,方便定性地比较实验模态振型和有限元计算得到的理论模态振型,在有限元模型中沿模型的z向施加一个零位移约束,见图4。该零位移约束可以保证模型沿z方向不会产生任何结构位移,进而避免了模型在oxz平面内的所有横向弯曲和扭转模态。此外,模型的轴向模态也不在本文考虑的范围内。

图4 模型z向施加的零位移约束Fig.4 Zero d isp lacem en t constrain t in z direction
采用接触面域的融合绑定建模方法对双螺栓搭接结构基础试件划分完网格后的有限元模型见图5。所采用的单元是20节点的三维固体单元(solid 186),单元尺寸为3.2mm,划分网格后得到的总单元数目为17 280,节点数目为85 793。在整个有限元模型中共定义2种材料参数。由图5可以清楚地看到,在初始有限元模型中,为了建模方便,将接触面域单元的厚度设置为子结构中性面之间的距离。在接触面域单元所在的区域内定义各向同性材料参数1,弹性模量为E1;其他非接触区域定义各向同性材料参数2,弹性模量为E2。在初始有限元模型中,接触面域单元的弹性参数E1与非接触单元的弹性参数E2相同;接触面域单元的密度ρ1与非接触单元的密度ρ2相同,这是为了保证在建模时不改变模型原有的质量分布情况,进而不影响结构原有的动力学特性。

图5 螺栓结合部有限元模型Fig.5 Finite elem entmodel of bolted joint
为了研究螺栓螺母及传感器的附加质量对计算结果精度的影响,分以下2种情况对该初始有限元模型进行初步研究:①完全忽略螺栓螺母和传感器的附加质量;②将上述附加质量在有限元模型中用点质量来代替。2种情况下模态分析计算获得的前6阶固有频率结果见表1,相应的理论振型见表2。

表1 实验结果与有限元计算结果对比Tab.1 Com parison between experim en tal results and FE calculation resu lts
3 模态实验
3.1 实验原理及现场布置
结构的固有频率、振型及频响函数是描述其动态特性的主要参数,获取上述参数最直接有效的方法是对包含结合部在内的待测结构进行模态实验。各种模态分析软件的相继出现为结构的模态分析和应用提供了很大便利,使得设计者能够采用多种手段对结构的动态特性进行测量和分析。本文采用LMS Test.Lab振动测量和分析系统对双螺栓搭接结构结合部基础试件进行锤击法模态实验。
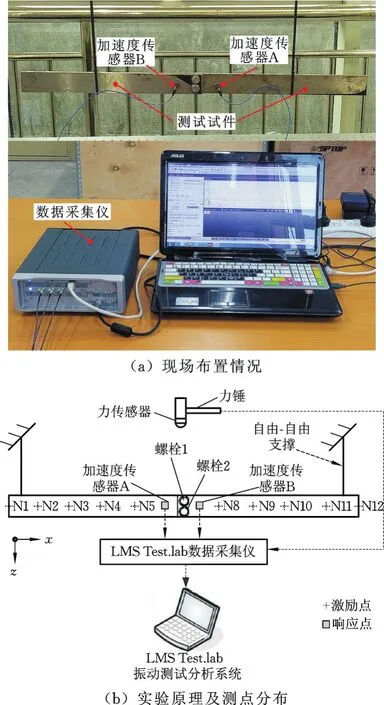
图6 测试现场及实验原理Fig.6 Practical test situation and experimental p rincip le
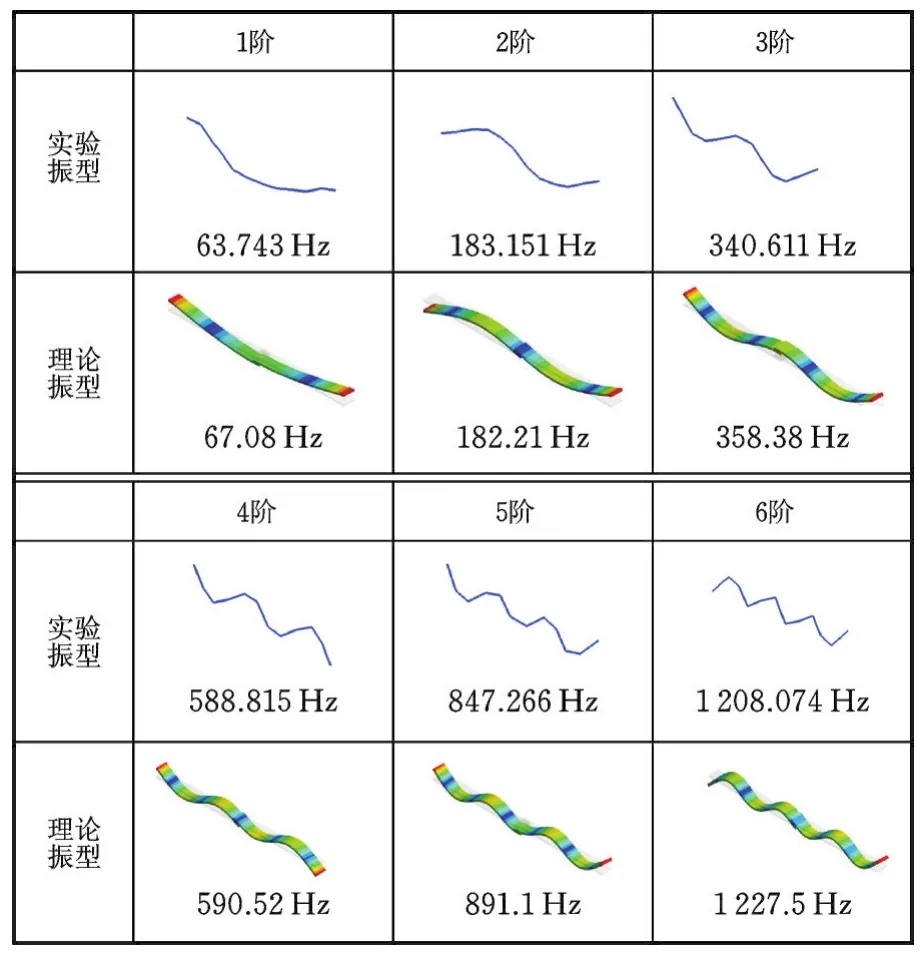
表2 理论与模态实验振型对比Tab.2 Com parison of the experim en talm ode shapes and theoreticalm ode shapes
在进行模态实验时,除非有可能模拟待测结构所处的实际边界条件,否则一般都考虑使其处于自由状态下进行实验。在本研究中用2根弹性绳将双螺栓结合部基础试件悬挂起来,用以模拟系统的自由-自由边界条件,见图6a。实验原理图和测点在待测结构上的具体分布情况见图6b。由图6b可以看出,该动态特性实验装置包括:双螺栓结合部基础试件、力锤、加速度传感器、LMS Test.Lab振动测量和分析系统、PC机以及信号线等仪器和设备。在实验过程中,激励力的大小由内置安装在力锤前端的力传感器直接测量得到,待测结构的响应信号则由对称安装在螺栓结合部两侧的加速度传感器A和B进行采集。传感器采用对称安装是为了使待测结构处于平衡状态,尽可能减小附加质量对计算结果精度的影响。传感器均为PCB公司生产的333B30型加速度传感器,参考灵敏度为100.5 m V/g,频率范围为0.5~3 000 Hz,质量为4 g。由于待测结构中共有两个响应点和12个激励点,故采用多点激振两点拾振的方法对图6b中的每个测点进行锤击激励。为了尽可能减小实验随机误差带来的影响,提高实验数据的可靠性,手持力锤对每个激励点沿y方向垂直激励3次。
用LMS Test.Lab振动测量和分析系统对采集到的数据信号进行分析处理。频率范围取0~1 900 Hz。通过峰值拾取法得到的前6阶实验固有频率见表1。这些模态实验固有频率用来与初始有限元模型仿真计算获得的固有频率进行对比,也是后续螺栓结合部物理表征参数识别过程中构建目标函数的依据。获得的实验模态振型见表2,并与上文得到的理论振型作对比。
模态置信判据(modal assurance criterion,MAC)是检查两模态振型向量一致性的一个数学准则,与系统矩阵无关,常用来验证模态分析结果的精度。M AC值计算公式为

计算2个模态振型向量之间的M AC值,就相当于近似地检验它们之间的正交性。如果复向量Rjk与Rlk之间存在线性相关,则MAC值接近100%;如果两者是线性独立的,则MAC的计算值很小(接近于零)。本实验结果所获得的各阶模态振型向量之间的MAC三维柱状图见图7,其中,较高的柱体部分为各阶振型向量与自身的正交性检验结果,其值全为100%;其余部分的最大值不足15%,由此可见前6阶模态振型向量之间的相关性很小,说明实验结果较为准确。
3.2 结果对比分析
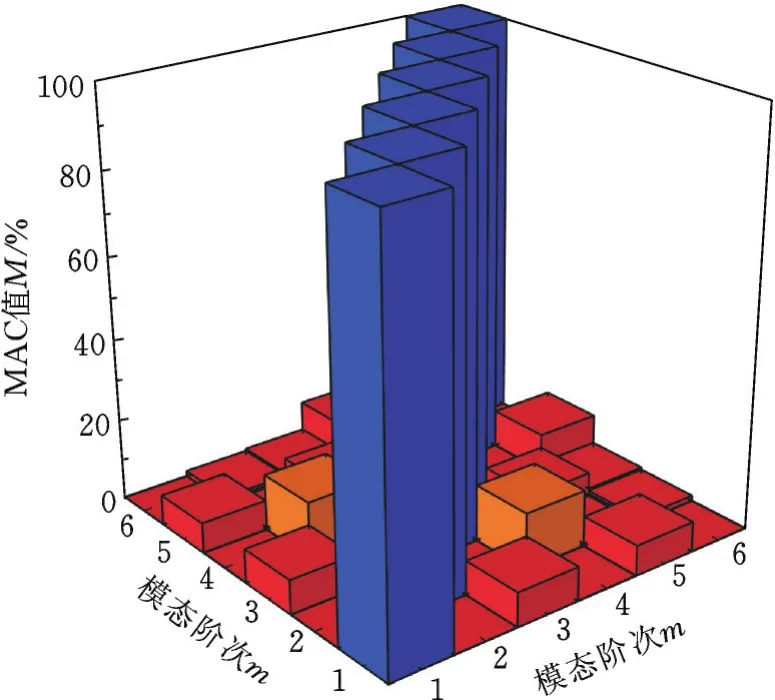
图7 M AC图Fig.7 Bar chat of MAC
考虑到模态分析计算的振型是研究结合部动力学建模方法的参考基准之一,本文首先定性对比模态实验测试和有限元仿真计算得到的模态振型。对比表2可知,在上述感兴趣的频率范围内,有限元仿真计算获得的前6阶理论模态振型与实验振型完全一致且一一对应。基于一致的模态振型,再定量对比分析表1中的前6组固有频率的仿真值和实验值。经过对比,可以得出以下结论:
(1)螺栓螺母和传感器的附加质量对计算精度有较大影响。未考虑螺栓螺母及传感器的附加质量时,初始有限元模型计算出的固有频率与实验值之间误差较大,总误差约18.04%;而将这些附加质量用点质量来代替再进行模态计算时,固有频率之间的总误差降至15.61%。此外,还可以看出附加质量对低阶固有频率的影响较大。因此,在对含有多个螺栓结合部的大型复杂结构进行建模时,需要将传感器和螺栓螺母的附加质量考虑在内,否则计算结果会产生较大误差,进而影响到整机动态特性分析的精度。鉴于此,下文中螺栓结合部物理表征参数的优化识别都是基于考虑螺栓螺母和传感器质量的有限元模型。
(2)可以看出,在感兴趣的频率范围内,除了第3和第5阶固有频率外,其余各阶固有频率之间的误差都较小。但从总体上来看,实验固有频率与其对应的计算值之间并不存在较大误差(误差均小于6%)。这是因为,为确保子结构的分析模型与物理模型之间协调一致的精度,分别在自由⁃自由边界下对2个子结构进行了模态实验。初始有限元模型中子结构的弹性模量都是依据模态实验结果优化识别后得到的。这样就最大程度地减小了由子结构的不稳定性导致的建模误差,从而确保了整个装配结构的动力学建模误差主要是由螺栓结合部的模型误差引起的。
4 结合部物理表征参数的优化识别
4.1 识别原理
系统的频响函数和固有频率都是其动态特性的本质表征,与系统的输入输出无关,所以可用作系统模态参数的识别依据。一般情况下,固有频率被认为最容易准确得到,因此,目标函数的优化工作往往从寻求固有频率开始。螺栓结合部物理表征参数优化识别原理见图8,其基本思想如下:①首先采用锤击法对双螺栓结合部基础试件进行自由模态实验,获取其前若干阶固有频率和模态振型,为有限元仿真模态分析提供参照和基准;②采用接触面域的融合绑定法在有限元软件ANSYS中对双螺栓结合部基础试件进行建模,获取初始有限元模型的理论固有频率和模态振型;③使用APDL(参数化设计语言)建立目标函数;④以接触面域单元的弹性模量E、接触域厚度h和泊松比μ为设计变量,基于多目标遗传算法(MOGA),对螺栓结合部物理表征参数进行优化识别;⑤将识别结果回代到有限元软件中,通过自动寻优的方法从模态分析计算的多组优化结果中找出最接近基准实验模态的固有频率,此时的最优设计变量值即为待识别的螺栓结合部物理表征参数。
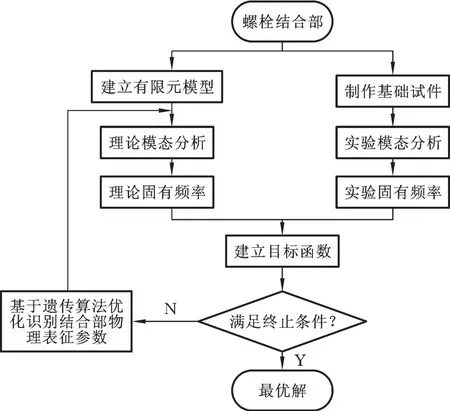
图8 螺栓结合部物理表征参数识别原理Fig.8 Identification p rincip le for physical characterization param eters of bolted join ts
目前在工程设计中,利用遗传算法对有限元模型进行优化和修正越来越受到人们的青睐[23⁃24]。本文所进行的螺栓结合部物理表征参数的优化识别工作是基于多目标遗传算法进行的。这种多目标优化技术是从给出的一组样本(即一定量的设计点)中得出“最佳”的设计点,进而来研究设计变量和目标函数之间的关系。
构建目标函数时,本文采用与文献[25⁃29]相似的思想,即以实验固有频率和理论固有频率两者之间的最小相对误差平方和为目标函数,其表达式如下:

其中,Wi为第i阶固有频率所对应的权重系数,权重系数的设置原则是每个权数均大于或等于零且各权重系数之和为1;ωFEi、ωEXPi分别代表有限元计算固有频率和实验固有频率。在目标函数中采用加权的方法可以充分利用各阶固有频率,从而提高辨识精度。本文对每阶固有频率的关注度是一样的,故每阶固有频率的权重系数均为0.25。由式(2)可知,第5阶和第6阶固有频率并没有参与目标函数的优化识别过程,目的是验证所使用的方法对高阶模态预测同样有效。
在优化前需要先定义设计变量。接触面域单元的弹性模量、接触域厚度h和泊松比μ是接触面域融合绑定法所涉及的几个重要参数,因此将这些参数作为设计变量,各设计变量的参数变化范围见表3。

表3 设计变量及其变化范围Tab.3 Variations and their perm issib le ranges
4.2 最优化求解及识别结果
在表3中设计变量的变化范围内,基于多目标遗传算法对螺栓结合部物理表征参数进行优化识别。目标函数在优化过程中的收敛历程曲线见图9,可以看出,每个迭代步有50个设计点,目标函数经过7次迭代后收敛。
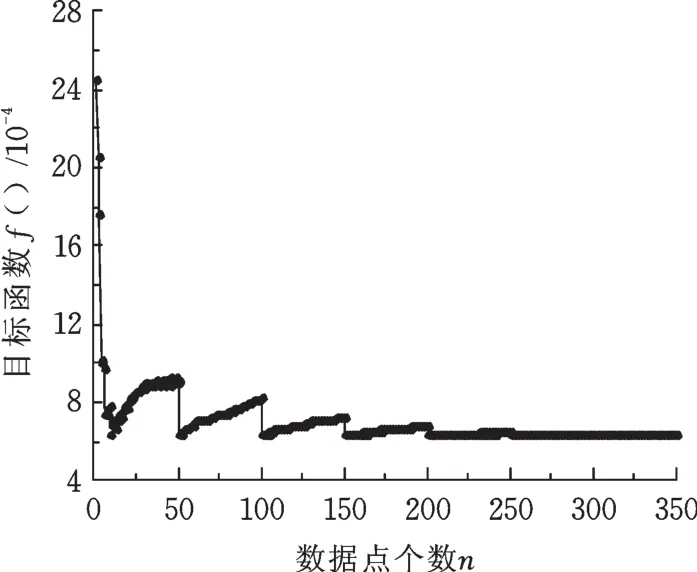
图9 目标函数收敛历程Fig.9 Convergence p rocessof objective function
3个设计变量(弹性模量E、接触面域单元厚度h和泊松比μ)的收敛历程曲线分别见图10~图12。

图10 弹性模量收敛历程Fig.10 Convergence p rocess of elasticmodulus
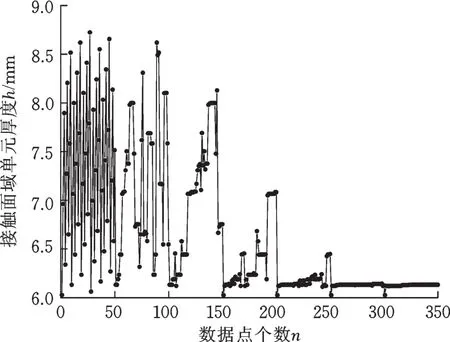
图11 接触面域单元厚度收敛历程Fig.11 Convergence process of con tact area elem ent thickness

图12 泊松比收敛历程Fig.12 Convergence p rocessof Poisson ratio
螺栓结合部物理表征参数的优化识别结果见表4,可以看出,接触面域单元的材料特性在优化识别后产生了非常明显的变化,该区域单元材料的弹性模量与初始值相比减小了约1/5。弹性模量可以从宏观的角度表征结构的刚度,故接触面域单元中弹性模量的减小等效体现了螺栓结合部的局部刚度弱化效应。最终得到的接触面域单元的最优厚度约为6 mm,与初始值相比减小了约2 mm。而泊松比在优化识别前后并没有产生较大的改变,这是因为在模态实验的过程中,激励方式为垂直小幅激励,在剪切方向并没有产生滑移,因此,其值也基本保持不变。

表4 螺栓结合部物理表征参数Tab.4 Physical characterization param eters of bolted joint
将表4中所识别的螺栓结合部物理表征参数回代到初始有限元模型中并对模型进行修正,修正结果见表5,可以看出,优化识别后,实验固有频率和其对应的计算固有频率之间的总误差从15.61%减小到13.57%,这说明该建模方法可以在一定程度上进一步提高有限元模型与物理模型之间协调一致的精度。此外,第5阶和第6阶固有频率之间的相对误差也明显减小,这说明该建模方法对预测高阶模态同样有效。
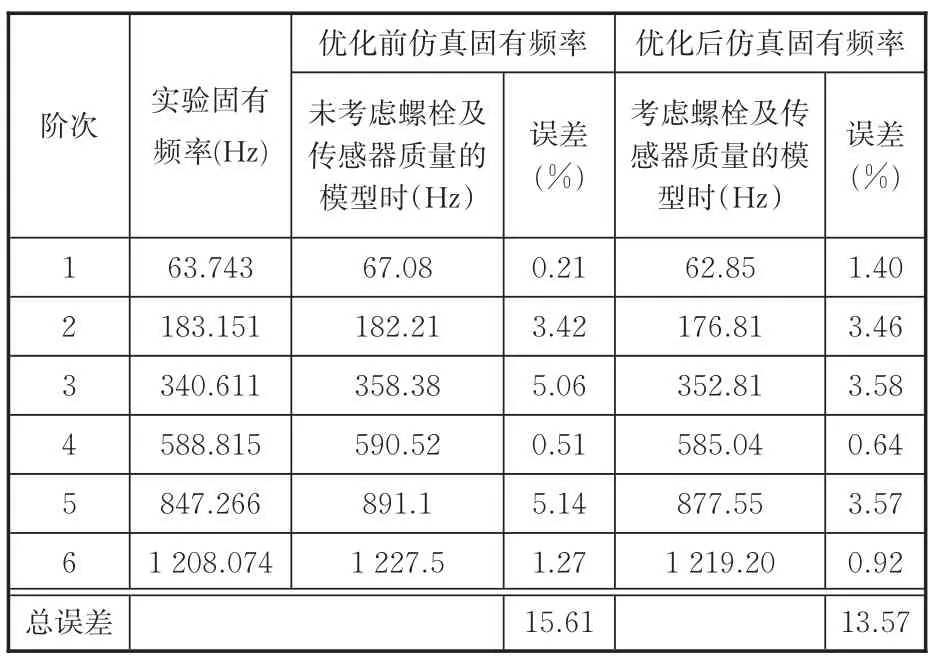
表5 优化前后固有频率结果对比Tab.5 Com parison of natu ral frequencies before and after op tim ization
综上所述,基于各向同性材料的接触面域单元能够较好地表征螺栓结合部的局部刚度弱化效应,从而验证了本文所提出的建模方法的有效性与可行性,为精准、高效地预测复杂结构连接体的动态特征与性能评价提供了一种简单、有效的分析途径。
5 结论
(1)提出了一种螺栓结合部接触面域的融合绑定建模方法。该建模方法最大的特点是不会改变模型原来的质量和尺寸,故可以有效避免增加复杂结合部模型求解的自由度数,并且参数识别方便,通用性强,具有较高的建模精度。
(2)研究结果表明,螺栓螺母和传感器的附加质量对计算结果精度有一定的影响。因此,对含有多个螺栓结合部的大型复杂结构进行建模时,需要将螺栓螺母和传感器的附加质量考虑在内,否则会使计算结果产生较大的偏差,进而影响到整机动态特性分析的精度。
(3)不考虑螺栓结合部剪切方向上的滑移带来的非线性时,结合部的建模精度主要依赖于接触面域单元的弹性模量和厚度这2个参数,而泊松比对计算结果的影响很小。参数识别结果还表明,存在一个接触面域单元的最优厚度,该参数由模型优化过程所决定。接触面域单元的弹性模量约为初始值的1/5,这等效表征了螺栓结合部的局部刚度弱化效应,这也是螺栓结合部在其线性特性范围内最主要的特征表现。
(4)仿真结果表明,使用该种建模方法可以提升有限元模型与物理模型之间协调一致的精度,从而验证了该建模方法的有效性和可行性。此外,本文所提出的结合部建模方法对预测高阶模态同样具有有效性,这为大型复杂结构整机动力学分析提供一种简单、有效的分析途径。
