橡胶沥青混合料疲劳损伤及全周期寿命预估
2018-09-07申爱琴喻沐阳周笑寒吕政桦
申爱琴, 喻沐阳, 周笑寒, 吕政桦, 宋 攀
(长安大学 公路学院, 陕西 西安 710064)
废旧橡胶是一种难以降解的高分子材料,其回收和处理技术是世界性的难题.使用废旧轮胎胶粉生产橡胶沥青是减少“黑色污染”最有效方法之一,而且橡胶沥青混合料高低温性能优异,抗疲劳开裂能力较强,因此被广泛应用于高等级公路沥青路面工程[1].
沥青混合料疲劳性能评价主要通过室内疲劳试验的方法,其中4点弯曲疲劳试验适用范围广,并被国内外规范采纳为标准试验方法[2],其劲度模量随加载次数的关系即疲劳损伤曲线是疲劳性能评价及寿命预估的重要依据[3].吴志勇等[4]认为沥青混合料疲劳失效时劲度模量衰减比与其公称最大粒径和应变水平有关,均小于50%.ASTM D7460认为在归一化复合模量次数达到峰值时发生疲劳失效[5].AASHTO T321选用指数函数S=AeBN来拟合损伤曲线,将劲度模量下降至初始值50%即A/2作为疲劳失效判定标准[6].平树江等[7]对该方法进行了改进,仅选取损伤发展阶段的劲度模量数据建立回归方程,取得了更理想的寿命预估效果.然而Rowe等[8]认为传统的50%判定法并不能准确评价沥青混合料的疲劳性能,疲劳失效发生在劲度模量下降至初始值35%~65%之间.
综上所述,现有研究大多集中于沥青混合料疲劳失效判定标准和疲劳寿命计算方法,失效判定标准不统一,导致寿命计算结果相差较大,而且针对疲劳性能评价指标研究较少.橡胶粉的加入提高了集料与沥青的黏结性,使其具有一定的自愈合能力[9],采用原寿命评价方法和理论难以准确评价其疲劳性能.有鉴于此,本文采用橡胶沥青混合料进行4点弯曲疲劳试验,通过分析劲度模量与疲劳荷载作用次数的关系来研究其疲劳损伤过程,计算疲劳曲线特征值,将其作为评价指标,并提出疲劳性能阶段性评价方法.最后提出疲劳寿命全周期预估方法,并借助BP神经网络模型进行全周期疲劳寿命预测.
1 试验材料和方法
1.1 橡胶沥青的制备
橡胶沥青采用热熔法加工;基质沥青采用韩国SK牌90#沥青;橡胶粉粒径为0.600mm,均采用900型以上的斜交轮胎常温研磨加工而成.本文对不同胶粉掺量1)的橡胶沥青进行配伍性试验,试验结果如表1所示.由表1可见,橡胶沥青各项性能均满足技术要求,根据已有工程经验,并参考胶粉掺量与疲劳自愈合效率的关系[9],确定胶粉掺量(外掺)为20%.

表1 橡胶粉与沥青配伍性试验结果
1.2 橡胶沥青混合料设计与成型
1)本文所涉及的掺量、油石比等均为质量分数或质量比.
粗集料为商州汇金石料厂生产的辉绿岩,规格分别为9.50~16.00mm,4.75~9.50mm,2.36~4.75mm,技术指标见表2;细集料为蒲城泉沟产石灰岩机制砂,规格为0~2.36mm;填料为蒲城泉沟产石灰岩矿粉;外加剂为0.3%抗车辙剂.

表2 试验用粗集料技术指标
本文在橡胶沥青混合料组成设计时,选用AR-SMA-13骨架密实型级配,这样既保证了粗集料充分嵌挤形成骨架,使橡胶沥青合理填充于骨架空隙内,又保证了橡胶粉不会对骨架结构产生干涉作用.合成级配及级配范围见表3.
橡胶沥青混合料设计采用马歇尔设计方法,设计空隙率(体积分数)为4%,最佳油石比为6.3%,最佳沥青掺量为5.9%.路用性能测试结果见表4.由表4可知,橡胶沥青混合料的高温稳定性、低温抗裂性和水稳定性都满足规范要求.其中水稳定性得到明显改善,残留稳定度达到101%,整体路用性能良好.

表3 橡胶沥青混合料的合成级配及级配范围

表4 橡胶沥青混合料路用性能试验结果
1.3 疲劳试验方法
本文采用应变控制4点弯曲疲劳试验,能够客观评价车辆荷载对路面疲劳性能的影响,并被国内外大多规范采纳.首先,采用小型压路机成型尺寸300mm×400mm×70mm沥青混凝土板,然后切割成尺寸380.0mm×63.5mm×50.0mm的小梁试件,成型好的试件如图1所示.试件加载采用澳大利亚生产的BFA疲劳试验装置.控制器和数据采集采用UTM伺服液压多功能材料试验系统,该系统配备UTS试验软件.测试过程如图2所示.

图1 疲劳试件Fig.1 Fatigue specimen

图2 疲劳试验测试过程Fig.2 Fatigue test process
本文疲劳试验参数设定参考AASHTO T321-07,试验温度为20℃,考虑到沥青路面实际状况和试验设备参数设定范围,将应变水平ε设定为400,600,800,1000μm·m-1.选用循环加载第50次时的劲度模量作为初始劲度模量.为获得橡胶沥青混合料完整疲劳损伤曲线,本文将试验终止条件设定为劲度模量衰减到初始值20%,最大加载次数为250000次.
2 橡胶沥青混合料疲劳损伤评价
2.1 疲劳损伤演化过程分析
在疲劳荷载作用下,沥青混合料内部结构产生损伤,可表现为劲度模量不断衰减.图3为沥青混合料典型疲劳试验结果.由图3可知:疲劳损伤演化过程可分为初始预热、微裂纹扩展、宏观裂缝形成、试件断裂4个阶段[8],而且弯拉劲度模量衰减至初始值50%左右时会出现性能劣化速度加快的现象,即发生了疲劳失效.图4为橡胶沥青混合料疲劳试验结果.
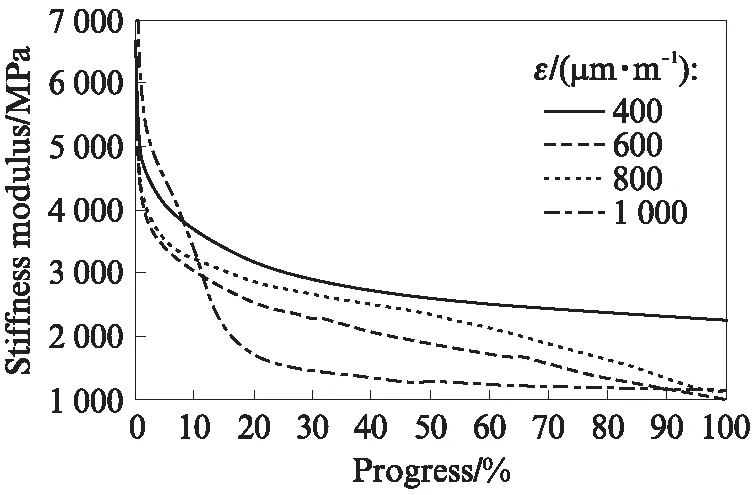
图4 橡胶沥青混合料疲劳试验结果Fig.4 Fatigue test result of rubber asphalt mixtures
由图4可知,橡胶沥青混合料在不同应变条件下的疲劳损伤演化过程趋势相似,劲度模量随加载次数的增加迅速降低.但直至劲度模量衰减至初始值的20%时,试件也未出现明显的损伤速度加快疲劳失效现象.橡胶沥青混合料表现出了良好的抗疲劳性能.究其原因,这是因为采用热熔法生产的橡胶沥青中胶粉分布均匀,胶粉中含有的天然橡胶、硫磺、碳黑等成分是沥青的良好改性剂,可有效提高沥青的柔韧性,并对其弹性恢复性能有显著改善,同时采用了骨架密实性结构,充分发挥了橡胶沥青的性能优势.
2.2 失稳阶段损伤评价
疲劳试验刚开始阶段,结构内部局部区域应力集中、裂缝不断扩展,从而使其劲度模量急剧减小,导致实际应变水平与设定值存在一定误差,本文剔除应变误差大于10μm·m-1的试验数据.选择幂函数S=ANV+S0为回归方程,其中疲劳加载次数N作为自变量,弯拉劲度模量S为因变量,并借助OriginPro 9.1曲线拟合功能对试验数据进行回归分析.回归方程中:A为拟合参数,取决于材料性质;V代表失稳阶段试件衰减速率即失稳率;S0为基于整体试验数据预测的无损劲度模量,幂函数回归结果见表5.表5中,SSE为和方差,RMSE为均方根.
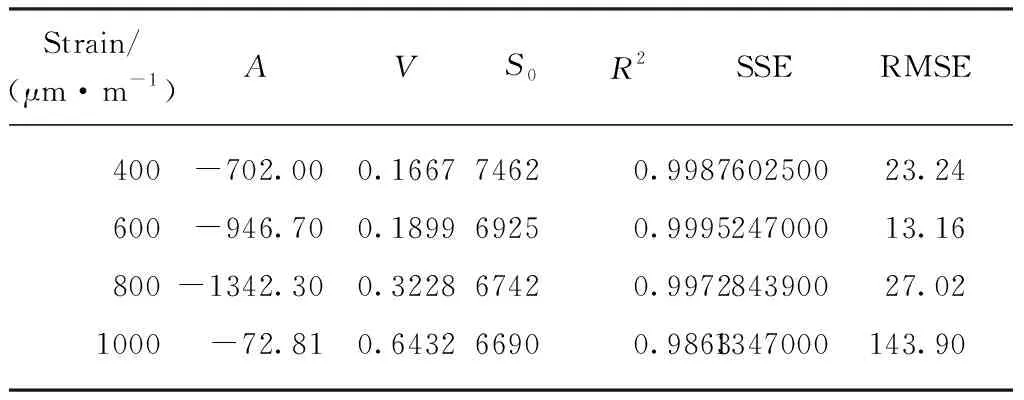
表5 失稳阶段幂函数回归结果
由表5可知:失稳阶段幂函数回归相关性较高,相关系数均高于0.98,说明采用幂函数性质表征橡胶沥青混合料失稳阶段疲劳性能具有较高的可靠度;随着应变水平的增加,单位疲劳荷载造成的损伤加大,表现为失稳率V大幅增加,与400μm·m-1应变水平相比,600,800,1000μm·m-1应变水平下分别增加了13.92%,93.64%,285.84%,这与实际情况是吻合的;S0在高应变水平下略有降低,与400μm·m-1应变水平下相比,降幅最大达10.35%.
2.3 稳定发展阶段损伤评价

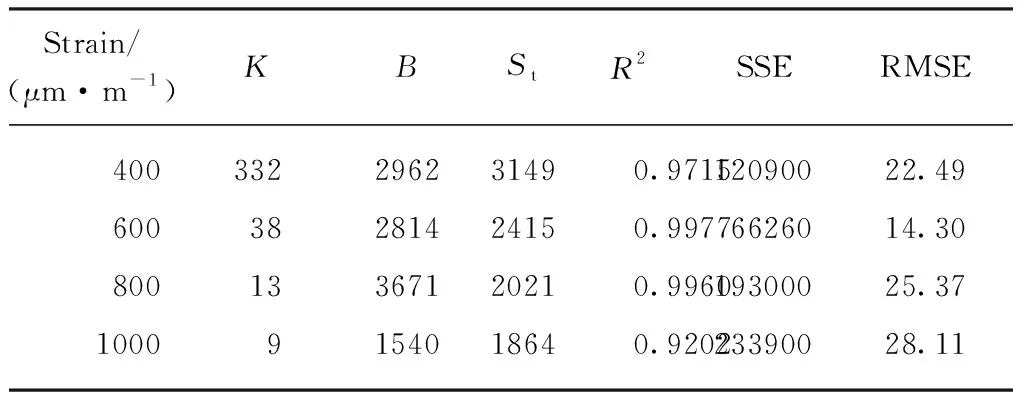
表6 稳定发展状态直线回归结果
由表6可知,各应变水平下的回归结果相关系数均大于0.9,其中400~800μm·m-1应变水平下达到0.97以上,1000μm·m-1应变水平下相关系数仅为0.9202.究其原因,是因为高应变水平荷载作用下,材料性能劣化速度加快并在试验过程中产生轻微震动,导致劲度模量测量结果波动性较大.随着应变水平的降低,疲劳稳定度K大幅度增加,与1000μm·m-1应变水平相比,400,600,800μm·m-1应变水平下分别增加了35.84,3.22,0.39倍.与此同时转化劲度模量St不断增加,说明低应变水平下材料能够更好地抵抗失稳阶段劲度模量急速衰减的状态.
3 基于神经网络模型的全周期疲劳寿命预估
3.1 BP神经网络模型设计
橡胶沥青混合料疲劳损伤过程未产生明显的劣化加速现象,鉴于此,笔者认为橡胶沥青疲劳寿命应包括疲劳裂纹产生并不断扩展直至失去承载力的全周期损伤过程,并采用劲度模量衰减为零作为失效判定标准.不同应变水平下试件损伤过程差异性较大,采用固定函数模型拟合难以取得理想拟合效果.BP神经网络具有高度自学习和自适应能力,只要隐含层节点数够多,模型可以以任意精度逼近任意具有有限间断点的非线性函数[10].因此本文借助BP神经网络模型进行预估.
本文选择含有输入层、隐含层、输出层的3层前向反馈神经网络模型.图5为具有一个隐含层的3层BP神经网络拓扑结构图.
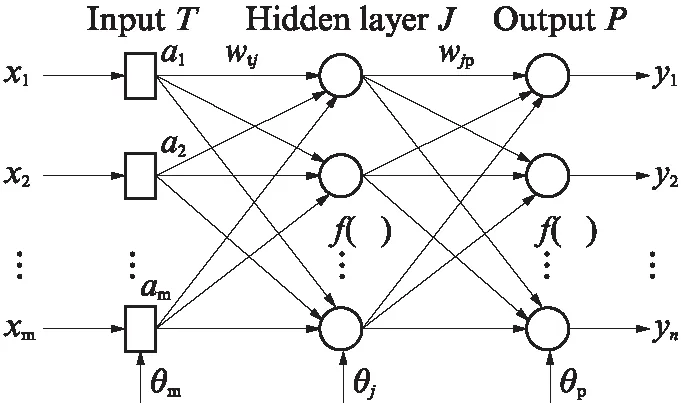
图5 BP神经网络拓扑结构图Fig.5 BP neural network topology chart

3.2 全周期寿命预测神经网络模型分析
为对神经网络模型进行优化并提高其泛化能力,本文采用Levenberg-Marquardt,Scaled conjugate gradient,Bayesian regularization 3种训练算法,按照设定参数建立神经网络模型,最后计算全周期疲劳寿命.本文采用迭代次数、最大相对误差(MAX RE)、误差平方和(SSE)作为神经网络模型预测性能评价指标.不同训练算法寿命预测结果见表7.由表7可知:不同算法模型预估结果有一定差异,但最大误差均小于10%,全周期疲劳寿命预测精度较高,相比之下Levenberg-Marquardt函数收敛速度较快,经过12~127次可结束训练,而且误差平方和明显低于其他算法,最大相对误差为1.70%~ 8.23%.

表7 不同训练算法神经网络疲劳寿命预测结果
图6为400μm·m-1应变水平下橡胶沥青混合料全周期寿命预估误差分布.由图6可知:目标值与预测值的误差呈现正态分布特征,正负误差相当,而且误差值集中在-1000~1000次之间,占数据总量84.48%,误差绝对值大于3000次的比例为4.42%,相对于最大加载次数250000次,预测误差在可接受范围之内.神经网络模型可靠度较高,采用其进行橡胶沥青混合料全周期疲劳寿命预估可以得到比较准确的结果.将预测结果在双对数坐标下建立橡胶沥青混合料疲劳寿命-应变水平(Nf-ε)方程,如图7所示.由图7可见:随着应变水平ε的增加,橡胶沥青混合料疲劳寿命Nf大幅降低,而且在双对数坐标轴上两者存在良好的线性相关性,相关系数为0.9736.

图6 全周期寿命预估误差分布Fig.6 Full-cycle life expectancy error distribution
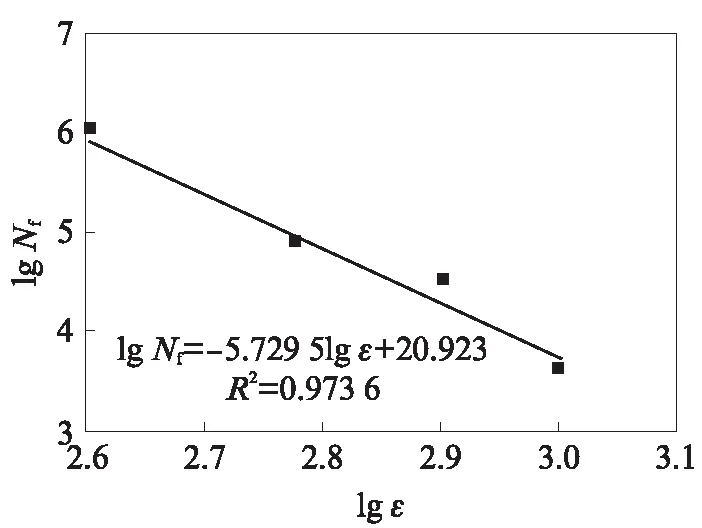
图7 全周期疲劳寿命方程Fig.7 Full cycle fatigue life equation
4 结论
(1)橡胶沥青混合料疲劳性能与普通沥青混合料相比有较大差异,其疲劳损伤曲线未呈现4阶段发展过程,材料性能劣化速度能够保持在稳定发展状态,劲度模量下降至初始值20%时未出现明显的疲劳失效现象.
(2)橡胶沥青混合料疲劳曲线特征值可作为疲劳性能评价指标.采用无损劲度模量S0,失稳率V,疲劳稳定度K和转化点劲度模量St综合评价其疲劳性能可信度较高,相关系数均在0.92以上.
(3)BP神经网络模型预测橡胶沥青混合料全周期疲劳寿命可获得较准确结果,Levenberg-Marquardt函数训练算法收敛速度快,泛化能力好,最大相对误差为1.70%~8.23%,全周期疲劳寿命与应变水平在双对数坐标轴上有较好的线性相关性.
