一道高考试题的赏析及教学启示*

●

(砀山中学,安徽 砀山 235300)

1 试题呈现

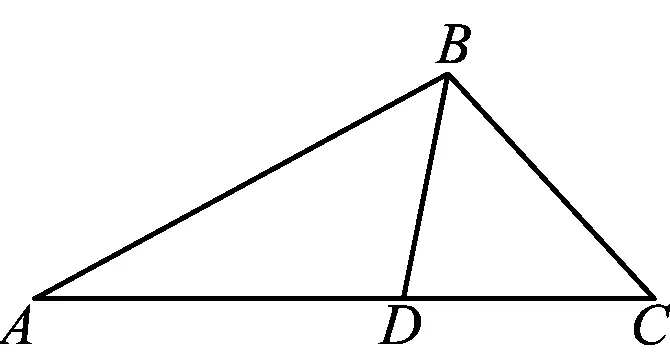
图1

题目如图1，在△ABC中，角A,B,C所对的边分别为a，b，c,∠ABC=120°,∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为______.

(2018年江苏省数学高考试题第13题)

2 试题赏析

该试题是以解三角形为背景的最值问题，呈现方式常规但又不俗套，表述清楚，简洁明了，给人一种平和中见亲切、简明中见关怀的感觉.作为填空压轴题，不仅考查了基础知识、基本技能和基本方法，同时注重解法的多样性与灵活性，注重向量和三角的综合运算，突出了对数学思想和数学方法的考查，集中体现了逻辑推理、数学运算、直观想象等数学核心素养，是难得一见的好题.

3 思路分析及解法赏析

3.1 思路分析

求解4a+c的最小值，关键是利用题目条件建立a,c之间的关系式.解三角形问题一般可借助正弦定理、余弦定理或三角形的性质建立a,c的关系式，也可通过向量建立a,c的关系式，然后借助函数或基本不等式求解.

3.2 解法赏析

在△ABD中，由正弦定理可得

即

在△BDC中，同理可得

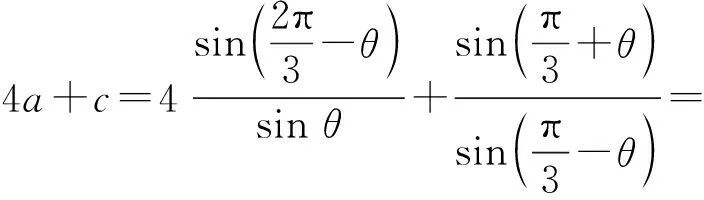
解法2(利用余弦定理)在△ABD中，由余弦定理可得

|AD|2=c2+1-c,

在△BDC中，同理可得

|DC|2=a2+1-a,

由角平分线定理可知

因此

化简可得

(a-c)(a+c)=ac(a-c).

当a=c时，由|BD|=1，可得a=c=2，此时

4a+c=10,

当a≠c时，a+c=ac,即

则

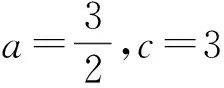
综上所述,4a+c的最小值是9.

解法3(利用面积公式)由题意可知

S△ABC=S△ABD+S△BDC，

即

化简可得

a+c=ac，

即

以下解法同上.

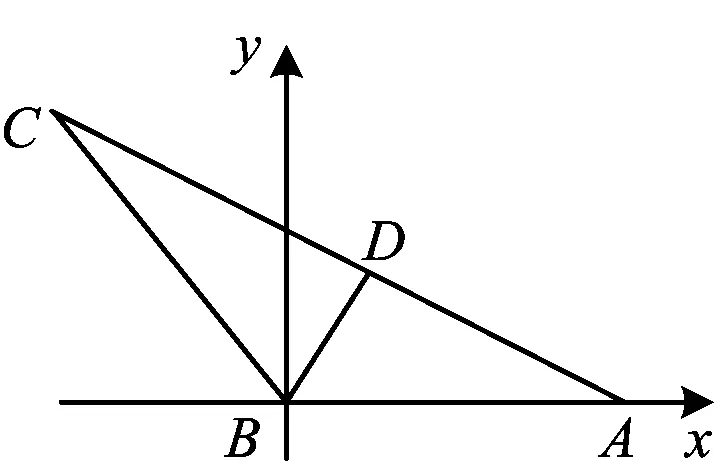
图2

化简可得

a+c=ac，

即

以下解法同上.

解法5(利用基底法)由角平分线定理可知

即

蕉城区水利风景区内未建立导览系统和导览路径，未配有向导解说员。解说牌、印刷品等解说媒体数量较少，存在特色不明显，内容简单，满足不了游客需求，不能向游客展示当地独特的水科技，水文化和民族民俗文化。

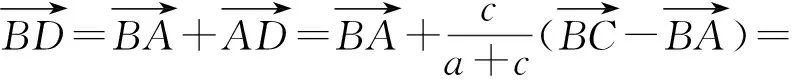
所以

化简得

(a+c)2=a2c2，

即

以下解法同上.

4 教学启示

1)在教学中应注重培养学生的数学运算能力.

对于解法1和解法2,大部分学生都望而却步，主要原因是数学运算不过关，因此在平时教学中应注重数学运算能力的培养.数学运算主要表现为：理解运算对象、掌握运算法则、探究运算思路、求得运算结果等，通过数学运算促进数学思维发展，形成规范化思考问题的习惯，教师绝不能越俎代庖，思路代替不了运算.

2)在教学中应重视知识的生成过程，注意对问题本质的探究.

以上可以看出，作为压轴题，它所涉及的知识大都是多元的，面对多元的基础知识及其相互联系，靠死记硬背肯定不行.在平时的教学中，教师要重视知识的生成过程，帮助学生建立和领会知识体系的网络结构，让学生领略和体会主干知识的常见交会处，教学中要培养学生对知识和问题的本质进行研究的习惯.

3)在教学中应加强数学思想方法的渗透.

解法4和解法5借助向量求解，体现了数形结合的思想.但由于对数学思想方法生疏，考生不易想到，因此，教师应有意识地在传授知识的同时，帮助学生揭示相关的学科思想方法，使他们在获得知识的过程中同步地形成相应学科的思想方法，并自觉地应用这些思想方法来解决问题.