不同浪向下管道下水过程中托管架的动力学分析

张大朋，陈登硕，白 勇，刘松华，朱克强

1.浙江大学建工学院，浙江杭州 310058

2.南方科技大学海洋科学与工程系，广东深圳 518055

3.宁波大学海运学院，浙江宁波315211

对海洋油气能源的开发，尤其是深海中的能源开发，需要结合铺管船及具体海况选择合适的铺管方法，在这些铺管方法中S形铺管法因具备众多优点已成为目前深水管道铺设时经常使用的方法，铺管船托管架在管道下水的过程中起着承受管道荷载并引导管道下水的作用，外界环境载荷会使管道产生剧烈的响应，也使得支撑管道的托管架承受的载荷变得十分复杂，从而使其产生诸如疲劳等各种各样的力学问题。

迄今为止，国内外相关学者对托管架从数值分析和模型试验两方面进行了研究。但大部分方法局限于研究托管架和管道之间的静力分析，没有考虑托管架、管道以及托管架与管道水下部分在外界环境载荷下的运动及这些运动之间的动力耦合作用[1-5]，因此也就无法直接获得托管架在管道下水过程中关键结构如托辊位置变化和托辊与管道间的相互接触力等重要的参数。

本文参考某铺管船托管架具体参数，基于凝集质量法将托管架离散成凝集质量模型，依据工作海域的具体水动力参数将管道运动与托管架运动相互耦合，运用大型水动力分析软件OrcaFlex建立了不同浪向下管道下水过程中托管架的动力学分析模型。结合动力学仿真的计算结果给出了一些指导性的建议，对于保证管道下水安全作业有重要意义，尤其是关于预防管道下水过程中与托管架托辊产生过大的碰撞、研究各个托辊的位置变化和速度变化，进而避免托管架因为承受过大的冲击载荷而发生过大的变形。

1 海洋环境载荷的计算理论

1.1 波浪理论的选择

Dean[6]在文献中指出，大部分情况下应用线性波浪理论都可以得到不错的结果，且随着水深的增加，海浪基本控制方程中的非线性项的影响逐渐降低，因此本文在OrcaFlex的建模过程中选用线性波浪理论。

1.2 托管架的水动力载荷的计算

在管道下水作业时托管架运动的动力学方程为：

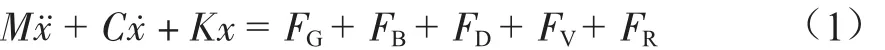
式中：M、C、K分别代表结构的质量、阻尼和刚度；对应的单位分别为 kg、kg/s、kg/s2；FG、FB、FD、FV、FR分别代表重力、浮力、水动力、船体运动引起的惯性力以及管道对托管架的托辊动荷载，kN。

托管架是由中空圆管构成的整体空间桁架。单个中空圆管在波浪作用下受到的波浪力可用莫里森公式表示，托管架所受到的波浪力是其中各个中空圆管受到的波浪力的矢量叠加。

Morison方程的微分形式为：

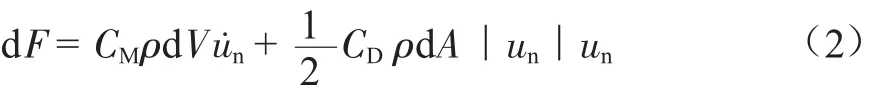
式中：F为受到的波浪力，kN；CD和CM分别代表拖曳力系数和惯性力系数，A为垂直圆柱的迎流截面积，m2；ρ为海水密度，kg/m3；un为流体速度，m/s；V为管道体积，m3。

若垂直圆柱在波浪中自由摇摆，在莫里森方程中必须使用相对速度和相对加速度，微分方程可写为：

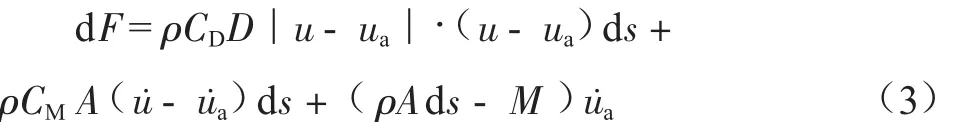
式中：D为管径，m；u为海流速度，m/s；ua为管道运动速度，m/s；s为管道长度，m；A为管道迎流截面积，m2。

而在OrcaFlex中对波浪力的计算正是基于修正后的Morison公式。式（3）即为本文中所采用的扩展型Morison方程，为方便程序处理将其变形为：

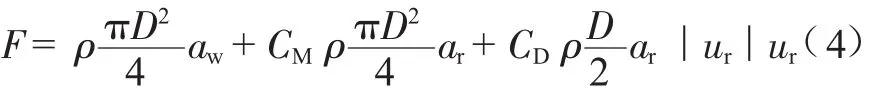
式中：aw为流体惯性坐标系下即相对于海床的加速度，m/s2；ar为流体相对于管道的加速度，m/s2；ur为流体相对于管道的速度，m/s。本文中拖曳力系数CD取为1.2，惯性力系数CM取为2。

基于以上计算理论，将托管架及下水管道离散成凝集质量模型[7-15]，即可进行相关分析计算。

2 在Orca Flex中托管架动力学分析模型的建立

2.1 建模假设

本模型模拟装备有铰接刚性托管架的深水铺管船S型铺管过程，托管架配有托辊并支撑着管道，采用一个恒张力张紧器控制管道的轴向运动。建模中假设：铺设的管道是光滑的并且下水过程中发生弹性应变，不发生塑性应变；为简化模型计算及保证计算的良好收敛性，托管架最上端固定于铺管船海平面位置处。

2.2 托管架及下水管道参数

托管架结构如图1所示，本托管架为3节，曲率半径为125 m，长度为63 m，有10个托辊，托辊间距为6 m，托管架主体由两种不同材质属性的LineTypes单元组成（分别为托管架主框架单元、托管架交叉支撑单元）。下水管道规格为D 250 mm×15 mm，管道长为704 m，托管架上采用滑移管道单元，下水管道采用钢管单元。

图1 托管架结构示意

托管架主框架单元的参数：外径为0.5 m，内径为0.48 m，线密度为7.85 t/m，泊松比为0.293，杨氏模量为212000 MPa，其材质为匀质中空管；托管架交叉支撑单元的参数：外径为0.35 m，内径为0.33 m，线密度为7.85 t/m，泊松比为0.293，杨氏模量为212000 MPa，其材质为匀质中空管。

滑移管道单元的参数：内径为0.25 m，外径为0.28 m，线密度为0.087 t/m，泊松比为0.293，弯曲刚度为16273 kN·m2，轴向刚度为0.1kN，其材质为通用管材（General）；下水管道单元的参数：外径为0.25 m，内径为0.22 m，线密度为7.85 t/m，泊松比为0.293，杨氏模量为212000 MPa，其材质为匀质中空管。

托管架总共由80根管构成，其中作为托管架主框架单元的管为38根，作为托管架交叉支撑单元的管为42根。

在模型中托辊按照从上到下的位置顺序依次命名为托辊1～托辊10，共用10个无属性的6D浮标（即六自由度的浮标）来模拟，每个6D浮标的质量为0.01 t，其三个局部坐标轴的转动惯量均为0，该单元通过与托管架框架的相关节点相连而固结于托管架；与管道的接触是通过接触对的设置实现的，托辊与下水管道之间的接触对设置为：法向接触刚度为1000 kN/m，托辊的接触直径为0.5 m，托辊的长度为3 m，高度为2 m。除最后一个靠近管道下水端的托辊外，其余托辊的形状均为V型，靠近管道下水端的托辊为缓和管道下水的冲击与摩擦，形状设为U型。其中，管道与托辊接触力的计算方法为Fc=kAd，其中k为接触系数，A为管道与托辊的接触面积，m2；d为在接触发生的瞬间沿接触面法线方向管道发生的变形位移，m。

3 外界环境参数及OrcaFlex中模型的建立

自上而下沿着管道长度方向在252.5 m处管道开始与海床发生接触。模型中的环境参数为：水深100 m，海水密度1025 kg/m3，考虑流向为定常流，流速方向不变、大小为0.5 m/s，波高为1 m，周期为8 s，每隔45°取一个浪向，暂不考虑风的作用。建立的模型如图2所示。

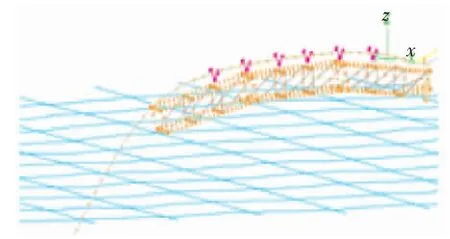
图2 托管架动力学模型示意

3 计算结果

3.1 不同浪向下托辊与管道的接触力

不同浪向下各个托辊与管道的接触力在时域上的分布如图3所示。

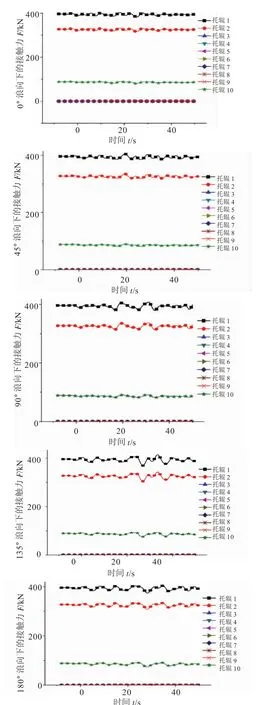
图3 不同浪向下托辊与管道的接触力

从图3可以看出：托辊3、托辊4、托辊5、托辊6、托辊7、托辊8、托辊9在管道下放过程中并未与托辊发生接触；托辊1、托辊2、托辊10始终与管道保持接触，与管道的接触力按照数值大小从大到小的排布顺序为托辊1、托辊2、托辊10，这说明其接触力从海面上到水下沿着托管架的弧度依次递减；同时发现，随着浪向的改变，各个托辊的接触力呈现微幅的波动，这说明浪向的改变对托辊的接触力变化有一定的影响，对比观察0°浪向与180°浪向时托辊的接触力图像发现，逆浪向时托辊的接触力变化要比顺浪向时托辊的接触力变化要大，分析产生这种现象的原因是逆浪向时随着波浪的起伏管道不断随波逐流，使得管道上端与入水端不断与上端的托辊及下端的托辊反复碰撞，进而使得此时接触力幅值发生波动；而在横浪向时，其接触力波动幅度要比斜浪向时波动幅度大；各个浪向下托辊的接触力波动幅度从托管架上端到下端依次减小。

3.2 不同浪向下托管架托辊的位置变化

不同浪向下各个托辊的位置在时域上的图像如图4所示。

从图4可以看出：托辊8、托辊9、托辊10在不同浪向下位置的波动幅度最大；托辊3、托辊4、托辊5、托辊6、托辊7位置的波动幅度也会随着入水深度的增加依次增加；而最顶端的托辊1靠近托管架最上端的固结点且由于其在海面以上波浪对其影响的作用最弱，位置几乎无波动；托辊2的位置仅有微弱波动。这说明越远离海面，托管架上端的固结限制作用越弱，而水下部位波浪力对托管架各个托辊及管道的运动的影响就越剧烈，这也就使得这些部位的托辊的位置变化越明显越剧烈。也就是说，不同位置的托辊在管道下水过程中的位置变化波动幅度是不同的，入水深度越深，托辊位置变化的波动幅度就越大。

3.3 不同浪向下托管架托辊的运动速度变化

不同浪向下各个托辊在时域上的运动速度图像如图5所示。

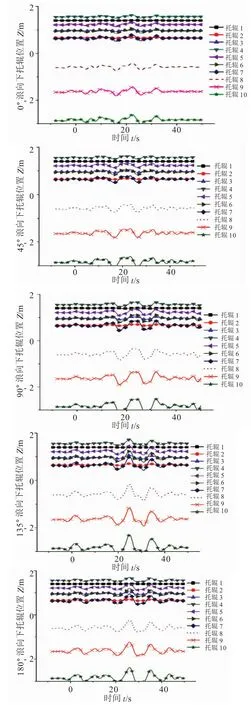
图4 不同浪向下托辊的位置变化

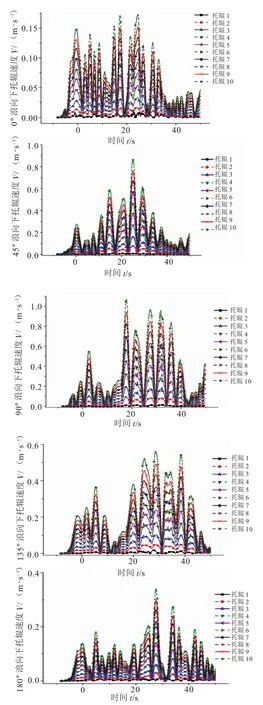
图5 不同浪向下托辊的运动速度变化

从图5可以看出：托辊速度的变化对于浪向的改变较为敏感，不同浪向下各个托辊的最大速度值相差很大。在浪向为0°～90°时，各个托辊的最大速度随着浪向角的增大呈现出先增大后减小的趋势，具体来说，在0°～60°浪向时，各个托辊的最大速度随着浪向角的增大而增大，在60°～90°浪向时，各个托辊的最大速度随着浪向角的增大而减小；在浪向为90°～180°时，各个托辊的最大速度随着浪向角的增大先减小，然后几乎保持不变，具体来说，在浪向为90°～135°时，各个托辊的最大速度随着浪向角的增大而减小，在浪向角为150°～180°时，各个托辊的最大速度随着浪向角的改变几乎保持不变，但在时域上达到最大速度的时刻有所不同；不同浪向作用下，在浪向为60°时各个托辊的最大速度最大；不同浪向作用下，离上端越远的托辊速度越大，托辊10的速度最大。

4 结论

通过观察仿真结果发现：

（1）在与管道发生接触作用的托辊上，其接触力从海面上到水下沿着托管架的弧线依次递减，逆浪向时接触力变化要比顺浪向时剧烈。

（2）越远离海面托管架上端的固定限制作用越弱，而水下部位波浪力对托管架各个托辊及管道的运动的影响就越剧烈，这也就使得这些部位的托辊的位置变化越明显越剧烈；不同位置的托辊在管道下水过程中的位置变化波动幅度不同，入水深度越深，托辊位置变化的波动幅度就越大。

（3）不同浪向下各个托辊在时域上的速度图像表明：托辊速度的变化对于浪向的改变较为敏感，不同浪向下各个托辊的最大速度值相差很大；不同浪向作用下，离上端越远的托辊速度越大。

总的来说，依据管道与托管架托辊之间的接触力大小可以确定导管架与管道之间的相互接触状况，进而可考虑管道与托管架之间的磨损情况；托辊位置及速度的变化可以显示不同位置的托辊的位移与形态，进而可以依据不同时刻各个托辊的位置总体上判断此时托管架的空间构型；同时，依据不同位置托辊速度的变化情况可以得到托管架不同位置的加速度变化情况，对加速度变化较快的部位其强度及疲劳寿命有着较高的要求，在具体工程实践中应注意对这些部位采取相关措施。而依据托辊对于浪向改变的敏感性这一特点，在具体工程实践中可选择合适的浪向进行铺管作业，以最大程度保证铺管作业安全。