基于ALE法分析桩靴插桩对邻近基桩承载力的影响

2018-09-06张海洋

石油工程建设 2018年4期

肖辉，张海洋，万军，关湃

1.中海石油（中国）有限公司天津分公司，天津 300459

2.天津大学水利工程仿真与安全国家重点实验室，天津 300072

自升式钻井平台通常在固定式平台附近进行作业，因此桩靴在贯入过程中不可避免地对邻近桩基础产生影响[1]。WU等[2]在有机玻璃模型槽内开展了砂性土条件下的1g模型试验，研究桩靴贯入对邻近基桩桩顶位移的影响。离心模型试验也是目前研究桩靴插拔对邻近基桩影响的主要手段之一，但由于离心模型试验费用高昂且试验条件限制较多，目前仅有的一系列离心试验结果[3-6]并不能对各参数提供完整的分析。

在采用数值方法研究桩靴贯入过程时，需要采用大变形算法，THO等[7]首先引入CEL法解决网格的大变形问题；在研究桩靴贯入过程对邻近基桩变形的影响时，也有学者提出了改进的CEL计算方法[8-9]，此方法中欧拉土体和拉格朗日土体并存，可以有效地嵌固桩底，修正桩身变形问题，但欧拉土体和拉格朗日土体的占比对基桩承载力的计算结果有一定程度的影响，因此在计算基桩承载力过程中如何确定不同土体的占比仍有待进一步研究；一些学者开发了mesh-to-mesh网格重划分算法来研究桩靴贯入对邻近基桩的影响，但此算法未能应用于三维模型，从而产生了很多局限性[10]；而桩靴贯入过程对邻近基桩极限承载力问题的研究报道多是基于静力算法和拟静力算法[11]，此方法无法完全模拟出桩靴的整个贯入过程，计算结果的合理性有待进一步研究。综上所述，采用常规方法研究桩靴贯入过程对邻近基桩承载力的影响均存在诸多限制。本文提出采用ALE网格重划分技术研究桩靴贯入过程对邻近基桩承载力的影响，可以完整分析桩靴的贯入过程，其模型中均为拉格朗日土体，不存在CEL算法中改进不同土体占比的问题，研究此问题较上述方法更加合理。

1 ALE模型的建立

1.1 ALE方法简介

ALE（Arbitrary Lagrangian-Eulerian）自适应网格技术通常被称为任意的欧拉-拉格朗日分析方法，该技术[12]结合了纯拉格朗日分析方法和纯欧拉分析方法，是一种分析网格大变形问题的数值计算方法。ALE自适应网格技术不同于动力算法中的纯欧拉分析技术。纯欧拉分析技术允许在一个网格中同时存在多种材料和空穴，可以更有效地处理分析极端变形情况。相比之下，ALE网格只允许单一材料完全填充，这种设定使材料的变形受限于网格的变形情况，但是它可以更精确地定义材料边界条件和更复杂的接触条件。

1.2 相关模型参数

为节省计算资源，采用四分之一模型进行计算。其中桩靴直径dspu=6 m，土体半径Rsoil=27.5 m，土体高度Hsoil=37 m；基桩直径dpile=1.26 m，基桩长度Hpile=30 m，桩头出土高度Hhead=3 m，基桩边缘与桩靴边缘的距离为L=6 m，具体见图1。

2 基桩承载力的动力算法及验证

图1 模型装配示意

在采用动力算法计算基桩承载力的过程中，网格加密区尺寸、网格尺寸和加载速度对计算结果均有不同程度的影响。将对上述三个因素进行灵敏度分析以确定最优计算结果，并将其与静力算法、API规范[13]计算方法所得结果进行比较，以验证其正确性。在分析过程中，黏土有效重度γclay=6 kN/m3，泊松比υ=0.48，采用不排水总应力分析方法，假定黏土的不排水抗剪强度不随深度发生改变，即为均值土，不排水抗剪强度su=20 kPa。桩-土之间的法向接触行为视为“硬”接触，切向接触行为的摩擦系数取fpile=0.364；因为土体弹性模量对基桩竖向极限承载力的影响较小，在此分析中假定Esoil=100 su。

2.1 网格加密区尺寸

图1中的Dpile为网格加密区的直径。因为模型尺寸关系，当该直径与基桩直径之比，即Dpile/dpile>4或者Dpile/dpile<2时，会划分出极端扭曲的网格，因此仅针对2≤Dpile/dpile≤4的情况进行灵敏度分析，具体计算结果如图2所示。

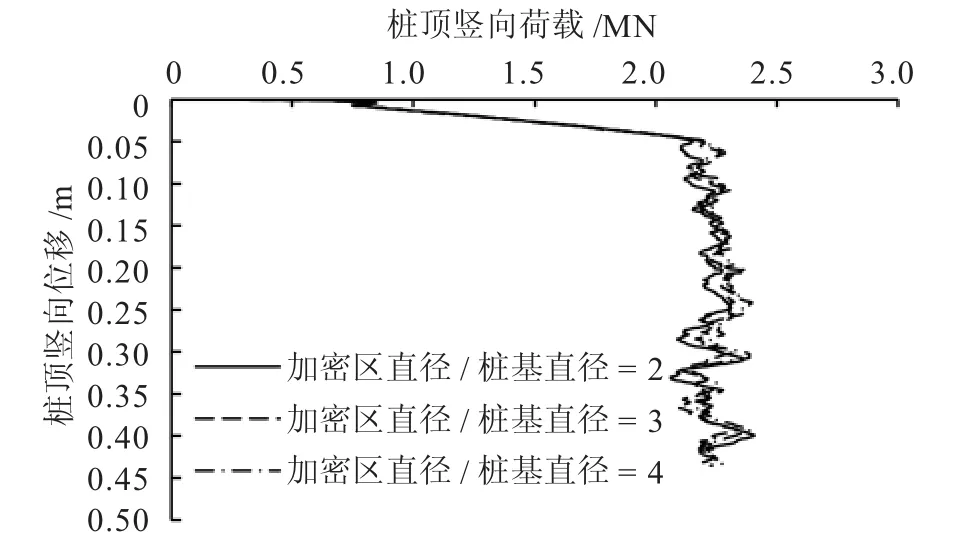
图2 网格加密区尺寸的灵敏度分析

由图2可以看出，网格加密区的尺寸对计算结果几乎没有影响，为了节省计算资源，在采用动力算法计算基桩承载力时，网格加密区直径建议取2倍基桩直径，即Dpile/dpile=2。

2.2 网格尺寸

在Dpile/dpile=2条件下对网格加密区内的网格尺寸进行灵敏度分析，具体分析基桩径向网格个数nr为4≤nr≤20的情况，计算结果如图3所示。

图3 网格加密区径向网格尺寸的灵敏度分析

由图3可以看出，网格加密区的径向网格尺寸对计算结果存在一定程度的影响。但径向网格个数大于8后，对计算结果的影响基本可以忽略。因此在采用动力算法计算基桩承载力时，基桩的径向网格个数建议设置为8个，即nr=8。在此条件下，对基桩周长向网格尺寸进行灵敏度分析，分析基桩周长向网格个数2≤nl≤6的情况，具体计算结果见图4。

图4 网格加密区周长向网格尺寸的灵敏度分析

由图4可以看出，与径向网格尺寸的规律性相似，网格加密区周长向网格尺寸对计算结果存在一定程度的影响。但网格个数大于4后，对计算结果的影响基本可以忽略。因此采用动力算法计算基桩承载力时，周长向网格个数建议设置为4个，即nl=4。

2.3 加载速度

在上文确定的条件下对桩顶的荷载加载速度v进行灵敏度分析，结果见图5。

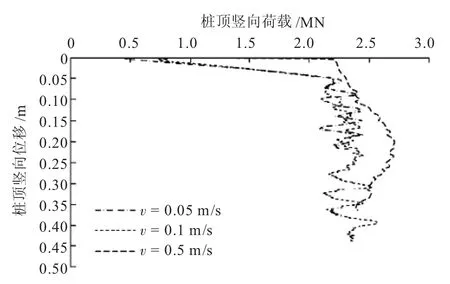
图5 加载速度的灵敏度分析

由图5可以看出，当加载速度过大时会对计算结果产生一定程度的影响。经过分析后发现，当加载速度小于0.1 m/s时，可以得到相对稳定的计算结果。因此计算基桩竖向承载力的过程中，桩顶荷载的加载速度建议设置为0.1 m/s，即v=0.1 m/s。

为确保动力算法计算基桩承载力的正确性，采用静力算法和API规范计算方法对相同型号基桩的承载力进行计算，并将计算结果与动力算法计算结果进行对比，对比结果如图6所示。

由图6可以看出，三种计算方法得到基桩承载力计算结果基本一致。基于上述分析可以认为，采用动力算法得到的基桩承载力计算结果的准确性可以得到保证。

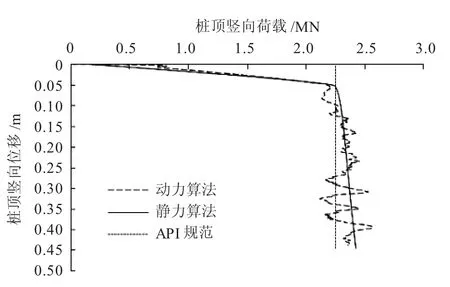
图6 动力算法与静力算法计算基桩承载力结果的对比

3 ALE方法计算桩靴最大贯入深度的影响因素分析

利用ALE算法分析桩靴贯入过程时，土体不排水抗剪强度、ALE边界尺寸、网格尺寸和土体弹性模量均对计算过程中桩靴的最大贯入深度有影响。本节分析在周边无桩条件下，上述因素对桩靴最大贯入深度的影响，并确定最终算法。

3.1 土体不排水抗剪强度

本节将研究土体不排水抗剪强度su对桩靴最大贯入深度D的影响，具体分析2 kPa≤su≤20 kPa的工况，计算结果见表1。

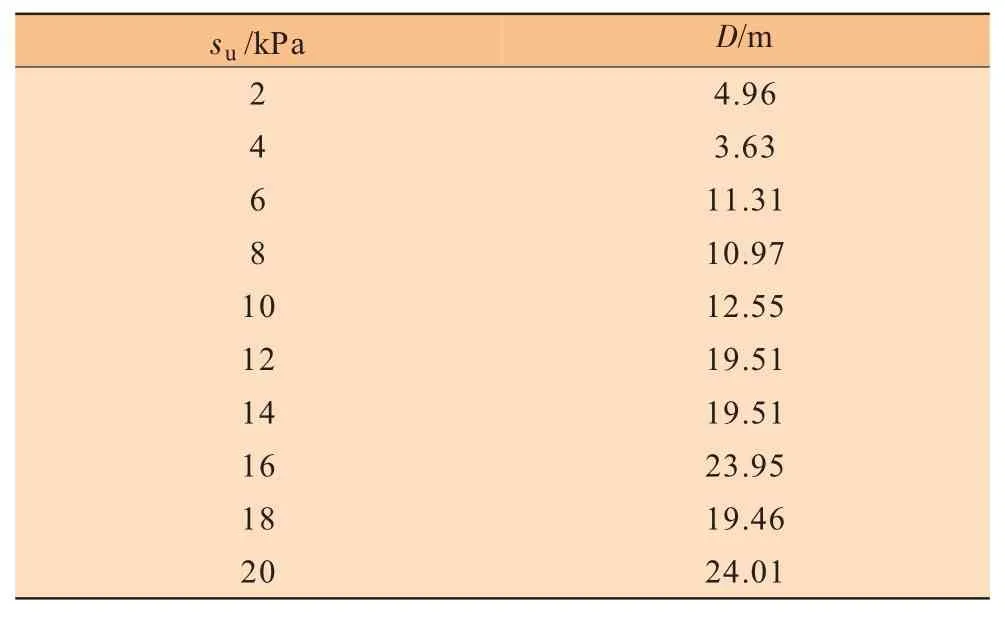
表1 桩靴最大贯入深度随土体强度的变化情况

由表1可以得到，随着土体不排水抗剪强度的增加，桩靴的最大贯入深度基本上呈线性增加。分析认为，随着土体不排水抗剪强度的增加，桩靴贯入过程中土体的变形，尤其是土体回流变形相对较小，ALE网格重划分算法更易处理，因此在计算过程中，桩靴能贯入至更深的深度。

3.2 ALE边界尺寸

由上述分析可以得到，在计算过程中当土体强度相对较高时，桩靴的贯入深度已经可以得到保证。为提高在土体强度较低时的桩靴贯入深度，对su=2 kPa的情况进行分析。首先对模型中ALE区域的尺寸进行研究，具体研究9 m≤RALE≤15 m的工况，结果见表2。

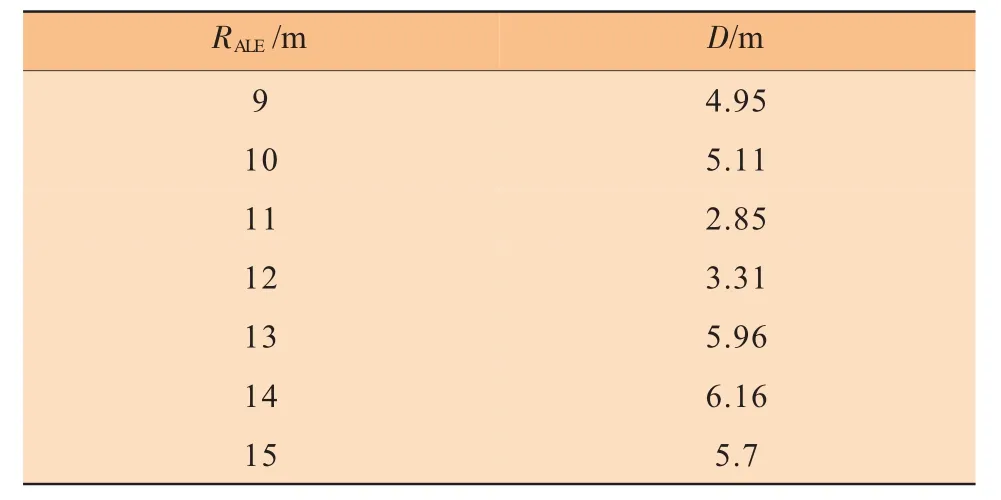
表2 桩靴最大贯入深度随AL E区域半径的变化情况

由表2可以得到，整体而言随着ALE区域半径的增加，桩靴的最大贯入深度得到了提高，但两者关系并不明显，影响程度有限。相较于土体的不排水抗剪强度而言，通过增加ALE区域半径的方法来提升桩靴最大贯入深度效率不高。

3.3 网格尺寸

ALE网格重划分算法对于初始网格的质量有较高的要求，因此有必要研究ALE区域内网格尺寸对于计算过程中桩靴最大贯入深度的影响。首先研究ALE区域内径向网格数量对桩靴最大贯入深度的影响，在上述分析的基础上研究16≤nR≤80的情况，结果见表3。

表3 桩靴最大贯入深度随AL E区域内径向网格数量的变化情况

从表3可以得到，桩靴的最大贯入深度随着径向网格数量的增加有一定程度的增加，但当网格数量达到一定数值后，再增加网格数量对于贯入深度的提高并不明显。因此在这种情况下，ALE区域内径向网格的数量建议设置为32个，即nR=32。

在确定ALE区域内径向网格数量后，需要对ALE区域内周长向网格的数量进行分析。具体研究ALE区域周长向网格4≤nL≤20的情况，结果见表4。

表4 桩靴最大贯入深度随AL E区域内周长向网格数量的变化情况

从表4可以看出与ALE区域径向网格数量对计算过程中桩靴最大贯入深度的影响规律相似，周长向网格数量对桩靴最大贯入深度有一定程度的影响，当网格数量增大到一定程度后，再增加网格数量对于贯入深度的提高并不明显。因此在这种情况下，ALE区域内周长向网格的数量建议设置为12个，即nL=12。

3.4 土体弹性模量

土体弹性模量对桩靴贯入深度同样有影响，因此需要对土体的弹性模量进行分析。具体研究100≤E/su≤1000的情况，结果见表5。

表5 桩靴最大贯入深度随土体弹性模量的变化

由表5可以得到，土体弹性模量对计算过程中桩靴的最大贯入深度有一定程度的影响。但随着土体弹性模量的增加，桩靴最大贯入深度的变化情况并没有明显的规律性，无法判断土体弹性模量与桩靴最大贯入深度之间的关系，因此每次采用ALE网格重划分技术进行桩靴贯入分析之前，应对土体的弹性模量进行充分分析后，再进行后续计算。

4 桩靴贯入对邻近基桩的影响分析

在上述研究的基础上，分析桩靴贯入过程对不同间距邻近基桩的影响，并研究其规律性。具体研究工况为：基桩和桩靴的间距与桩靴直径比L/dspu=0.5、0.75、1以及无桩靴贯入时基桩的极限承载力情况，计算结果如图7所示。

图7 基桩承载力随L/dspu的变化情况

由图7可以看出，单就桩靴贯入过程而言，对邻近基桩承载力有相对积极的影响，但随间距的增加，影响衰减相对较快。在L/dspu=0.5时，极限承载力上升了9.92%；在L/dspu=0.75时，极限承载力上升了3.34%；在L/dspu=1.0时，极限承载力仅上升了1.43%。因此可以认为，自升式钻井平台工作期间，在不破坏基桩本身结构的前提下，不会降低邻近基桩的极限承载能力。

ALE网格重划分技术的模拟结果中，位移值不是实际位移，因此没有参考意义，但是等效塑性应变值为真实值。图8列举了L/dspu=0.5情况下，桩靴贯入0、5、10、15 m时，土体的等效塑性应变云图。

从图8可以看出，在桩靴贯入过程中的土体影响区域随桩靴贯入深度的增加而有所增加，但当桩靴贯入至10 m左右时，影响半径基本稳定在11.5 m左右，影响区域边缘至桩靴边缘的水平距离为5.5 m，小于0.5倍桩靴直径。因此桩靴贯入过程对土体的影响范围相对较小，可以认为此过程几乎不影响距桩靴边缘0.5倍直径以外的基桩承载力，与上文所得基桩承载力变化情况的计算结果基本一致，因此可以认为此结论具有可靠性。