综合实践课的教学素材来源及创造性运用——以“周长与面积问题”的教学为例

江苏徐州市云兴小学（221000）

为了让学生经历活动本身，认识到“周长相等，面积有大小”以及“周长恒定时，所围的图形中正方形面积最大”等本质问题，在进行了两轮试教后，我们对“周长与面积问题”这一课进行了第三次教研活动。

一、教学示例

【第一个环节】

师（边说边演示课件：如图1①，用5条线段围成图形，随即让学生指出周长与面积；如图1②，将上端两线段向内凹，让学生再次指出周长和面积）：你有什么发现？

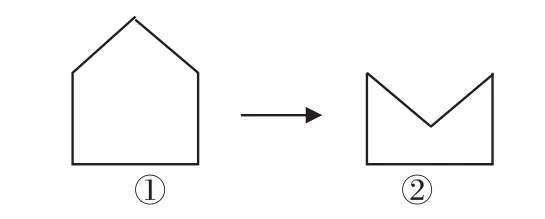
图1

生（齐）：周长不变，面积缩小了。

师：为什么？

生1：原来饱满的图形凹陷了。

生2：原来的图形中有两条邻边发生了相对位移，整个图形变形了。

生3：整个图形由舒张变成收缩，但是由于每条边的长度没有变，因此周长不变。

师：请通过观察，结合对周长和面积概念的理解，判断这两个量的变化情况。（板书（主标题）：周长不变，面积有变）

师（板书探究提示语：变大还是变小？什么情况下变大？什么情况下变小？……）：今天就来学习周长与面积的关系。（板书总课题：周长与面积）

【第二个环节】

师（质疑）：我们的猜测对吗？

（学生掏出12根小棒在方格纸上拼搭：先围一个正方形，分别测算出周长和面积。不少学生用12根小棒围成一个正方形，如图2所示）

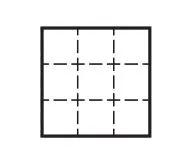
图2

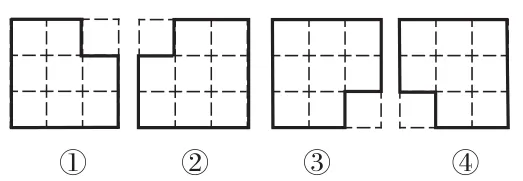
图3

（让学生以图2为原型，移动2根小棒将图2中的9个小方格变为8格。学生交流后，教师出示图3①，并经过旋转位移得到其余三个图形，如图3②③④所示）

师：能不能变成7格？

（学生操作、交流、汇报展示后，教师出示对应图形）

师：能否将其变成6格、5格，并且画出来？

师（学生在展示台上交流后，教师依次贴出相应模型（图略），并让学生多角度观察）：周长相等的图形，面积一定相等吗？

生1：周长一样的图形，有时面积会更小。

师：理由是什么？

生1：凹进去了一部分。

生2：周长相等，有时面积也相等。

师：理由是什么？

生2：凹进去的格数相同。

师：概括起来应该怎么说？

生（齐）：面积未必相等。（学生通过数学活动，检验出猜想的部分正确）

师：还有无其他发现？

生3：凹进越多，面积越小，反之越大；没有凹的就是正方形，此时面积最大……

【第三个环节】

师：周长相等，要使面积最大化，图形一定要饱满，像长方形、正方形。（引导学生用16根小棒拼接成矩形，然后绘制到方格纸上，再观察分析）

（学生用小棒围成了如图4所示的四个矩形，并得出：周长相等的矩形中，长与宽差距越小，面积就越大；当长与宽差距为0，即围成正方形时，面积最大）

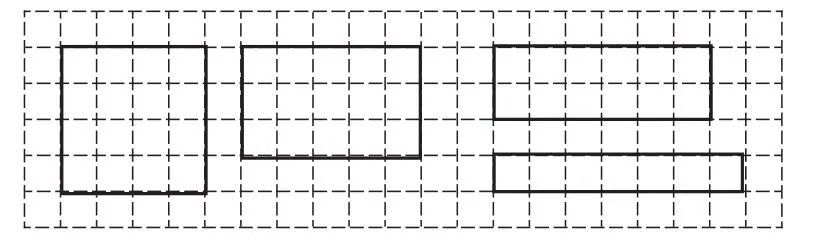
图4

二、数学综合实践的素材来源

小学数学活动以“综合实践”为主。“综合与实践”的素材来源有如下两方面：

（1）源于教材。“综合与实践”课程内容一般在单元总结后面，旨在让学生综合运用所学数学知识解决问题。教材中的“综合与实践”内容没有配套练习，因此需要教师到网络上或者优质教辅上寻找相关的习题素材，进行适当改编改造，增加趣味性和科学性，变成可操作的游戏题或活动题，对学生进行针对性的训练，让学生学会用实践验证知识，寻求答案。

（2）源于教师原创。如教学了“统计与概率”后，教师要求学生调查各自家庭的家电信息，如各种电器的价格、技术参数、功率、外观设计数据等，让学生经历数据收集、整理、展示的过程。此类作业，能让学生在亲自动手的过程中体验到统计的方法步骤以及指导思想。不仅如此，学生学会分析数据后，也能评估各种家电的性能，学会保养、爱护、维修，还会考虑如何节能。

综合实践课有别于具体知识的传授灌输。因此，教学综合实践课时，不妨采用杜威的“五步教学法”（情境→设问→猜想→方式→检验）。因为综合实践课的宗旨就是要在实践中出真知，让学生学会用实验结果说话，但是实验不是片面地追求好玩，操作要有科学性和教育理论的支撑。发现问题、提出问题、建立实验模型有时远远比实验过程本身更重要。

根据小学生的心理特征，对于“情境→设问→猜想→方式→检验”这个过程，前三步可以合并，方式与检验也可以交替开展。因此，可将综合实践课的基本流程改编为“情境/设问/猜想→方式/检验（结论）”，可以将发现问题、提出问题和做出猜想三大环节进行整合，让学生置身于问题情境中，以问题为导向，所有的质疑与推理活动都紧密围绕在中心问题周围，让后续的探究活动扎根于深厚的理论土壤中。

三、创造性运用的关键

小学数学综合实践课，如果原原本本照抄“五步教学法”，时间不够，也难以保障收效。因此，教师要学会创造性地运用。

1.选择问题应恰当

在本课中，教师设计了一系列情境：用课件演示5条线段拼接成的形形色色的图形，学生观察分析得知“调整一些线段后，周长相等，面积缩小；两条线段变成拱形后，面积变大；周长相等，面积可能变大也可能变小……”，就会产生疑虑“周长相等的图形，面积怎么会不等？”并顺着这个疑虑一路探索下去。

2.设计好活动过程

本课中，活动的前两个环节，让学生重点经历“情境/问题/假设→检验”的数学活动，并感悟设想与检验的重要性，得出“周长相等，面积未必相等”的结论。

为了使学生的检验过程得到有序推进，教师分三步导引：先展示8格图（如图2、图3），示范；然后移动小棒得到7格图；最后画出6格图和5格图。围小棒、移小棒、画小棒，在有限的时间里开展丰富多样的活动，能大幅缩减活动时间。

操作完毕后，教师要求学生多角度观察，并进行归纳总结，得到“周长相等，面积未必相等”的观点。这样一来，一方面，实践出真知；另一方面，由于学生对真理的感知不一，在解读上难免有差异，而交流和分享有助于达成共识。

另外，数学基本活动经验需要在具体操作、实际考察和认真思考后才能形成，这些经验会为学生的终身学习打下基础，教师对学生数学基本活动经验的培养要加以重视。