立足全国卷导向 优化高中数学课堂教学设计

陈伟长

（龙海市实验中学，福建 漳州 363100）

2016年10月，教育部考试中心主任姜钢在《中国教育报》撰文指出：“高考改革——探索构建‘一体、四层、四翼’的评价体系。”其中“四翼”是指全国卷的题目设置主要考查基础教育过程中学生所掌握知识的“基础性、综合性、应用性、创新性”。［1］通过这四个方面的考查要求，回答了高考“怎么考”的问题。俗话说得好：战怎么打，兵就要怎么练。要应对“基础性、综合性、应用性、创新性”这四个方面的知识考查，高中教师必须通过三年的高中课堂教学及课堂外知识跟踪指导，帮助学生丰富、完善基础教育知识储备中的基础性、通用性知识，这些知识是学生高考中应对综合性、应用性、创新性知识考查必须要具备的，同时也是学生今后进入高校深造以及终身学习所必备的。

一、立足基础性知识进行教学设计

基础性知识是指中小学课程标准中所要求的知识。它是学生进入高校后继续深造或进入社会继续学习所应具备的基础性知识。通过这些知识的学习，可以让学生的基础性知识的结构更加全面合理、知识应用能力更加扎实灵活、数学素养不断提高。全国卷很注重基础性知识即通用性知识考察，一题往往涉及众多知识点。比如2017理科数学全国卷1第11题：设xyz为正数，且2x=3y=5z，则

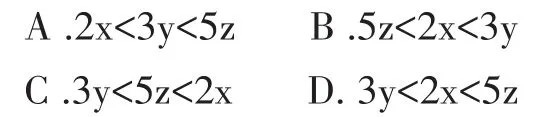
［分析］（1）直观想象：要比较 2x，3y，5z的大小，不妨先求x、y、z，故设2x=3y=5z=t。

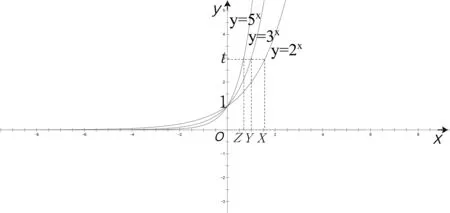
图1

（3）直观想象（数形结合）：此时要确定2x-3y的符号，必然要得到 t的范围。故设函数 y=2x，y=3x，y=5x，根据a＞1时，a越大图像越靠近坐标轴，如图1由2x=3y=5z=t且xyz为正数，知t＞1，所以 lgt＞0，又因为lg9-lg8＞0且lg2·lg3＞0则2x-3y＞0即2x＞3y.同理可证5z＞2x.故选D.

此题考查内容涉及初等函数模块中指数式对数式互换、对数运算法则、指数对数函数图像与性质，以及做差比较法。题目短小精悍，以能力立意，还渗透对高中生逻辑推理能力、直观想象能力、数学运算能力等核心素养的考查。因此，高中数学各阶段的复习教学都要关注知识点覆盖面，立足基础性知识进行教学设计。

二、立足知识综合性进行教学设计

知识综合性是指同一学科内相同知识模块或不同知识模块间知识点的有机结合以及不同学科间知识的交叉渗透。“综合性考查”目的是考查学生是否善于透过事物的表面，从中进行数学抽象，利用学过的数学知识解决问题的能力。这就要求教师要立足知识综合性进行教学设计，慢慢地培养学生多角度观察问题、思考问题，发现、分析问题和解决问题的综合能力。

比如2017理科数学全国1卷第12题就是一道综合性很强的题目。数列中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推。可知第一项1个数，第二项2个数，第三项3个数，第四项4个数…第n项n个数且这n个数的和为2n-1，因此，前n项一共有个数，求和为2n+1-n-2。从题目已知条件N＞100，知n≥14。根据（1）得出的结论分析，前14项有105个数，求和为215-16，故当N=110时，其和是215-16＋25-1=215-17，结果是奇数，不满足2的整数幂（偶数）。同理，当n=20，25时都不符合，当n=29时有435个数，和为230-31，故当N=440时，其和是230-31＋25-1=230，符合题意，所以选A。

此题把不同模块的知识点进行整合应用，以现实生活中的热点问题为背景，将软件激活码的获取抽象为数学问题——幂、不等式运算和数列求和，从中考察学生对数列求和等基础性知识掌握情况，以及进行数据分析和处理的综合能力。因此，在教学过程中，对于综合性较强的题目，不能放弃，应当鼓励学生不要有畏难情绪，要认真审题，寻找问题解决的突破口。比如此题的突破口是“其中第一项是20，接下来的两项是 20，21，再接下来的三项是 20，21，22，依此类推”。

三、立足知识应用性进行教学设计

应用问题主要考察学生是否善于应用所学的知识的能力，要求学生能透过问题的表象，认清问题中所蕴含的数学知识，做到学以致用。

比如2017文科全国Ⅰ卷第19题，以随机抽样——系统抽样构建样本，设制题问。表面上是考查统计学中均值、方差在解决实际问题中的应用，实际上是要考查学生在数据分析、数学运算、逻辑推理（类比）方面的核心素养。具体分析如下：

根据题意，样本数据有 (xi,yi)(i=1,2,···,n)(xi,i)(i=1,2,···,16),故 1，2，3，…，16的平均数为 8.5，即y¯=8.5，所 以 (xi,i)(i=1,2,···,16) 的 相 关 系 数 r=对照题目中条件可知分子为-2.75，分母为4×0.212×18.439，求得r≈-0.176，则|r|＜0.25，据题设可判断这一天的零件尺寸不会因生产的推进而发生系统性变大或变小。数据分析：x¯-3s=9.97-3×0.212=9.334，x¯+3s=9.97+3×0.212=10.636，第13个零件的尺寸为9.22，9.22＜9.334，所以从这一天抽检的结果看，检验员需对当天的生产过程进行检查。剔掉9.22，这条生产线当天生产的零件尺寸的均值为根据 s=

此题表面看起来简单，但整道题目有390个字，要求学生能快速阅读并准确审题，因此，教学中可尝试让学生通过书信阅读训练他们的审题速度。比如让学生为自己设限，一分钟、两分钟能理解几个字，不断挑战以求进步。魏书生在《一分钟竞赛》文中指出：经常开展这样的竞赛，可以增强学生的注意力，提高学生的学习积极性。［2］同时，教师对于教学进程中碰到的知识模块应用，比如函数模型应用、导数综合应用、解三角形应用、不等式（线性规划）应用、统计与概率应用等，不能因题目长、运算烦而简单应付，甚至跳过不讲。相反，教师要更加精心设计，多选择一些与实际生活热点问题为背景的题目，让学生练习，然后讲解，从平时点点滴滴中，培养学生不畏难、不畏烦，善于观察问题、主动灵活地应用所学知识分析和解决实际问题的能力。

四、立足知识创新性进行教学设计

创新性是指学生能综合应用所学的基础性知识，从不同方向、角度，有批判性、创新性地解决问题的能力。高中阶段对学生的数学素养培养，最终就是要培养学生的创造能力，让学生拥有创新性思维。人们在进行创造性思维时，既需要分析，也需要综合；既需要发散，也需要集中，且创造性更多地是表现在发散性上，全国卷就很注重这方面考查。比如2017理科全国卷1第17题：△ABC的内角A，B，C的对边分别为a，b，c，已知△ABC的面积为

（1）求sinBsinC；

（2）若6cosBcosC=1，a=3，求△ABC的周长。

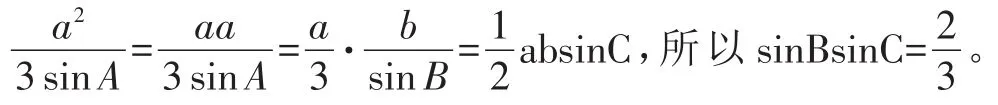
此题得分率很低，题目中没有已知的角、边，第一步考生只能根据题目中的已知量和所求的量进行联想，利用正弦定理、正弦面积公式构建等式。第二步考生同样要通过联想和想象，利用第一步所得结论进行求角。这种建立在基础性、综合性、应用性能力较强基础上的直观想象，可间接反映出学生的创新意识。

综上所述，教师在平时的教学设计中要认真研究以往全国卷的试题模式，坚持从“基础性、综合性、应用性、创新性”四个方面考虑问题，既要做到“坚持能力立意，关注通性通法，淡化解题技巧”［3］，更要坚持“素养立意”，有目的、有计划、循序渐进地帮助学生通过自身的解题实践，慢慢地完善知识系统。