高中数学教师解题的思维固化及其对策——一道教师技能大赛试题引发的思考

廖金祥傅 磊 王成焱

（1.厦门第二中学，福建 厦门 361009；2.厦门双十中学，福建 厦门 361009）

2018年5月13日,厦门市举行了教师技能大赛,其中高中数学组有一项目是“解题析题”。各个学校的优秀选手参加了该项比赛,并在比赛中展示了个人风采，从不同的角度提供了丰富的解法。这次比赛在新课程、新课标、新高考的“三新”背景下举行，参赛的教师在解题能力和析题能力上得到了很好的锻炼，提升了教师自身的数学核心素养，也有利于促进教师培养学生的数学核心素养。

一、教师技能赛试题呈现

等边三角形ABC的边长为1，点P在ΔABC外接圆的劣弧AB上，求SΔPAB+SΔPBC的最大值。

本题是最值问题，常用的解题工具有导数、三角有界性、不等式等；相关的基础知识是函数、三角和解析几何等；基本思想方法是数形结合、函数与方程思想、化归与转化思想等。

二、选手主要方法

（1）三角函数法

由于点P的运动，才导致面积和的变化，在圆中点P的运动可以转化为角的变化，进而将面积最大值的问题转化为三角函数最大值的问题。

（2）解析几何法

通过建立平面直角坐标系，将面积和最大的几何问题转化为代数问题（图1）。以线段AB所在直线为x轴，线段AB中垂线为y轴建立如

图所示的平面直角坐标系，可得

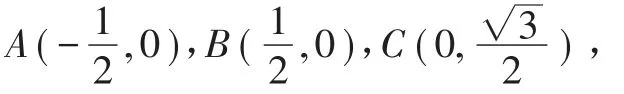
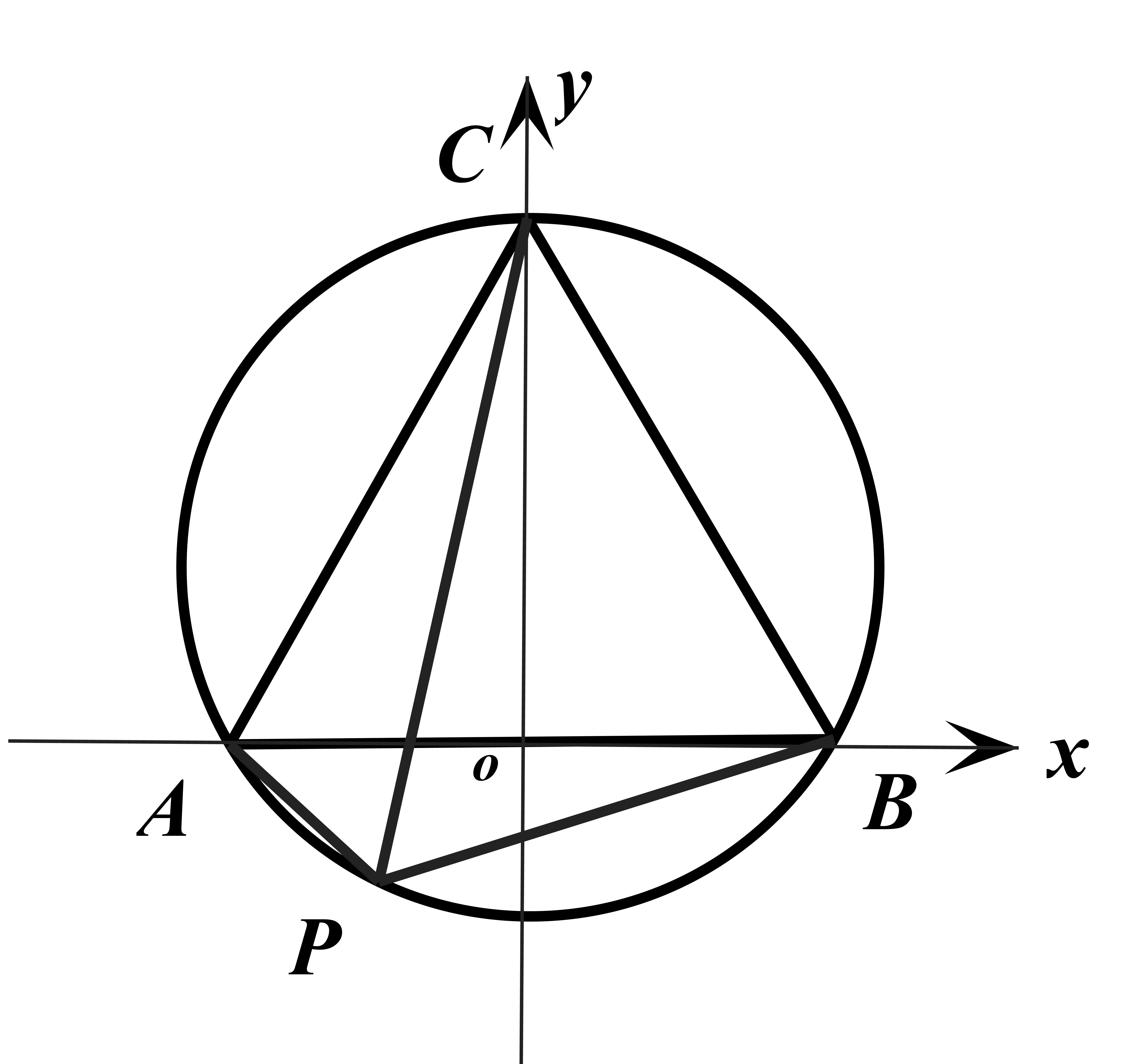
图1

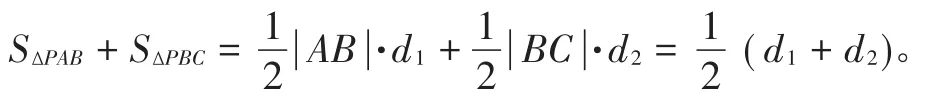
设P(x0,y0)，由题可知

则d1=-y0，可求得直线BC方程为因为点P(x0,y0)和原点(0,0)在直线的同一侧，由所以

要求 SΔPAB+SΔPBC的最大值，只要求 t= 3 x+3y的最小值。t= 3 x+3y可化为

（3）不等式法

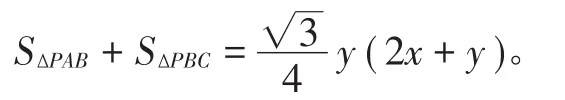
在三角形PAB中，有AB=1，∠APB=120°，由余弦

定理可得+x2+y2+xy=1即

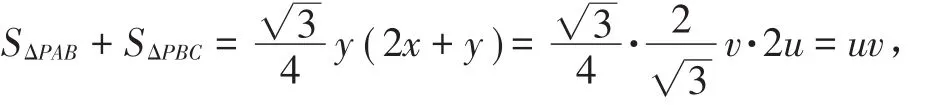
三、问题与思考

（一）参赛教师解题和答辩存在的问题

计算失误。如用三角法求最值时，设∠PAC=θ，将边PA所对的角看成了120°-θ，恰好算出来PA=与正确答案θ)一致，歪打正着。试想解题当中，教师都能出现这种问题，那么在教学中，如何提醒学生规避此类不必要的错误？

分析题目思路高度不够。多数教师只想到了一种方法求解，在思路拓展的时候只有少数教师能想到两种方法，对题目的本质没有把握到位，只停留在问题的表层，教师如此，教学如何指导学生一题多解，甚至多题一解呢？

数学核心素养点拨较少。教师分析题目的时候，重难点都能有效突破，基本方法以及数学思想也有涉及，但是涉及数学学科的核心素养谈得较少，也就是站的角度还不够高，对于学生日后的学科素养培养以及调动他们主动应用数学解决问题的能力不足。

（二）初、高中知识衔接存在的问题

参赛的教师都是高中教师，要么三角法，要么解析法，没有选手用初中的平面几何法，在赛后的分析讨论中，才有教师提出平面几何法：

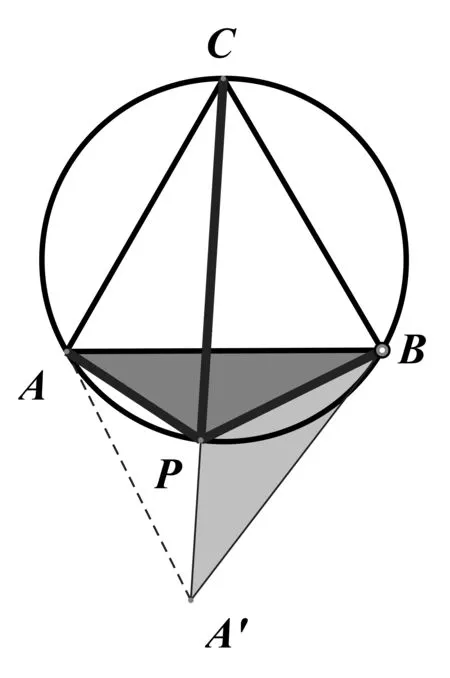
在求SΔPAB+SΔPBC最大值时，由图形发现两个三角形有重叠部分，可以考虑用割补法将两个三角形拼在一起。（图2、图3、图4）BC所成的角相等，均为60°。所以当 PP′为外接圆直径，即的 时 候 ，S四边形PBP′C最 大 为即 S+

图2

图3

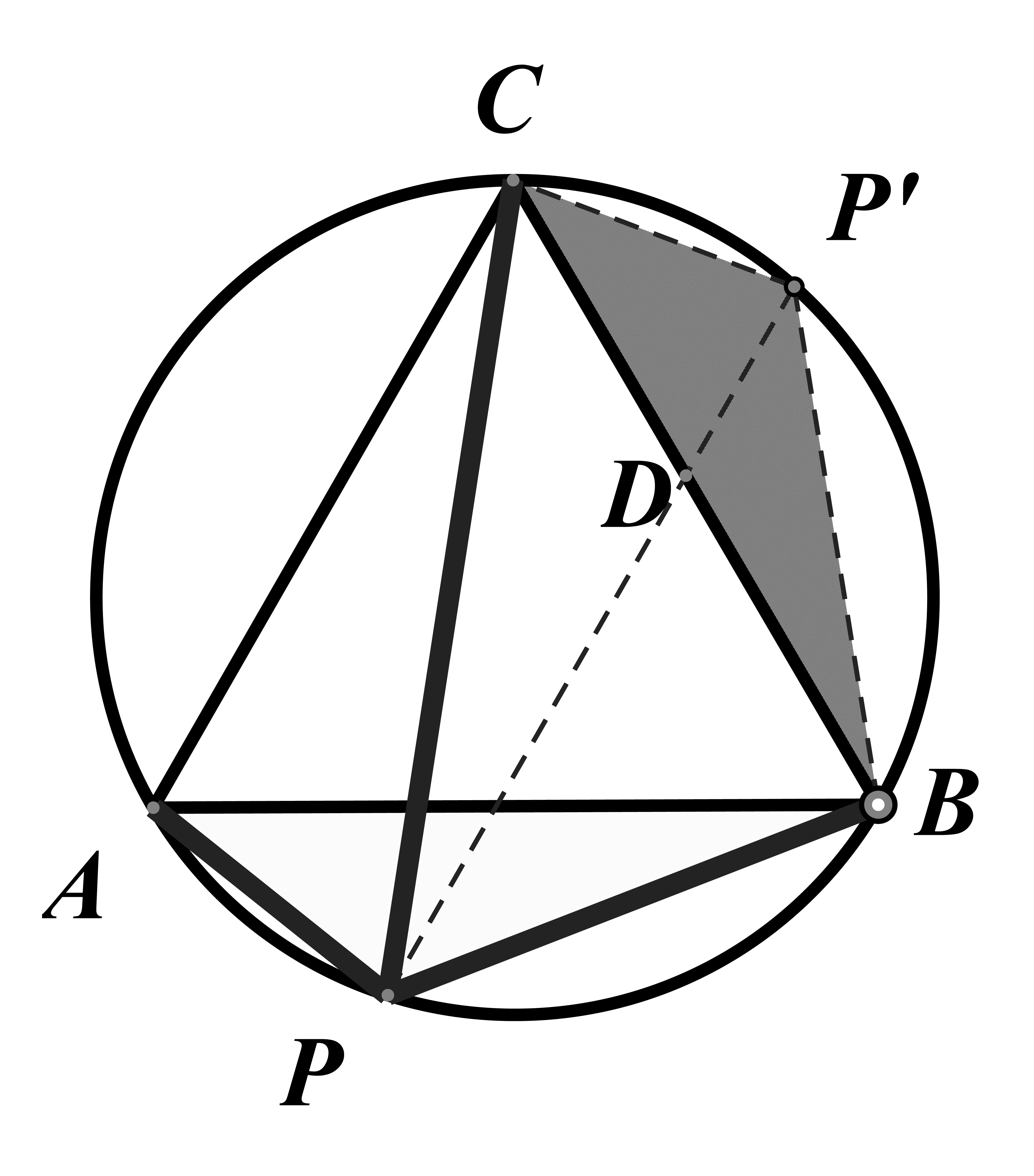
图4

ΔPAB

SΔPBC最大值为解答如下：

法一：设点O为三角形ABC外接圆圆心，连接BO，作点P关于直线BO的对称点P′，根据圆的对称性可知 点 P′一 定 在 圆 周 上 ，连 接 CP′，BP′，显 然ΔBCP′≅ ΔBAP（也可以在劣弧 BC上取一点P′，使得BP′=BP，也可以证明ΔBCP′≅ΔBAP）。此时 SΔPAB+SΔPBC=SΔP′CB+SΔPBC=S四边形PBP′C，可以证明 AC//PP′。在四边形PBP′C中，对角线PP′和BC所成的角与AC和

导致这一问题的原因主要是教师惯性思维，教学方法固化。

（三）教师解题能力对学生数学核心素养培养的影响

提高学生数学核心素养，首先要提升教师的数学核心素养。数学教师除了需要数学概念、法则等命题性知识，“知道怎样做”的实践性知识比“知道是什么”的命题性知识更重要，［1］问题解决是数学教学的核心。［2］教师的解题能力对学生解题能力的影响是正相关的，教师解题的模式化，也会束缚学生的思维，教师的计算能力也直接关系学生的计算速度和质量。学生的学科核心素养的培养在于教师的引导，只有教师的学科核心素养达到一定的高度，注重平时课堂的渗透，才能让学生的核心素养真正得到提升。这道教师技能大赛试题，将问题语言转化为图形语言，通过观察分析，最终通过引入角度或者建立直角坐标系，建立三角模型，利用解三角形和三角恒等变化，最终利用三角函数的有界性求出最值，里面包含了直观想象、逻辑推理、数学建模以及数学运算的核心素养。这种包括解题、析题的比赛，能让教师在平时的解题以及上课中，会多花时间去挖掘题目中所蕴含的基本知识、基本方法以及核心素养，对于提升教师的素养有很大的促进作用，对于培养学生的核心素养也有积极意义。

（四）提高教师解题能力的几点建议

1.关注初高中衔接知识

目前多数学校的人事安排中，多数高中教师只从教于高中学段，极少数人有初高中大循环的经历，多数高中教师对初中学段的学情并不了解，从而在平时教学过程中遇到题目时，就会惯性地把高中知识的解法摆在首位，较少去考虑题目中蕴含的初中就能处理的方法或性质，甚至直接忽略。本次解题大赛中，所有选手都没有提及本题的平面几何解法，可见一斑。而在新课程改革下，初高中衔接问题凸显，如韦达定理、初中平面几何等知识的弱化，导致高中学习过程中经常遇到概念不清导致无法顺利完成解答，若高中教师不能熟练解决初中问题，又如何帮助学生扫除这类解题障碍？

2.学习解题理论提高解题高度

解题是数学教师的立足之本，要想成为解题能手，平时应自觉学习一些数学解题理论，寻找理论支撑。如波利亚的《怎样解题》《数学猜想》《数学发现》等经典著作。罗增儒教授认为，学习数学有三个层次：简单模仿—反复训练—自发领悟。［3］作为教师，更应该变“自发领悟”为“自觉领悟”，并寻找到“自觉领悟”可操作的方法，才能指导学生提高解题能力。教师在解题过程中，应从解题思想、解题目的、解题过程、解题方法、解题原则、解题策略等方面进行深入思考，提高解题高度，而不是只停留在把题目解出来这个层面。对数学本质理解的深度和数学思想掌握的高度是开阔数学解题眼界和视野的基石。［4］

3.限时解题乐当“学生”

部分教师因为平时事务繁忙、或者家庭压力等原因，在备课解题时过度依赖已有答案，倘若经过一小段时间思考还无思路，要么就习惯性翻开答案看看，要么就用拍题软件寻找速成结果，并未深入思考学生解题时有何困难，难点如何突破；更不用说研究题目的内涵与外延，一题多解或多题一解了。教师在平时应保持持续的解题热情，善于解决一些与高考难度相当甚至竞赛难度的题目，学校教研部门可以定期组织教师进行限时训练或解题比赛，教师自己也可以在平时大考中与学生进行同步“限时考试”，在这样的真实模拟考试环境中不断经历解题过程，积累面临难题的解题心理体验。在解完题目后应适当回顾与总结：这样解正确吗，为什么这样解？这样解是普适的吗，有没有更好的解法？解题中用到了什么知识？融汇了什么数学思想方法？这样的题目是否可以进行推广？自己可以命制出类似的题目吗？有没有跟题目类似的一般性结论？……只有真正体会学生的难处，方能为学生提供解决困难的方法和途径，也只有如此才能深化对数学知识的理解、促进自己思维结构的优化，提高解题水平。