经验模态分解在直流电动机性能测试中的应用研究
2018-08-31董袖青张俊晶宫鹏飞朱国威
□ 董袖青 □ 张俊晶 □ 宫鹏飞 □ 朱国威
1.长安大学工程机械学院 西安 710064
2.西安交通大学机械工程学院 西安 710049
1 研究背景
直流电动机换向是一个复杂的机械、化学和电磁过程,由于直流电动机换向和反向电动势脉动原因,直流电动机电枢电流的电气参数包含转速和转矩信息。采用电枢电流的电气参数间接求出直流电动机的转速和转矩特性,具有一定意义。由于直流电动机从静止到稳定转速是一个动态过程,电枢电流信号是一个非平稳信号,因此采用传统傅里叶变换只能分析直流电动机的稳定运行特性。若采用小波消噪、滤波、重构的方法,能够提取出高频分量,但在直流电动机信号采集时会引入高频噪声。采用小波理论滤除高频噪声时,一旦分解层数确定,多分辨率就恒定不变,缺乏自适应性,而且采用不同的小波基,分解的结果差异较大[1]。
经验模态分解(EMD)从信号自身特征时间尺度出发,得到固有模态,整个分解过程体现了多尺度的自适应滤波特性,非常适用于非平稳、非线性过程。文献[2]提出了基于快速博里叶变换(FFT)和 EMD的直流电动机换向电流信号提取方法,通过对前几阶固有模态函数(IMF)分量进行FFT,得到相应的频谱特性,进而通过求出高频电枢电流的瞬时频率,得到直流电动机的转速。但是,将部分IMF分量视为噪声而滤除,会使试验提取的直流电动机转速结果产生偏差。在测试永磁直流电动机的电磁转矩方面,文献[3-4]均采用电磁转矩与转速平衡方程式来求取电磁转矩,对启动阶段电动机的空载阻尼转矩忽略不计。综合上述文献,直流电动机在转速和转矩测试方法方面均存在缺陷。
2 EMD原理
在实际应用中,直流电动机的信号大部分由非线性和非平稳信号组成,信号中包含了多种振荡模式。为了能将各振荡模式从原始信号中分离出来,黄锷提出了一种自适应的信号分析方法,即EMD,并将一系列振荡模式定义为IMF。IMF分量必须满足两个假设条件[5]:① 在信号序列中,过零点和极值点数目必须相等或最多相差1;② 由局部极大值构成的包络线与由局部极小值构成的包络线关于时间轴局部对称。
在IMF分量满足上述假设条件的情况下,任意信号可以经EMD分解为有限个IMF分量和一个余项之和的形式。
EMD的步骤如下。
(1)确定原始信号的所有局部极大值和极小值点,采用三次样条曲线将所有极大值点连接为信号的上包络线,同理将所有极小值点连接为信号的下包络线,求取上包络线和下包络线信号的均值m1(t)。
(2) 原始信号x(t)减去m1(t),得到新的信号h1(t),如果信号h1(t)满足上述 IMF 分量的假设条件,则h1(t)就为第一个 IMF 分量。
(3)通常情况是上述h1(t)不满足 IMF分量的假设条件,因此需要将h1(t)作为原始信号重复进行k次第(1)步和第(2)步,直至h1k(t)满足 IMF 分量的假设条件,所得到的均值趋于0为止,这样h1k(t)就成为第一个IMF分量。

(4) 令c1(t)=h1k(t),原始信号x(t)减去c1(t),得到g1(t)。 将得到的g1(t)作为原始信号,重复进行第(1)步、第(2)步和第(3)步,这样就可以得到第二个 IMF分量c2(t)。重复循环n次,就可以得到原始信号的n个IMF分量,于是有:
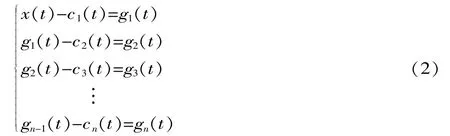
当gn(t)满足给定的终止条件,一般为gn(t)成为单调函数,循环结束,这样原始信号x(t)就可以表示为:

可见,可以将原始信号分解为n个IMF分量和一个残余函数gn(t),其中gn(t)代表信号的平稳趋势。
3 直流电动机启动特性理论
直流电动机的直流电枢电流上会叠加一个高频电流分量,这一分量的频率f应满足:

式中:c为换向片数量;n为直流电动机转速;p为直流电动机磁极对数;m由c的奇偶所决定,当c为奇数时,m=2,当c为偶数时,m=1。
同时,直流电动机的电磁转矩Tem与电枢电流Ia应满足[6]:

式中:Kt为直流电动机的转矩常数;b为电枢线圈并联支路数;N为直流电动机线圈匝数;φ为每极的磁通。
对于每一台已经制成的直流电动机,其b、N、p是确定的,在一定温度下,直流电动机的磁通基本上不随负载变化而变化,因此可以认为Kt为常数[7],只要能够提取出电枢电流的基波分量,就可以计算出直流电动机的电磁转矩。
4 试验采集系统
试验采集系统由永磁直流电动机、非接触式电流传感器、数据采集卡、计算机及外围电路组成。永磁直流电动机型号为 WS-38ZYT64-R,其c=8,p=1。Kt约为0.021 6 N·m/A,数据采集卡采用8通道M1-7008数据采集与分析仪,直流电动机空载启动时所采集的电枢电流时域图如图1所示,采样频率为10 240 Hz。
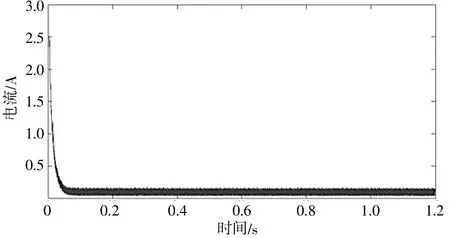
▲图1 直流电动机启动时电枢电流时域图
5 EMD的应用
5.1 电枢电流EMD结果
对采集到的电枢电流信号进行EMD[8],得到的各阶IMF分量如图2所示。
通过对原始电枢电流信号进行FFT,得到其频谱,如图3所示。由图3可知,在低频段,频率634 Hz时的振幅最大,其次是1 268 Hz时的振幅。将已知的直流电动机空载转速、磁极对数和换向片数量等参数代入转速与频率计算公式,可推算出理论上稳态时叠加到电枢电流的高频分量频率为667 Hz,由此可知,634 Hz是这一电枢电流稳态时叠加的高频分量频率,而1 268 Hz则为附加的换向电流频率。由图2可知,IMF1~IMF4主要包含了高频分量,IMF5为频率较低的交流信号,IMF6~IMF10为频率较低的基波分量,将IMF5~IMF10相加,可以得到电枢电流的基波分量。应用FFT对IMF1~IMF4进行频谱分析,得到对应的频谱,如图4所示。由图4可知,IMF1中包含了高于频率634 Hz的高频噪声信号和附加换向电流信号,同时也包含了直流电动机启动阶段的信号;IMF2主要包含了稳态运行时频率为634 Hz的换向电流和频率为1 268 Hz的附加换向电流;IMF3和IMF4包含了直流电动机启动阶段的低频信号和部分噪声信号。通过式(5)计算得到直流电动机的电磁转矩时间关系曲线,如图5所示。由图5可知,直流电动机在启动阶段,电磁转矩在极短时间内增大到最大值,然后在反电动势的作用下,电枢电流逐渐减小到稳定值,此时直流电动机的电磁转 矩 与 空 载 转 矩 平 衡[9],实现了直流电动机的稳定运行。

▲图2 EMD各阶IMF分量
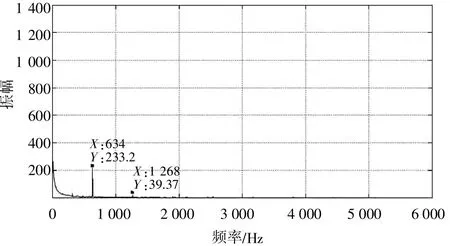
▲图3 原始电枢电流信号频谱
5.2 高频电枢电流小波阈值消噪和滤波处理
通过上述分析可知,将 IMF1~IMF4 相加,得到含噪声和附加高频分量的换向电流。首先采用小波阈值进行消噪,然后对消噪后的高频分量进行巴特沃思低通滤波,通带截止频率为 650 Hz,消噪和滤波后的高频电枢电流如图6所示。由图6可知,消噪和滤波处理后滤除了直流电动机启动阶段的高频噪声信号,同时保留了启动阶段的有效信号。
5.3 高频电枢电流瞬时频率提取及转速特性
直流电动机在启动过程中,转速不断变化,笔者采用小波脊线的方法[10]求 取 消 噪 和 滤 波 后高频电枢电流的瞬时频率。 根据式(4),电动机转速与信号频率成正比关系,可以得到直流电动机的空载转速时间关系曲线,如图7所示。图7与直流电动机理论特性曲线完全相符。图7中,直流电动机空载转速为 4 757 r/min,通过试验可以测得这一直流电动机的空载稳定转速为4 770 r/min,相对误差为 0.272%,证明笔者方法具有较高的测试精度。
6 结论
笔者基于EMD对直流电动机原始电枢电流进行分解,结合FFT的频谱特性,合理选择IMF分量,有效提取出了电枢电流的高频分量和基波分量。采用小波阈值消噪和滤波对提取出的高频分量进行处理,滤除附加的高频分量和噪声信号,完整地保留了直流电动机启动阶段的有效信号。根据提取的电枢基波分量和高频分量,获得直流电动机的电磁转矩和转速参数。试验结果表明,由笔者方法得到的永磁直流电动机机械特性曲线与理论特性曲线相符合。

▲图4 IMF1~IMF4的频谱

▲图5 直流电动机电磁转矩时间关系曲线

▲图6 消噪和滤波后高频电枢电流
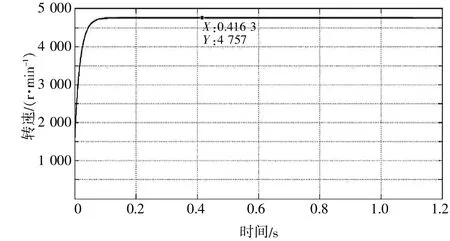
▲图7 直流电动机空载转速时间关系曲线
