把握特征与本质，优选方法构函数——以一道几何动点问题为例

☉苏州高新区实验初级中学 张 萍

一、考题呈现，思路突破

1.考题呈现

（2018年江苏宿迁市中考卷第28题）如图1所示，在边长为1的ABCD中，动点E、F分别位于边AB、CD上，将正方形ABCD沿着直线EF折叠，使点B的对应点M始终落在边AD上（点M不与点A、D相重合），点C落在点N处，MN与CD相交于点P，设BE=x.

（2）随着点M在边AD上的位置发生变化，△PDM的周长是否会发生变化？如若变化，请说明理由；如果不变，请求出该定值.

（3）假设四边形BEFC的面积为S，试求S与x之间的函数表达式，并求出S的最小值.

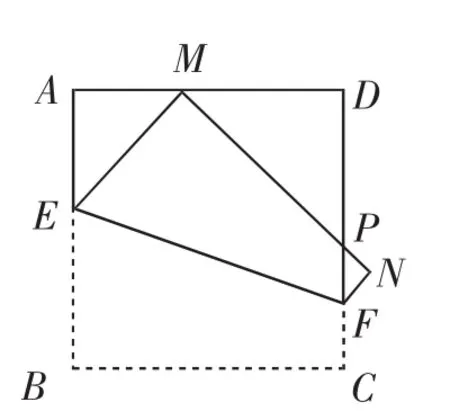
图1

2.思路突破

分析：本题目为常见的几何动点问题，问题涉及到了几何动点的长度、周长和面积等，求解需要借助基本图形的性质.（1）因BE=x，则AE=1-x，求x的值可以将其放在Rt△AEM中，利用勾股定理来构建关于x的方程，通过解方程的方式求x的值.（2）点M为AD上的不确定点，判断△PDM的周长是否会发生变化，可以将其周长表示出来，利用几何性质对其周长所涉及到的线段长进行转化，从而确定其值，然后进行分析.（3）四边形BEFC为直角梯形，可以利用梯形的面积公式，（FC+BE）·BC，可知只需用含有x的参数分别表示出BE、FC的线段长度即可.

解：（1）因BE=EM=x，则AE=1-x，在Rt△AEM中，AM2+AE2=EM2，则）2+（1-x）2=x2，解得x=.

图2

（2）连接BM，BP，过点B作MN的垂线，垂足为点H，如图2，根据条件可以证明△ABM≅△HBM，所以AM=HM，AB=BH=BC，可证△BHP≅△BCP，所以HP=PC，△PDM的周长=MD+DP+MP，其中MP=MH+HP=AM+PC，则C△PDM=MD+DP+AM+PC=AD+DC=2，所以△PDM的周长不会发生变化，为定值2.

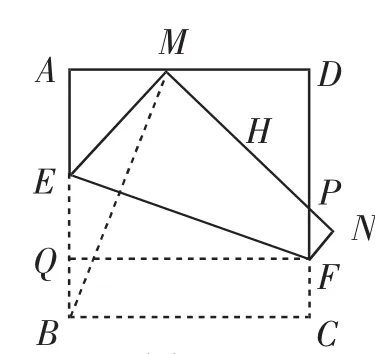
图3

（3）过点F作BC的平行线，与AB相交于点Q，连接BM，如图3，根据折叠的特性可知∠QFE=∠ABM，AB=QF，∠A=∠EQF，分析可知△ABM≅△QFE，所以AM=QE，设AM=a，在Rt△AEM中利用勾股定理可得（1-x）2+a2=x2，解得，AM=QE=，则.S四边形BEFC=（FC+BE）·BC=代入上述函数表达式可得：时，S取得最小值，最小值为.

3.考题评析

本题目属于数学中的动点变化问题，问题涉及到了线段、周长、面积的求值，是对学生综合分析、解题能力的考查.该类问题的显著特点是以点的运动为基本条件，给出了点运动产生的一个或多个变量，要求学生分析几何变量之间关系以及图形运动情况，包括线段长度、角度变化、图形形状、几何面积等.其中较为特殊的问题是建立关于运动变量的函数表达式，表面上属于简单的函数问题，实际上是依托动点，研究几何性质，如上述考题的第（3）问，要求建立面积S关于x的函数关系，并分析S的最大值，形式上属于函数问题.但考虑到面积公式需要求解几何线段，而线段长度的获得离不开几何关系的分析，因此实质上还是几何性质的分析题.本题目所求图形为含有直角的特殊梯形，利用梯形的面积公式可以直接建立关于几何线段的面积函数，简单转化可建立关于动点参数的二次函数，通过代数分析的方式来求解梯形面积的最大值，是几何数形结合思想与方程思想的综合利用.

二、考题衔接，解法探究

建立几何动点中的面积函数是数学常见的考题，上述考题第（3）问所涉及几何图形为具有直角的梯形，因此可直接利用面积公式来完成，该种思路并不具有一般性，如若图形为一般的几何图形，则难以直接利用公式求解，需要合理的对问题模型进行转化，现对其求解策略进行深入探讨.

1.关于面积关系的转化

对于一般图形的面积函数建立，有时可以依据几何性质，建立一般图形与特殊图形的面积关系，如对于具有共同高的几何图形，可以依据图形底的几何性质进行等面积转化，然后通过分析已知图形的线段关系来建立函数解析式.

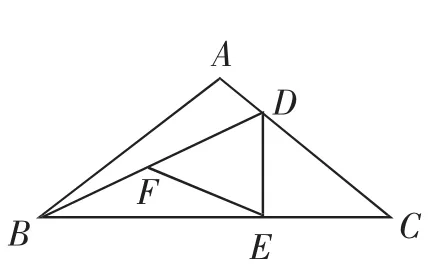
图4

例1 （2018年山东泰安市中考卷第16题）如图4所示，在△ABC中，AC=6，BC=10，tanC=，点D是AC边上的动点（不与点C相重合），过点D作DE⊥BC，垂足为点E，点F是BD的中点，连接EF，设CD=x，△DEF的面积为S，则S与x之间的函数关系式为__________.

分析：问题求解动点的面积函数解析式，需要建立△DEF的面积与线段x之间的关系，由于△DEF为一般的三角形，无法直接利用面积公式，对于△DEF的面积求解可以以DF为底，构建其底上的高，考虑到点F为线段BD的中点，若△DBE以BD为底，则与△DEF具有相同的高，两者之间的面积关系为则只需求解△DBE的面积即可，而对于△DBE可以利用BC边上的垂线DEBE·DE，后续只需研究BE、DE与CD的关系即可.

上述考题求解一般图形的面积采用的是面积大小关系的转化，即利用线段的中点性质，建立待求图形与特殊图形的面积关系，然后利用动点建立的线段参数表示求面积所涉及的线段长，整个过程思路清晰，构思巧妙，对于规则的一般图形面积求解有一定的参考价值.

2.利用面积割补的转化

而对于一般的不规则图形，不仅没有可利用的面积公式，而且难以直接进行面积转化，此时则可以考虑采用面积割补的方式将其转化为几个规则图形的组合，然后利用规则图形的面积公式，建立线段长度关于动点参数的关系，间接获得几何面积的函数解析式.

例2 （2018年山东青岛中考卷第24题）已知：如图5所示，在四边形ABCD中，AB∥DC，CB⊥AB，AB=16cm，BC=6cm，CD=8cm，动点P从点D开始沿着DA边作匀速运动，动点Q从点A开始沿着边AB作匀速运动，它们的运动速度均为2cm/s.点P和点Q同时出发，以QA、QP为边作平行四边形AQPE，设运动的时间为t（s），0＜t＜5.请根据题意回答下列问题：

（1）用含有t的代数式表示AP；

（2）设四边形CPQB的面积为S（cm2），求S与t的函数关系式.

分析：（1）t表示的是点的运动时间，可以用距离公式来表示AP；（2）求S与t的函数关系式，实际上就是用时间t表示四边形CPQB的面积，由于CPQB不规则，可以采用面积割补的方式，利用规则图形表示其面积，如SCPQB=SABCDS△PDC-S△PQA，然后分别用t表示分割后图形的面积即可.

解：（1） 可得AD=10，PD=2t，AP=AD-PD=10-2t.（2）SCPQB=SABCD-S△PDC-S△PQA，过点P作PM⊥AB于M.延长MP、CD交于点N，则四边形NMBC为矩形，∠N=90°，则AQ·PM，其中NP=t，AQ=2t，PM=6-t，所以×（8+16）×6-

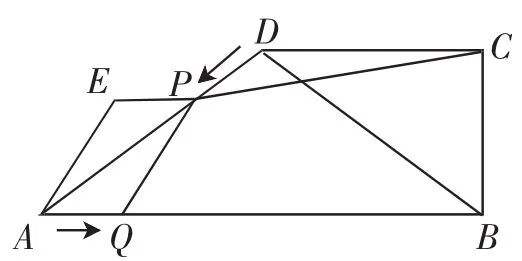
图5

本题目所求四边形为不规则四边形，无法利用面积公式来直接建立关于时间参数的面积函数，解题过程采用面积割补的方式来构建四边形，然后分别建立图形面积关于时间参数的函数.需要注意的是在求解线段长时要合理利用几何性质，如线段垂直、角平分线等.

求解几何动点的面积函数需要利用面积公式，将面积转化为线段关于动点参数的函数，转化的方法与所求图形的形状有着直接的关系，即形状决定解法，对于特殊的图形可以采用直接求解的方式，而对于一般的三角形则可以采用面积关系法，不规则图形则可以采用面积割补的方式，利用规则图形的面积函数来完成.

三、解后思考，总结感悟

几何动点的问题类型很多，其中构建面积函数的表达式是其中较为特殊的问题，由于动点的存在，图形的形状呈现多样性，打开问题的突破口是构建基本解题框架的关键，需要把握问题特征，挖掘问题的本质，结合有效的思想方法及构建方式来完成.

（1）问题特征：对于动点问题的特征提取，需要从点的运动形式以及问题条件来看，求面积需要已知边长，则需要将运动参数转化为线段长度，因此需要注意提取问题中的运动参数，并确定点的运动轨迹.

（2）问题本质：动点函数表达式求解题，虽然从形式上看属于函数问题，但考虑到求解过程需要已知几何的线段长度，因此需要分析几何的关系，因此依然属于几何性质、关系的分析题，求解的关键是构建线段长度关于运动参数的关系，该过程离不开几何性质的利用.

（3）求解思想：该类问题的解题过程实际上是依托转化思想来对问题和条件进行的转化，即转化已知问题形式，联系已知条件，在此基础上利用方程思想来构建函数的表达式，建立两个变量之间的关系，并考虑变量的取值.

（4）解题方法：对于不同的问题条件需要采用对应的解题方法，其中直接求解、面积关系、面积割补是其中常用的方法，方法选取得当可以极大的提高解题效率，需要注意的是方法的选取要结合点的运动情况.

动态面积函数表达式求解题虽然相对较为复杂，但可以遵循一定的解题策略，即首先分析图形特征，确定运动规律；然后转化问题条件，探寻几何关系；最后求解线段长度，构建关于面积函数的表达式.动态几何问题是对知识与能力的多重考查，求解过程不仅是知识的综合利用，还需要调动思维，结合思想方法来探究，因此巩固基本知识，建立知识联系，强化解题思想是学习的关键.