探究几何新定义，形成解题新策略——以一道中考几何新定义题为例

☉江苏省清江中学 张绍俊

一、考题呈现

考题 （2018年江苏淮安中考卷第26题）如果三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”.

（1）如果△ABC是“准互余三角形”，∠C＞90°，∠A=60°，那么∠B=__________.

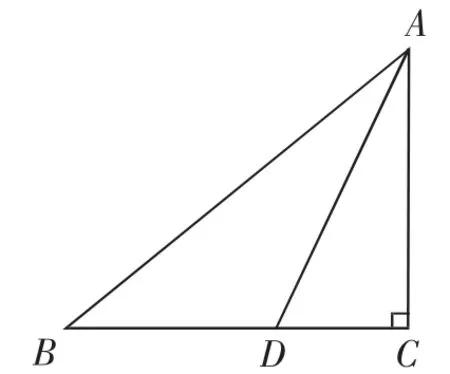
图1

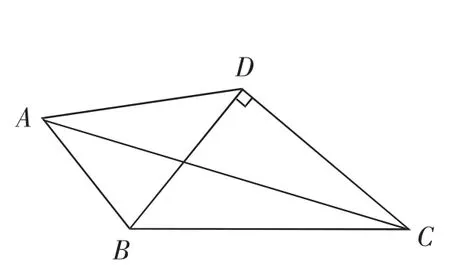
图2

（2）如图1，在Rt△ABC中，∠ACB=90°，AC=4，BC=5，如果AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”；试问在边BC上是否存在一点E（异于点D），使△ABE也是“准互余三角形”？如果存在，请求出BE的长；如果不存在，请说明理由.

（3）如图2，在四边形ABCD中，AB=7，CD=12，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长.

二、思路突破

第一步：理解新定义

在问题分析求解之前，必须先对问题所涉及到的几何定义进行直观理解，“三角形的两个内角α与β满足2α+β=90°”，以图3所示三角形为例，如果2∠A+∠B=90°或者2∠B+∠A=90°，那么△ABC可称之为“准互余三角形”.依据三角形内角和等于180°可知：如果存在关系“2∠A+∠B=90°”，那么∠A必须小于45°，∠B小于90°；如果存在关系“2∠B+∠A=90°”，那么∠B必须小于45°，∠A小于90°，两角必须均为锐角.这样结合具体的图形可以充分理解问题中所陈述的新定义，有利于后面的思路分析与突破.

图3

第二步：问题总体分析

基于上述对于定义的理解，对于问题（1）可知，由于∠C＞90°，∠A=60°，如果△ABC是“准互余三角形”，那么只可能存在一种情形，即2∠B+∠A=90°（∠B＜45°），代入角度即可求解.对于问题第（2）问，探求点E是否存在，可以先假设点E存在，然后分情况来分析，如果点E位于BC边之上，很显然∠AEB＞90°，那么同样只可能存在两种情形，后续只需结合几何性质分析即可.最后一问是在四边形中的△ABC为“准互余三角形”时，求解对角线AC的长，同样需要分两种情况来分析，总体思路是在四边形中分析内角大小，然后根据角的关系构建相似三角形，利用相似三角形边的性质来完成对角线的求解.

第三步：构建突破策略

1.定角突破

第（1）问已知∠C＞90°，∠A=60°，根据定义可知，由于2∠C或2∠A均大于90°，因此只可能存在一种情形：2∠B+∠A=90°，则2∠B=30°，解得∠B=15°.

2.点E确定

由于点E位于BC边上，则∠AEB＞90°，则有2∠B+∠BAE=90°或者2∠BAE+∠B=90°两种情形，但因点E异于点D，则第二种情形不满足.由图4可知，在Rt△ABC中，∠B+∠BAE+∠EAC=90°，又知2∠B+∠BAE=90°，可得∠B=∠EAC，分析可知△ABC∽△EAC，由相似性质可知，=，则EC==，所以BE=.

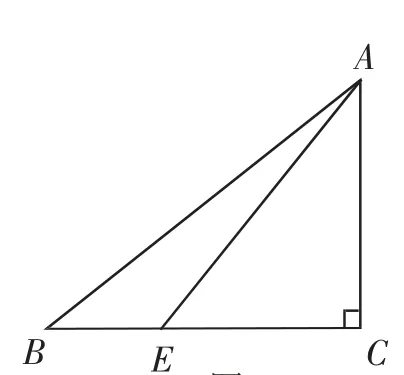
图4

3.对角线AC求解

根据题意可知，∠ABC=∠ABD+∠CBD，∠ABD=2∠BCD，则∠ABC=2∠BCD+∠CBD=90°+∠BCD，所以∠ABC＞90°，存在两种情形，分别进行讨论：

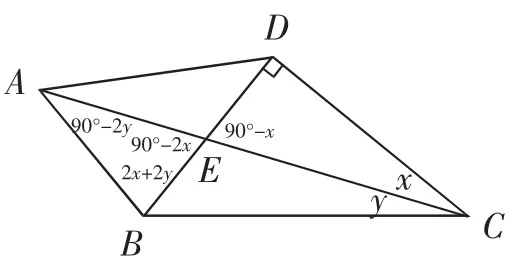
图5

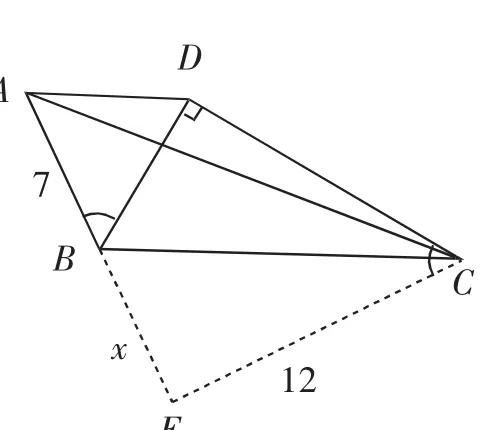
图6

①△ABC是“准互余三角形，∠BAC+2∠ACB=90°，假设∠ACD=x，∠ACB=y，分析可知∠BAC=90°-2y，∠ABD=2x+2y，则∠ABE=90°-2x，如图5，但由于在△AEB中∠AEB=90°-x，则有x=0，与ABCD为四边形相矛盾，故该种情形不存在.

②△ABC是“准互余三角形，2∠BAC+∠ACB=90°，可以从以下两种思路来完成求解.

方法1：半角折叠构建倍角.由于∠ABD=2∠BCD，则可以将∠BCD沿着边BC进行翻折，如图6，则有∠DCB=∠ECB，所以∠DCE=∠ABD，又因为∠ABD+∠DBE=180°，则∠DCE+∠DBE=180°，即∠BDC+∠BEC=180°. 因为∠BDC=90°，所以∠BEC=90°，BC是∠DCE的角平分线，由角平分线的性质可知，CD=CE=12.因为2∠BAC+∠ACB=90°，可设∠BAC=θ，则∠ACB=90°-2θ，∠ACE=90°-θ，即∠ECB=θ，可得△ACE～△CBE，设BE=x，则=，解得x=9，即AE=16，CE=12，在Rt△ACE中使用勾股定理可得AC=20.

方法2：构建导角.

因为2∠BAC+∠ACB=90°，设∠BAC=α，则∠ACB=90°-2α，∠ABC=90°+α，过点B作BE⊥AB交AC于点E，如图7，分析可知△CBE∽△CAB，由相似性质可得CB2=CE·CA.由2∠BCD=∠ABD可得∠BAC=∠BCD，则△BAE∽△DCB，设AE=7a，则CB=12a，可求得CE=9a，所以BE=，利用勾股定理可得AE=7a，所以AC=16a=20，即对角线AC的长为20.

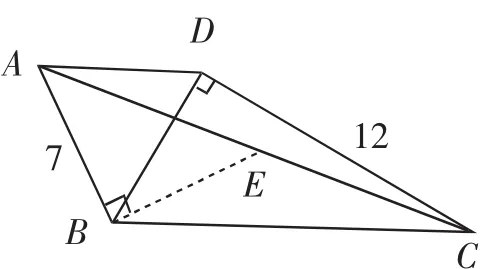
图7

三、考题评析

1.命题评析

本题目为涉及三角形内角的几何新定义题，求解过程需要学生首先理解几何定义，然后运用所学知识来解决问题，是对学生阅读理解、知识运用、方法综合能力的考查.问题的设置具有明显的关联性和递进性，由角到点再到几何对角线，问题层层递进，环环相扣，分析过程由浅入深，由难到易，解法上前者对于后一问的分析具有一定的启示作用，是关联性考题的典型代表.

2.求解评析

新定义考题虽有着较为新颖的命题形式，但依然是基于学生知识基础进行的几何创新，理解定义的核心含义是问题求解的基础，数形结合、模型建立是问题求解的有效方法，基于定义内容，把握知识联系，是构建解题思路的基本策略.上述考题由于三角形内角大小的不确定性，使得新定义的“准互余三角形”具有多种不同形式，因此在分析问题时需要分类讨论，根据角度大小的关系来完成特定情形下的问题求解.考题的第（3）问是本题的难点所在，其解题思路是基于前两问的求解，上述采用了“由角到形，由形入性，以性归质”的分析思路，即首先分析三角形内角关系，确立三角形的形状关系（如全等、相似），然后利用三角形的性质来确定几何线段的长度.求解过程在分类讨论的基础上采用了数形结合、模型构建的方法，而最后一问求解中采用了两种构建策略，一种是利用几何折叠来完成倍角构建，通过角度分析来建立边长求解的代数方程；另一种是在三角形中构建几何导角，同样通过分析内角关系，利用相似性质构建方程求解.其中三角形相似、勾股定理是建立几何关系到代数方程的重要途径，是几何线段求解的基本策略.

四、教学思考

近几年的中考中出现了众多的新定义考题，涉及到了几何概念、代数名称、运算法则、变化规律等，这些优秀的新定义题指引着中考的命题方向，也对中学教学有着重要的引领作用，结合考题分析，指导学生思考，启发学生思维，是考题的价值所在，下面围绕几何新定义考题开展教学反思，探求教学建议：

1.基于新定义，强化阅读理解

给出数学新定义是该类考题最为显著的特征，一般定义中含有大量的文字信息以及必要的数学符号，以描述的方式给出与数学相关的定义.在求解时不应急于思考后续的问题，而应对定义进行文字提炼，并转化为简洁的数学语言，然后构建问题研究的数学模型，充分理解定义所表述的本质内容，这其中涉及到了语言的转化、内容的理解以及模型的构建，对于定义的理解也应分上述三步来完成.因此，在数学教学中十分有必要强化学生概念理解、语言转化的能力，结合数形结合思想指导学生开展数学建模，促进学生数学阅读能力的提升.

2.基于关联性，理解定义内容

中考新定义题的内容虽然与教材的概念定义有一定的差异，但考虑到其命题材料来源于教材，是以学生认知为命题出发点的，因此本质上还是对学生所学概念的一种另类变式.在阅读新定义时可以充分结合教材的知识内容来理解题目定义，包括定义中的数学概念、基本性质和研究方法，思考定义内容与所学知识存在的关联，如上述考题涉及到的“准互余三角形”，就可以联想几何中的互为余角，即α+β=90°，然后明确何种情形下可称之为准互余三角形，进而理解准互余三角形所具有的特征，为后续的分析求解打下基础.

3.基于思想方法，形成分析策略

本文所分析的考题为典型的几何新定义题，求解过程采用分类讨论思想将不确定性问题具体化，然后利用构造思想建立了问题研究的模型，并采用数形结合的方式来分析求解.本文第三问的求解分别采用了不同的构造方式，获得了问题求解的关键条件，正是因为图形的构建使得问题的思考过程更为简洁，这种解题方式是几何问题研究的基本策略.在教学中，不仅应使学生掌握基本的数学知识，还应该渗透思想方法，引导学生掌握问题的分析策略，掌握问题研究的基本方法，逐步形成自我的解题思路，获得解题思维的提升.

五、写在最后

中考新定义题对学生的知识运用能力提出了更高的要求，同时也对初中教学提出了新的目标要求，这是课改推行下的命题导向，也是素质教育的必然趋势.提升学生能力应成为教学的主要目标，包括阅读理解、信息提炼、知识归纳和模型构建能力.使学生获得知识与能力的双重提升，促进学生数学素养的持续发展.