对一道中考模拟题的改编、分析、思考与再编
2018-08-31南京航空航天大学附属初级中学汤晓静
☉南京航空航天大学附属初级中学 汤晓静
近期,在一次中考模拟测试中,笔者对一道模拟试题进行改编,考后受到同行和学生的一致好评,下面对整个过程(改编、分析、思考、再编)进行简单介绍,不当之处,敬请指正.
一、试题呈现
(改编题)如图1,在长方形ABCD中,AB=6,BC=8,点E是对角线BD的中点,点F是边CD上的动点,连接EF,作EG⊥EF交边BC于点G.
(1)若点F是边CD的中点,求EG的长.
(2)当点F在边CD上运动时,∠EFG的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠EFG的值.
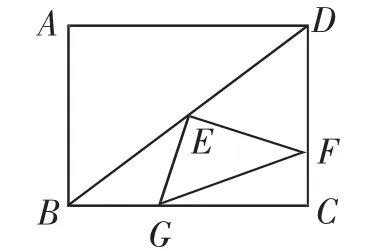
图1
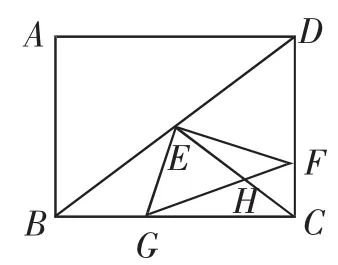
图2
二、改编说明
上述试题是一道改编题,原题以坐标系为载体,坐标原点O与点B重合,边BC、BA所在的直线分别为x轴和y轴,此时AB和BC的长度以坐标的形式给出;原题中对于“点F是边CD上的动点”是这样描述的:点F从点C出发,以每秒1个单位长度的速度在线段CD上移动,设移动时间为t,这样原题中的第(3)问就是“求此时t的值”;原题中第(3)问较难,需要分类讨论,其中是这样给出条件的:当EH将△EGF分成的两部分的面积之比为1∶2时,求相应的t值.笔者认为改编后的试题题干叙述更加简洁、设问更加清晰;学生理解起来更加容易,做题过程中思路也更加开阔,摆脱了平面直角坐标系的限制,解法更加经典、简洁,符合“好题”的命制理念和追求.
三、思路分析
第(1)问:略(主要考查学生对中位线基本知识的掌握).
第(2)问:主要考查学生对“直角”问题处理策略的灵活掌握情况,如图3所示,容易得到△PGE∽△QEF,所以进而tan∠EFG=.运用此题的处理方法,可以轻松解决下面这个题目:
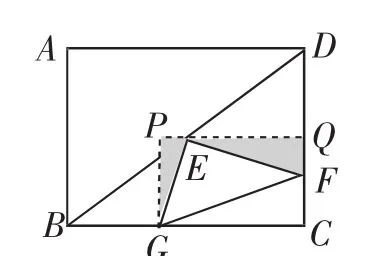
图3
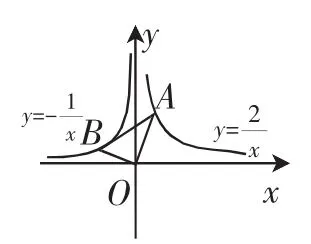
图4
如图4,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数y=-、y=的图像交于B、A两点,则∠OAB大小的变化趋势为( ).
A、逐渐变小 B、逐渐变大C、时大时小 D、保持不变此外,还可以引导学生通过“四点共圆”的视角去理解,易得∠EFG=∠ECG,进而解决问题.
第(3)问:在原题的求解过程中由于平面直角坐标系的存在,大体思路如下:首先容易得到点F和点G的坐标;然后将面积关系转化为线段的比值关系,进而求得点H的坐标;最后利用待定系数法求得线段EC所在直线的方程,再将点H的坐标代入,进而解决问题.
这里我们可以引导学生通过几何的角度去解决问题,通过构造相似将改编题中的转化为(如图5).
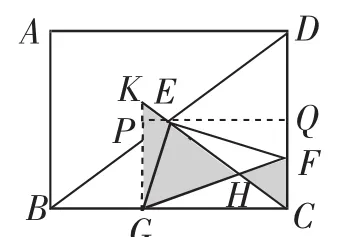
图5
设CF=t,则QF=3-t,根据第(2)问的分析可以得到,进而CG=PQ=EQ+EP=4+,所以KG=
四、两点思考
1.注意对基本图形的考查
通过上面的介绍可以看出,改编后的考题更加重视对初中阶段基本知识和基本图形的考查,涉及到的基本图形主要有三角形中位线的基本图形,相似中的“一线三等角”和“X型图”等,当然每一个基本图形都对应着初中阶段的一个核心知识,应该引起一线教师的足够重视.
2.加大对基本思想的渗透
一线教师在教学中应该利用典型题目,加大对基本思想的渗透.以改编题的第(2)问为例,此处应该渗透函数的思想,引导学生体会通过正切值的不变性是如何说明角度不变的.在第(3)问的求解过程中用到了一系列的转化,首先通过添加辅助线将转化为,然后根据比例关系将求GK的长度转化为求CG的长度,最后将CG的长度转化为PQ(PQ=EQ+EP)的长度,将问题一步一步解决,教学中应该引导学生重点体会如何将未知化为已知.
五、变式再编
再编1:对于此题还可以从下面的角度进行考查:当点F在边CD上运动时,四边形EFCG面积的大小是否发生变化?如果变化,请说明理由;如果不变,请求出该值.
再编2:可以改变∠GEF的呈现形式,引入“旋转”:∠GEF绕直角顶点E旋转,旋转过程中与边CD、BC分别交于点F和点G,其余条件不变.
再编3:可以改变四边形ABCD的形状,比如改为正方形或任意的长方形.
再编4:可以改变点E的位置:点E为对角线BD上的任意一点(不与端点重合).
再编5:可以改变点F和点G的位置:在“旋转”的背景下,可以让点F和点G在边CD和边BC所在的直线上.
下面给出一例:
如图6,在矩形ABCD中,∠ACB=30°,将一块直角三角形的顶点P放在两对角线AC、BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别与边AB、BC所在的直线相交,交点分别为E和F.
(2)如图7,现将三角板绕点P逆时针旋转角度α(0°<α<60°),求的值;
(3)如图8,在(2)的基础上继续旋转,60°<α<90°,再在AC上移动点P,使的值是否变化?证明你的结论.
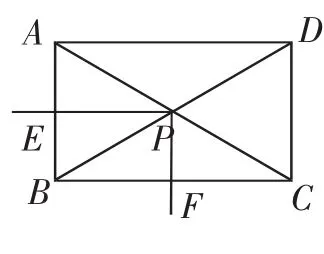
图6
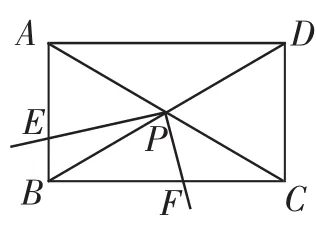
图7
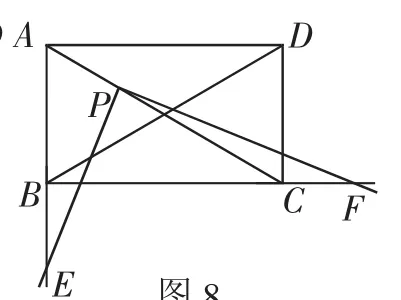
图8
